термодинамика. Основы химической термодинамики
 Скачать 1.12 Mb.
|
|
ОСНОВЫ ХИМИЧЕСКОЙ ТЕРМОДИНАМИКИ Химическая термодинамика – наука о превращениях одних форм энергии в другие (при протекании химической реакции за счет теплового, хаотического движения молекул, атомов, ионов). Химическая термодинамика изучает: - энергетические эффекты, сопровождающие химические реакции; - возможность, направление и предел самопроизвольного протекания химического процесса в данных условиях; - условия равновесия в химических реакциях. Некоторые основные термины и определения Системой называется совокупность находящихся во взаимодействии веществ или частиц, мысленно или фактически обособленных от окружающей среды (последняя также является системой). Система называется изолированной, если она не обменивается с окружающей средой энергией и веществом. Система называется закрытой, если она обменивается с окружающей средой энергией, но не обменивается веществом. Система называется открытой, если она обменивается с окружающей средой энергией и веществом. Фаза – это часть системы, однородная во всех точках по химическому составу и свойствам, и отделенная от других фаз поверхностью раздела, которая, в принципе, может быть выделена из системы каким-либо механическим способом. Гомогенная (однородная) система – однофазная система, любое свойство которой имеет во всех частях одинаковое значение или непрерывно изменяется от точки к точке. Например, жидкая вода, лед, растворы. Гетерогенная (неоднородная) система - система, отдельные части которой различаются по свойствам и отделены друг от друга поверхностями раздела. Примером такой системы может служить лед в воде, туман, суспензия глины в воде. Химическая система - совокупность веществ и частиц, способных к химическому взаимодействию. Термодинамические параметры - величины, характеризующие макроскопические свойства системы. Например, давление, объем, температура. Уравнения состояния - количественные зависимости между параметрами системы. Одним из уравнений состояния является уравнение, описывающее состояние идеального газа (уравнение Менделеева – Клапейрона): рV = nRT. Благодаря уравнению состояния, для однозначной характеристики состояния системы оказывается достаточным знание только нескольких независимых свойств (параметров). Остальные являются функциями параметров и их определение однозначно, если заданы значения других. Если, например, для газообразной системы известны величины T, V и n, то величина р определяется однозначно т.к. р = f (T,V,n). Понятие о функции состояния Химическая термодинамика изучает состояния системы, которые характеризуются ее физическими и химическими свойствами (V, p, T, химический состав и т.д.). В термодинамике систему характеризуют при помощи функций состояния. Функция состояния – величина, определяемая параметрами состояния, однозначно характеризующая систему и не зависящая от пути достижения данного состояния данной системой. Свойства функцийсостояния: 1. Функция состояния системы не зависит от предыстории, т.е.пути достижения данного состояния (температура, объем и т.д.) данной системой (состав, количество). 2. Функция состояния есть величина аддитивная: функция состояния целого (системы) равна сумме функций состояния ее частей. 3. Абсолютное значение функции состояния f определить, как правило, нельзя, но ее изменение (Df) при переходе системы из одного состояния в другое - величина определенная и измеряемая. Примером функции состояния может служить потенциальная энергия. Абсолютное значение потенциальной энергии тела определить нельзя, т.к. оно испытывает притяжение не только Земли, но и Солнца, звезд, галактики и т.д. Однако это не мешает определить изменение величины потенциальной энергии тела DЕ при его перемещении из точки а в точку в. Достаточно правильно выбрать начало отсчета - считать, что в каком-то положении (например, на поверхности Земли) потенциальная энергия равна нулю, и тогда в любой другой точке над этой поверхностью она будет равна mgh независимо от того, каким путем тело туда попало (h- высота над поверхностью Земли). Изменение потенциальной энергии при перемещении из точки а в точку вравно: DЕ = Еа - Ев = mghв - mghв = mgDh. Независимо от траектории тела. Очевидно, что самопроизвольно тело может переместиться из точки а в точку втолько при условии hв < hв (DЕ < 0). Знание неких подобных потенциальной энергии величин f, характеризующих химическую систему в начале (fисх.) и в конце процесса (fкон.), позволило бы предсказать возможное направление химической реакции в определенных условиях. Нахождение таких функций, исследование их зависимостей от условий протекания реакций и использование их для расчета оптимальных условий проведения реакций и составляет предмет химической термодинамики. Внутренняя энергия, теплота, работа Понятие энергии в механике связывают либо с движением тел, либо с положением этих тел в силовом поле. Сохранение энергии рассматривается как постоянство суммы кинетической и потенциальной энергии, при этом не принимается во внимание внутреннее состояние этих тел. Однако движущееся тело имеет не только кинетическую и потенциальную энергии, но и определенную тепловую энергию (температуру). При контакте этого тела с другим телом, температура которого ниже первого, начнется переход тепловой энергии от первого тела ко второму, при этом внутреннее состояние обоих тел изменится, так как меняется запас энергии. С другой стороны, увеличение «запаса теплоты» может быть достигнуто за счет уменьшения кинетической энергии (например, удар пули о твердую поверхность приводит к повышению температуры и поверхности, и пули). Нагретое тело при охлаждении может стать источником механической энергии, что реализуется в тепловых машинах. Внутренняя энергия системы (U) включает в себя все виды энергии системы (кинетическую энергию поступательного, вращательного, колебательного движения молекул и все формы движения атомов, электронов, ядер и т.д.) за исключением кинетической и потенциальной энергии всего тела (системы). Изучение двух последних видов энергии не входит в задачи термодинамики. Как и любую энергию, внутреннюю энергию нельзя измерить. Однако, можно определить ее изменение при переходе из одного состояния в другое. В термодинамике обычно исследуют две формы передачи энергии от одной системы к другой – теплоту Q и работу А. Теплота – неупорядоченная форма передачи энергии, которая переходит путем хаотического столкновения молекул соприкасающихся тел, т.е. путем теплопроводности или теплоизлучения. В термодинамике положительной (Q > 0) считается теплота, подведенная к системе. В термохимии подводимая к системе теплота имеет противоположный знак (Q < 0). Работа – упорядоченная форма передачи энергии, общей чертой которой является перемещение масс, состоящих из очень большого числа молекул, под действием каких-либо сил. Положительной (А > 0) считается работа, совершаемая системой против действия внешних сил. Теплота и работа характеризуют качественно и количественно две различные формы передачи энергии от одной части материального мира к другой. В отличие от внутренней энергии, теплота и работа зависят от способа проведения процесса, т.е. являются функциями пути. Первый закон термодинамики. Понятие об энтальпии Первый закон термодинамики является частным случаем закона сохранения энергии применительно к процессам, в которых выделяется, поглощается или преобразуется тепловая энергия. Рассмотрим, как изменяется внутренняя энергия DU при проведении процесса, в котором система (газ, находящийся при постоянном давлении р = const в цилиндре под поршнем) получает некоторое количество тепловой энергии Qр, в результате чего газ нагревается (Т2 > T1, U2 > U1) и расширяется (V2 > V1) (рис. 1). 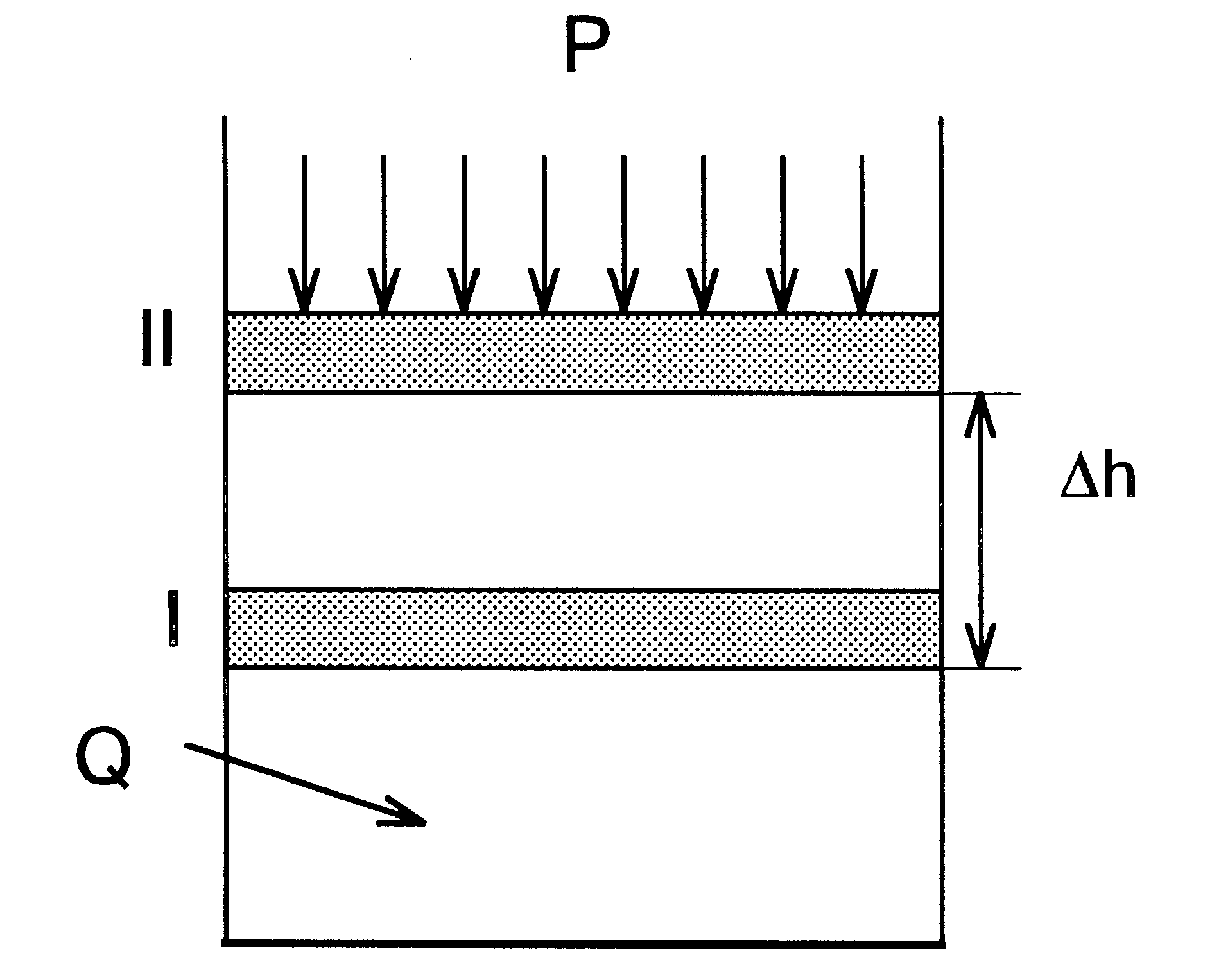 Рис. 1. К выводу первого закона термодинамики Если положение поршня не зафиксировано, то поршень будет перемещаться до тех пор, пока внешняя сила F, приложенная к поршню, не уравновесит силу, действующую на поршень со стороны системы. Тогда имеем F = p.s, где p – внешнее давление, s - площадь поперечного сечения цилиндра. При этом движении совершается работа против сил внешнего давления, равная A = F .Dh, где Dh – величина перемещения поршня. Поскольку произведение площади поперечного сечения цилиндра на величину перемещения поршня есть приращение объема системы DV, то можно записать A = F .Dh = р. s. Dh = p . DV. Таким образом, тепловая энергия (-QР), сообщенная газу, при постоянном давлении (p=const) идет частично на увеличение внутренней энергии DU, а частично на работу расширения A
Сумма внутренней энергии и произведения давления на объем (H = U + pV) получила название энтальпии или энергосодержания. Энтальпия и внутренняя энергия являются функциями состояния данной системы. Если подвод тепла к цилиндру с поршнем осуществлен в изобарных условиях, т.е. при постоянном давлении (p=const) , как это предполагалось при выводе уравнения (2), то -QP = DН. Если закрепить поршень и подвести теплоту при постоянном объеме (  V = const), то V=0, и вся теплота пойдет на увеличение внутренней энергии:-QV = DU. Так как чаще всего реакции проводят при постоянном объеме (например, атмосферном) давлении, далее в расчетах мы будем использовать величину DН. Так как энтальпия является функцией состояния, то все общие свойства функции состояния распространяются и на неё. Свойства энтальпии: 1. Разность энтальпий системы в конечном и начальном состояниях не зависит от пути перехода системы из одного состояния в другое. 2.Энтальпия системы равна сумме энтальпий частей, составляющих систему, т.е. энтальпия - величина аддитивная. 3.Абсолютное значение энтальпии системы (как и абсолютное значение потенциальной энергии тела) является принципиально неопределяемым. Однако, как и в случае с потенциальной энергией, при термодинамических расчетах нас интересует не абсолютные величины энтальпии, а их изменение при переходе системы из одного состояния в другое. Вспомним, что при расчете изменения потенциальной энергии при переходе с одного уровня на другой произвольно выбирают уровень, на котором потенциальную энергию тела полагают равной нулю (не важно, что ниже этого уровня потенциальная энергия тела оказывается отрицательной, так как это не скажется на результате расчета величины изменения потенциальной энергии). Точно также может быть произвольно выбрано единое начало отсчета энтальпии для всех химических систем. Энтальпия любой системы равна сумме энтальпий веществ, входящих в её состав. В свою очередь, энтальпия вещества зависит от его строения, количества, температуры и давления. Следовательно, за начало отсчета для веществ любого строения следует выбрать (произвольно) одни и те же условия (стандартные условия). За точку отсчета принимают значение энтальпии образования простых веществ при 298К (25оС), давлении 101,3 кПа (1атм.), если они при этих условиях, называемых стандартными, находятся в устойчивом состоянии. Стандартные термодинамические величины обозначают определенным образом (например  - стандартная энтальпия вещества А). Невозможность определения абсолютной энтальпии распространяется и на абсолютные величины стандартных энтальпий веществ, поэтому они не могут быть использованы для расчета теплот реакций. Однако для этих целей можно пользоваться относительными величинами, например, величинами энтальпий образования веществ.При этом полагают (это также является произвольно выбранным условием), что любое вещество образуется из простых веществ, каждое из которых находится в стандартных условиях, причем в модификации, устойчивой при этих условиях. В соответствии с этим положением, стандартные энтальпии образования всех простых веществ, устойчивых в стандартном состоянии, равны нулю (например,  ). В скобках указывается агрегатное состояние вещества: тв – твердое, ж – жидкое, г – газообразное. Например,  , а  , что не характерно для натрия в газообразном состоянии при стандартных условиях.Для характеристики энтальпии сложного вещества вводят понятие стандартная энтальпия образования, которая равна количеству теплоты с обратным знаком, выделяющейся или поглощающейся при образовании одного моля вещества из простых веществ, находящихся в устойчивых агрегатных состояниях в стандартных условиях. Размерность энтальпии образования вещества – кДж/моль. Стандартные энтальпии образования большинства сложных веществ имеют отрицательные значения, так как образуются из простых веществ с выделением теплоты. Стандартные энтальпии образования определены для большого количества веществ и сведены в таблицы термодинамических величин (см. Приложение, табл .2). На примере реакции горения метана покажем, почему и как тепловой эффект реакции может быть рассчитан с использованием величин стандартных энтальпий образования веществ CH4(г) + 2О2(г)  CО2(г) + 2Н2О(г) , DНорисходные вещества продукты реакции, где DНр – изменение энтальпии для данной реакции, кДж (при расчете  стандартная энтальпия образования каждого вещества (кДж/моль) умножается на число его молей в соответствии с уравнением реакции).Исходные и конечные вещества могут быть получены из одних и тех же простых веществ С(ТВ) + 2Н2(Г) + 2О2(Г), взятых в одних и тех же количествах С(ТВ) + 2Н2(Г) + 2О2(Г) CH4(г)+ 2О2(г), DН1простые вещества исходные вещества С(ТВ) + 2Н2(Г) + 2О2(Г) CО2(Г) + 2Н2О(Г), DН2.простые вещества продукты реакции Энтальпия – функция состояния, поэтому её изменение в процессах простые вещества продукты реакции, простые вещества исходные вещества продукты реакцииодинаковы (одно из свойств функций состояния): DН2 = DН1 + DНр, где  и  В стандартных условиях:  Разница суммы энтальпий образования продуктов реакции и исходных веществ определяет тепловой эффект (QP) реакции, взятый с обратным знаком (так как DНор = - QР). Рассчитать DНо298,р. для данной реакции можно, пользуясь табличными данными (см. Приложение, табл.2): DНо 298, р = (DНоСО2+ 2 DНоН2О ) - (DНоСН4+ 2 DНоО2) , кДж. DНо 298,р = (DНоСО2+ 2 DНоН2О ) - (DНоСН4+ 2 DНоО2) = = [(-393,5) + 2(-241,8) - (DНоСН4) - 2(0)] кДж = - 802,2 кДж. Для точного расчета теплового эффекта реакции, протекающей в нестандартных условиях (например р = 101,3 кПа, Т 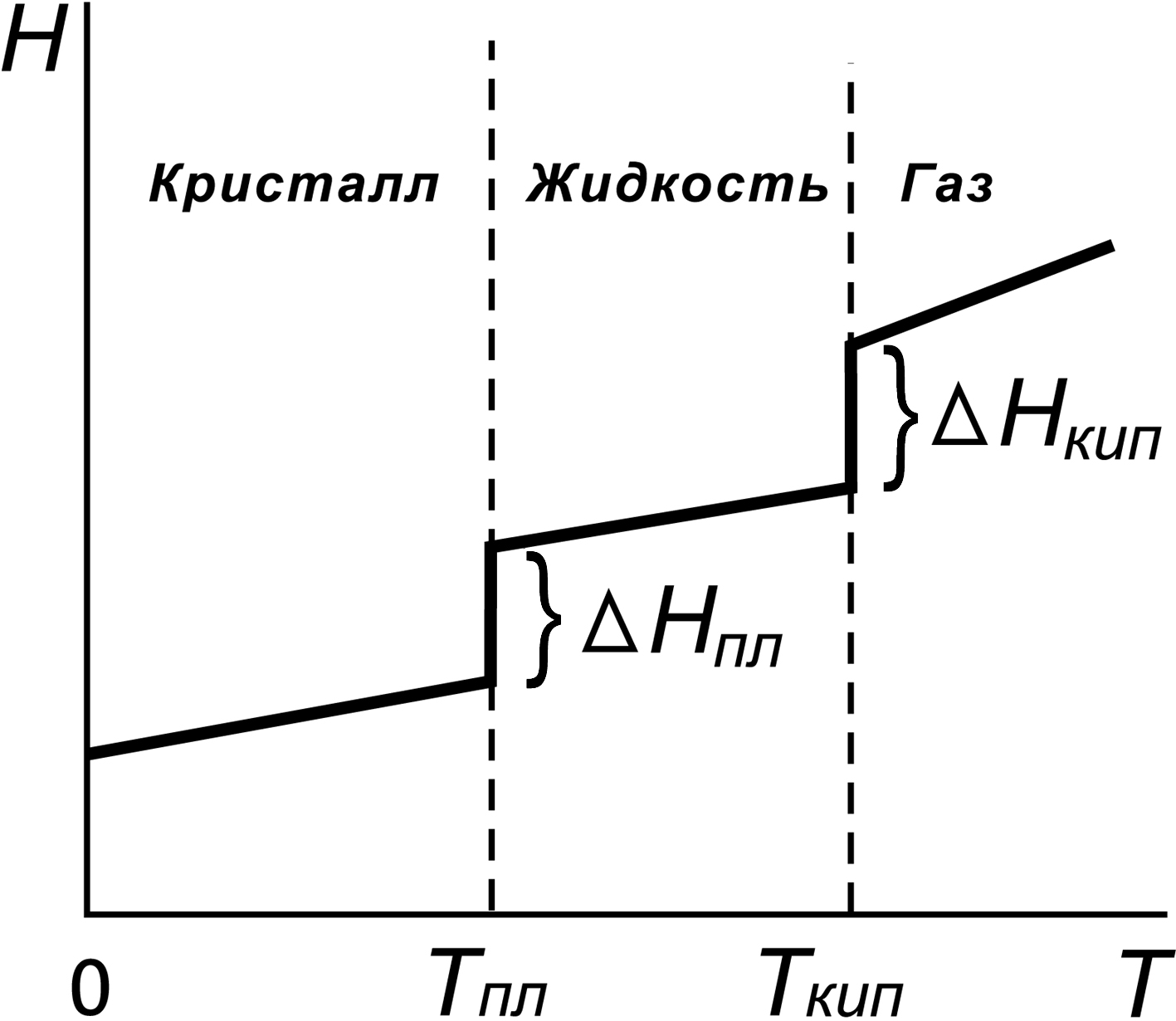 298 К), следует рассчитать энтальпии образования всех участвующих веществ при этих условиях. В общем виде зависимость энтальпии образования от температуры показана на рис.2, из которого видно, что при фазовых переходах изменение энтальпии происходит скачкообразно на величину, соответственно, теплоты плавления ∆Нпл. или парообразования (кипения) ∆Нкип., взятых с обратным знаком. Рис. 2. Зависимость энтальпии образования вещества от температуры В пределах одного фазового состояния (газового, жидкого и т.д.) изменение энтальпии при изменении температуры невелико, поэтому при приближенных расчетах этим изменением пренебрегают. Уравнение температурной зависимости энтальпии моля вещества в пределах одного фазового состояния:  ,где СР – мольная теплоемкость при постоянном давлении, которая равна количеству теплоты, необходимому для нагревания 1 моля вещества на один градус. СР зависит от природы и агрегатного состояния вещества, а также от температуры. Однако в небольшом температурном интервале зависимостью СР от Т можно пренебречь и считать, что DН = СР  DТ. С помощью этого соотношения можно рассчитать энтальпии веществ для различных температур (в пределах одного агрегатного состояния). |