термодинамика. Основы химической термодинамики

• Название: Основы химической термодинамики
• Дата: 12.12.2018
• Размер: 1.12 Mb.
• Имя файла: термодинамика.doc
• Тип: Документы; #59972
• страница: 2 из 7

Тепловой эффект химической реакции
Тепловой эффект химической реакции – изменение энергии системы в результате протекания химической реакции при условии, что система не совершает никакой другой работы, кроме работы расширения.

Если в результате реакции теплота выделяется, т.е. энтальпия системы понижается (DН<0), то реакция называется экзотермической.

Реакция, протекающая с поглощением теплоты, т.е. с повышением энтальпии (DН>0), называется эндотермической.

Тепловой эффект химической реакции при постоянном давлении называют энтальпией химической реакции.

Тепловой эффект, приведенный к стандартным термодинамическим условиям, называется стандартным изменением энтальпии реакции (DН^о_{298, реакции} ).
Термохимические расчеты
Так как изменение энтальпии не зависит от пути протекания, то и тепловой эффект реакции не зависит от того, по какому пути протекает реакция. Это положение было экспериментально установлено Г.И. Гессом в 1840 году и известно как закон Гесса.

Закон Гесса. Тепловой эффект химической реакции зависит от природы и состояния исходных веществ и конечных продуктов, но не зависит от пути реакции, т.е. от числа и характера промежуточных стадий.

Например, процесс окисления углерода С_тв до СО_2(Г) можно осуществить как через стадию непосредственного сгорания углерода до углекислого газа с тепловым эффектом DН (путь I), так и через стадию
+ О_2(Г)

C(тв) СО2(Г) , DН (путь I) + ½ О2(Г), + ½ О2(Г), DН1 DН2, (путь II)

СО_(Г)
образования промежуточного продукта – окиси углерода – СО_(Г) с тепловым эффектом DН₁, с последующим окислением СО_(Г) до СО_2(Г) с тепловым эффектом DН₂ (путь II) в соответствии с уравнениями реакций:

СТВ. + О2(Г) СО2(Г), DН (I) СТВ. + ½ О2(Г) СО(Г), DН1 СО(Г) + ½ О2(Г) СО(Г), DН2 (II) ------------------------------------------- СТВ. + О2(Г) СО2(Г), DН1+ DН2. Из сопоставления тепловых эффектов реакций следует, что DН = DН1 + DН2, т.е. каким бы путем не осуществлялась реакция, ее тепловой эффект будет одинаков, если не меняется конечное и исходное состояния системы. Уравнения реакций, записанные с соответствующим тепловым эффектом, называются термохимическими. В термохимических уравнениях указывается агрегатное состояние вещества. Термохимические уравнения допускают наличие дробных коэффициентов, поскольку они указывают не количество молекул, а количество молей вещества. Согласно закону Гесса с термохимическими уравнениями можно оперировать как с алгебраическими. Закон Гесса позволяет рассчитать энтальпию химических реакций. Энтальпия химической реакции DНо298, реакции равна разнице суммы стандартных энтальпий образования продуктов реакции и исходных веществ с учетом стехиометрических коэффициентов DНо298, реакции = .
В общем случае, для реакции в стандартных условиях аА(Г) + bВ(Г) сС(Г) + dD(Г) DНо298, реакции = [(cDНоC + dDНоD) – (аDНоА + bDНоВ)], кДж, где DНо298, реакции – энтальпия химической реакции, кДж; DНоА, DНоB, DНоC, DНоD – стандартные значения энтальпий образования веществ, участвующих в реакции, кДж/моль; а, b, с, d – стехиометрические коэффициенты в уравнении реакции. Можно также рассчитать значение стандартной энтальпии образования одного из исходных веществ или продуктов, если известны энтальпии образования остальных реагентов и энтальпия химической реакции. Например, для реакции аА(Г) + bВ(Г) сС(Г) + dD(Г), DНо298, реакции > 0. DНоА(Г) = cDНоC(Г) + dDНоD(Г) – bDНоВ(Г) - DНо298, реакции , кДж/моль А(Г).
Зная теплоты образования веществ, можно определить и их теплоты разложения по закону Лавуазье – Лапласа: При разложении сложного вещества на простые поглощается (или выделяется) столько же теплоты, сколько выделяется (или поглощается) при его образовании из простых веществ в тех же условиях. Так, если Н2(Г) +½ О2(Г) ® Н2О(Г) , DНореакции = - 241,8 кДж, то Н2О(Г) ® Н2(Г) +½О 2(Г), DНореакции = 241,8 кДж.

Понятие об энтропии и второй закон термодинамики
Первый закон термодинамики позволяет определить тепловые эффекты химических реакций (но не направление реакций в данных условиях). В 1854 г. датский химик Ю. Томсен, а затем французский химик М. Бертло высказали предположение о том, что химические процессы самопроизвольно идут только с выделением теплоты, т.е. с уменьшением энтальпии системы (с экзотермическим эффектом, ∆Н< 0).

Однако известно много примеров, когда химические реакции самопроизвольно протекают с поглощением теплоты (например, при растворении в воде некоторых солей аммония, таких как NH₄Cl, NH₄CNS) и, более того, одни и те же реакции в зависимости от условий могут идти как в прямом, так и в обратном направлениях. Решить вопрос о направлении химической реакции в данных условиях можно на основании закономерностей, вытекающих из второго закона термодинамики (и, в первую очередь, представления о термодинамической функции состояния, называемой энтропией).
Число микросостояний (термодинамическая вероятность) и энтропия
Тенденция к уменьшению энергосодержания, т.е. уменьшению энтальпии системы, при р = const не является единственным фактором, определяющим направление самопроизвольного протекания реакции в данных условиях.

Вероятно, существуют две движущие силы самопроизвольного процесса: одна стремится уменьшить энергосодержание системы с выделением теплоты, и какая-то вторая сила, в ряде случаев превосходящая первую. Для изучения этой силы рассмотрим процесс смешения двух газов, не реагирующих между собой.

Пусть два инертных газа – гелий и неон – находятся при одинаковой температуре и давлении в двух одинаковых частях сосуда, разделенных перегородкой (состояние 1) (см. рис. 3).

Удалим перегородку, не изменяя энергетического запаса системы. Хотя давление газов в обеих частях сосуда было одинаковым, начнется процесс смешения газов, и через некоторое время молекулы гелия и неона будут равномерно распределены по всему объему системы (состояние 2). Процесс смешения газов, т.е. переход их из состояния 1 в состояние 2, проходил без изменения энтальпии, так как при комнатной температуре какое-либо взаимодействие между молекулами инертных газов практически отсутствует. Газы, разделенные перегородкой (состояние 1), распределены в системе с бóльшим порядком по сравнению со смесью газов (состояние 2).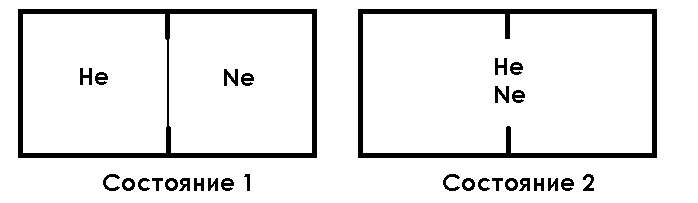


Рис. 3. Процесс смешения газов
По-видимому, движущей силой смешения газов является тенденция перейти в более хаотичное состояние.

В химической термодинамике применяют обычно выражения «беспорядок» или «степень беспорядка», т.е.:
степень беспорядка 2  степени беспорядка 1.
Самопроизвольный процесс, проходящий без изменения энергетического состояния изолированной системы, совершается только в направлении, при котором беспорядок в системе возрастает.

Трудно представить, чтобы два газа, не разделенные перегородкой, не смешались, такое состояние маловероятно. Более вероятное равномерное распределение молекул газа по всему объему. Движущей силой смешения газов является тенденция перейти в более вероятное (хаотичное) состояние.

Самопроизвольный процесс, проходящий без изменения энергетического состояния изолированной системы, совершается только в направлении, при котором система переходит в более вероятное (хаотичное) состояние.

Химическая термодинамика изучает системы реагирующих веществ, состоящие из очень большого числа частиц. В подобных системах различают так называемые макро- и микропараметры. К макро характеристикам относятся независимые переменные, свойственные системе в целом, например, давление, объем, температура.

Макроскопическое (наблюдаемое) состояние системы, характеризуемое определенными термодинамическими параметрами, может существовать при различном распределении молекул, т.е. оно осуществляется разными микросостояниями, отличающимися друг от друга по определенному признаку (например, по координатам x, y, z каждой молекулы в пространстве, скорости, энергии). Вероятность каждого макросостояния пропорциональна числу микросостояний, которыми оно осуществляется.

Из молекулярно-кинетической теории следует, что давление газа создается за счет ударов его молекул в процессе теплового движения о стенки сосуда. Зная в какой-то момент времени координаты, направление движения и скорость каждой молекулы, можно было бы рассчитать давление газа в каком-то объеме. Но практически такой расчет неосуществим, так как обычно число молекул в системе огромно (один моль газа содержит 6,01 10²³ молекул). С другой стороны, зная величину объема и температуру, можно легко рассчитать давление газа по уравнению Менделеева-Клапейрона. Таким образом, состояние данного количества газа можно описать двумя макропараметрами (температурой и объемом) или очень большим количеством микросостояний, характеризующих кинетические особенности каждой молекулы в данный момент времени.

Для того чтобы понять, как число микросостояний системы связано с макропараметрами рассмотрим следующий пример. Пусть система состоит из 2 молекул идеального газа, которые находятся в объеме, состоящем из N маленьких объемов, каждый из которых соизмерим с размером молекулы (т.е. в каждом микрообъеме может быть одна молекула). На схеме эти объемы изображены в виде клеток. Допустим, наша система состоит из 5 клеток («микрообъемов»).

Размещения проведем следующим образом: одну молекулу помещаем в 1-ю клетку, а вторую - попеременно во 2-ю или в 3-ю, 4-ю или в 5-ю.

·	·							·	·
·		·						·		·
·			·
·				·
	·	·							·	·
	·		·
	·			·

Таким образом, число размещений двух молекул при условии, что одна молекула находится в 1-й клетке, будет 4. Затем одну молекулу помещаем во вторую клетку, а другую – в 3-ю, 4-ю или в 5-ю и т.д.

В общем случае число размещений (C^x_N) x молекул по N клеткам, при условии, что x N (для газов х N) равно:

CxN = .

(3)

Число микросостяний (или способов) которыми может быть реализовано данное макросостояние системы, называется термодинамической вероятностью (W).
W = C^x_N . (4)

Для больших x и N:

W  Nx .

(5)

Объем системы равен 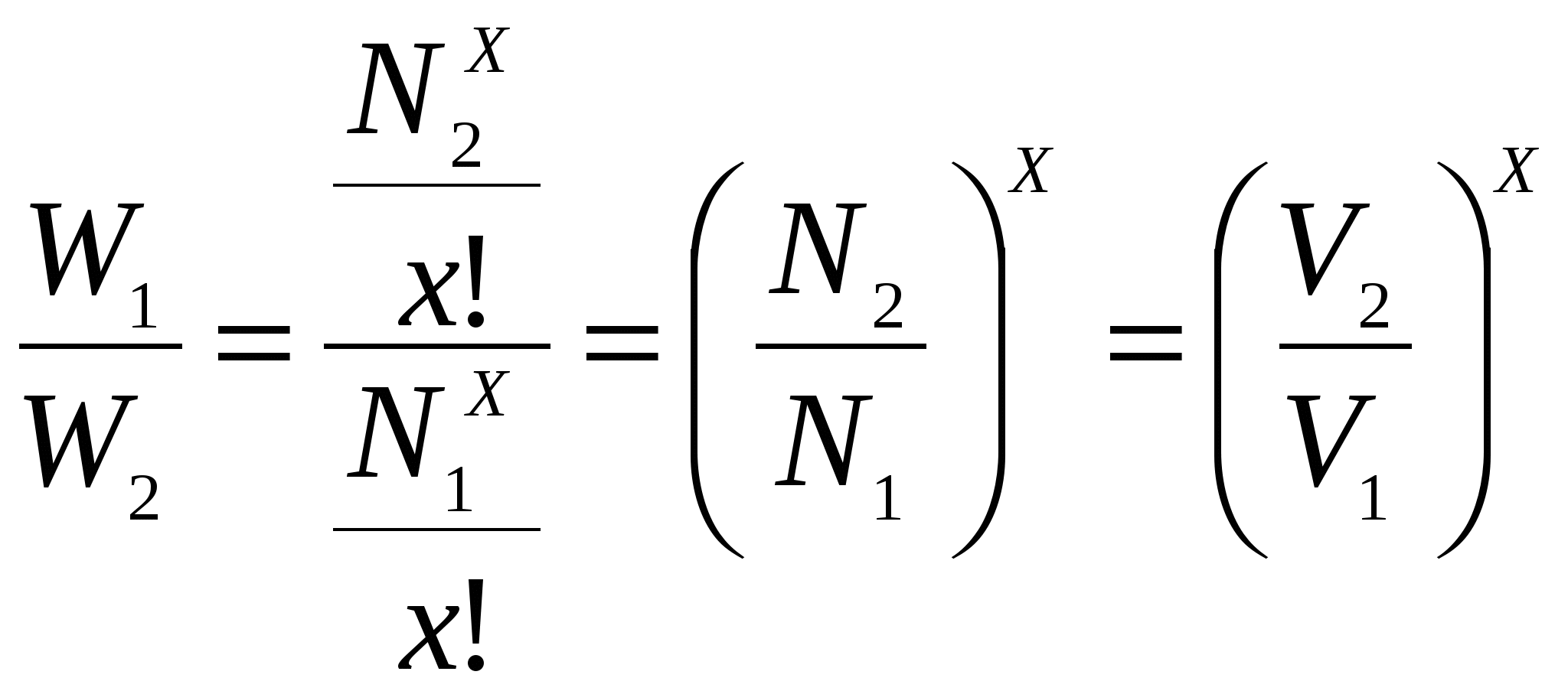, где - величина одного микрообъема. Отсюда . Тогда отношение количества микросостояний для двух систем с разным объемом, т.е. разным числом микрообъемов N, при одинаковом количестве молекул х будет:
(6)

Для 1 моля газа х = N_a= 6,02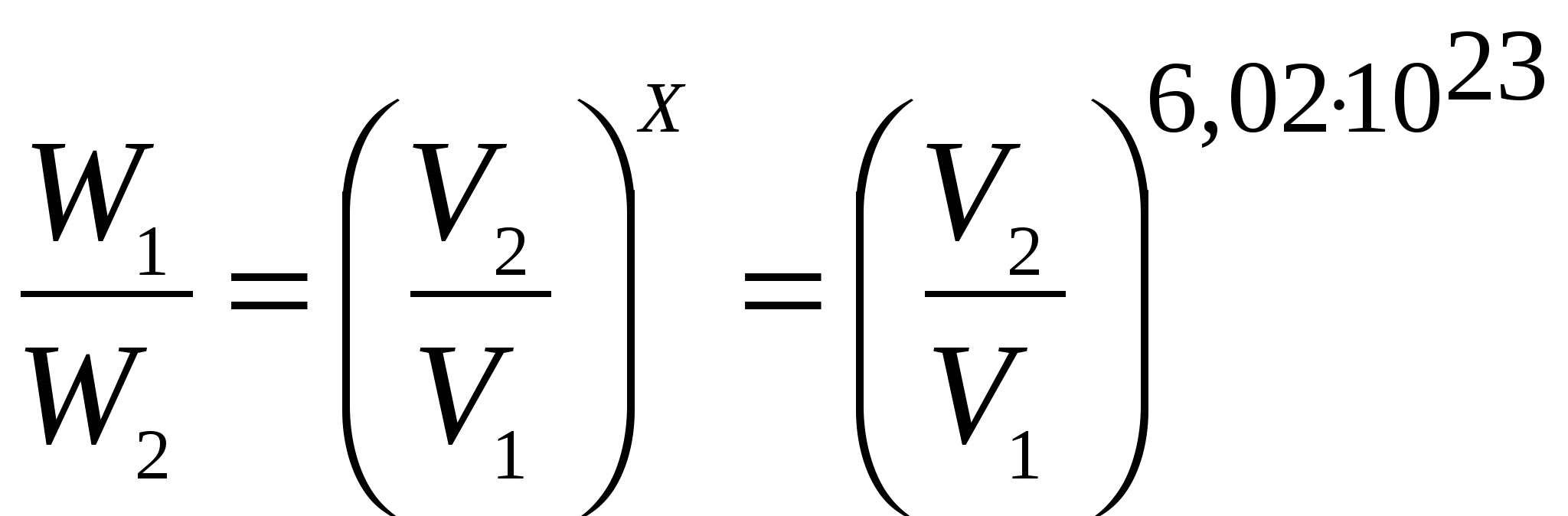10²³.

(7)
Из уравнений (6) и (7) видно, что термодинамические вероятности выражаются очень большими числами и практически пользоваться им неудобно. Поэтому более целесообразным оказалось характеризовать степень беспорядка системы величиной энтропии.

Таким образом, энтропия количественно характеризует термодинамическую вероятность того или иного состояния индивидуального вещества или системы.

Понятие энтропии ввел в науку Р. Клаузиус, теоретически исследуя работу тепловой машины. Приведенную теплоту , получаемую системой, Клаузиус отождествил с изменением функции состояния этой системы – энтропией S:
(8)
где С_р- мольная теплоемкость (р = const);

- бесконечно малое приращение теплоты.
Связь энтропии с термодинамической вероятностью установил Л. Больцман (1886г.), соответствующее уравнение (9) названо его именем:

S = klnW,

(9.)

где S - энтропия; размерность энтропии ;

W - термодинамическая вероятность;

k - константа Больцмана, k = , где

R - газовая постоянная (8,31);

N_А - число Авогадро (6,02·10²³ частиц в 1 моле).
Из этих уравнений видно, что чем больше термодинамическая вероятность системы, тем больше энтропия.

В изолированной системе самопроизвольно могут идти любые процессы - электрические, магнитные, тепловые и т.д. только при условии возрастания энтропии системы.

Это одна из формулировок второго закона термодинамики.

Из уравнения (6) следует, что чем больше термодинамическая вероятность системы, тем больше энтропия.

Термодинамическая вероятность связана со степенью беспорядка в расположении частиц системы. Например, из трех агрегатных состояний вещества (кристаллическое, жидкое, газообразное) наибольшей степенью беспорядка характеризуется газ, а наименьшей – кристалл.

При прочих равных условиях, вещество обладает минимальным значением энтропии в кристаллическом состоянии, а максимальным – в газообразном:

S_(кр.) < S_(ж.) < S_(г.) .
В отличие от энтальпии образования вещества, которая является относительной величиной, энтропия вещества может быть определена в абсолютных значениях для заданных условий.

Стандартная энтропия вещества представляет собой энтропию вещества (с указанием фазового состояния) при температуре 298 К и давлении 101,3 кПа. Стандартная энтропия вещества, например для NaCl_(тв.) обозначается: S^о_298,Na(тв).

Для растворенных веществ и ионов в растворе стандартное состояние отвечает молярной концентрации, равной 1 моль/л, но при этом предполагается, что раствор обладает свойствами бесконечно разбавленного раствора.

Стандартная энтропия любого вещества является положительной величиной (S^о₂₉₈ > 0), изменения энтропии в процессах (DS) могут быть как положительными, так и отрицательными.

Энтропия является функцией состояния, и для нее характерны все свойства функций состояния.

Изменение энтропии химической реакции равно разности суммы энтропий продуктов реакции и исходных веществ с учетом стехиометрических коэффициентов.

Так в стандартных условиях для реакции:
aA + bB = сС + dD
DS ^о_p =(cS^о_C+ dS^о_D) - (aS^о_А+ bS^о_В),
где DS^о_p- изменение энтропии для данной реакции, Дж/К;

S^о_А, S^о_В, S^о_C, S^о_D, - стандартные значения энтропий веществ, участвующих в реакции, Дж/моль·К.

Если реакция проводится в условиях, отличных от стандартных, то для расчета изменения энтропии реакции, энтропии веществ следует пересчитать применительно к данным условиям. Следует помнить, что на практике особенно сильное влияние на изменение энтропии химической реакции оказывает образование или поглощение газообразных веществ.