Основы химической термодинамики

Название	Основы химической термодинамики
Анкор	PC1E2010.rtf
Дата	02.02.2017
Размер	2.79 Mb.
Формат файла
Имя файла	PC1E2010.rtf
Тип	Документы #1881
страница	6 из 7

1 2 3 4 5 6 7

Основное уравнение термодинамики. Это уравнение объединяет формулы первого и второго начала термодинамики:

Q= dU+ р dV, (3.42)

. (3.43)
^Вместо Q в уравнение, выражающее второе начало термодинамики, подставим его выражение (3.42):

. (3.44)Это и есть основное уравнение термодинамики.

В заключение еще раз отметим, что если первый закон термодинамики содержит энергетический баланс процесса, то второй закон показывает его возможное направление.

В системе, не совершающей никакой работы, кроме работы расширения, и находящейся при постоянных температуре и давлении (Р = const, Т = const), самопроизвольно могут протекать только те процессы, которые приводят к уменьшению изобарно-изотермического потенциала системы (G). Когда G достигнет минимального значения при данных Р и Т, система приходит в равновесие и процесс прекращается.

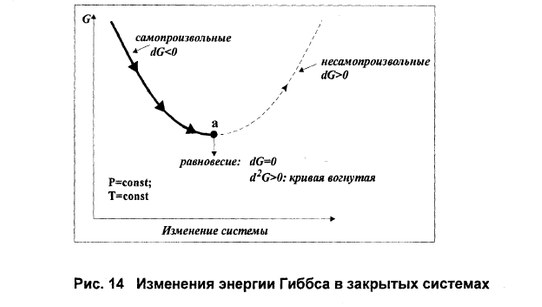
Обозначим величины так, как на рис. 1.15 (см. стр. 30), тогда $c:\documents and settings\admin\рабочий стол\физхим\b00001882-84.png$
если 1) A = PdV; 2) Р = const, Т = const, то при самопроизвольном процессе, протекающем неравновесным путем G₂ – G₁ < 0 dG < 0 G < 0		если 1) A = PdV; 2) Р = const, Т = const, то при равновесии G₂ – G₁ = 0 dG =0 G =0

Многие физические и химические процессы протекают при постоянном давлении и температуре, если они проводятся в открытых термостатированных реакторах. О направлении процессов и равновесии в таких системах судят по изменению изобарно-изотермического потенциала (свободной энергии) системы (G).

Если система не совершает никакой работы и ее объем и температура остаются постоянными (^ V = const, Т = const), то в такой системе самопроизвольно могут протекать только те процессы, которые приводят к уменьшению изохорно-изотермического потенциала системы (F). Когда F достигнет минимального при данных V и Тзначения, система приходит в равновесие, и процесс прекращается.

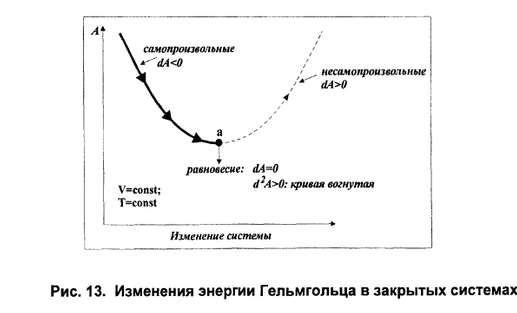
$c:\documents and settings\admin\рабочий стол\физхим\b00001882-82.png$ Итак,
если 1) A = dVP + … = 0; 2) V = const, Т = const, то при самопроизвольном процессе F₂ – F₁ < 0 dF < 0 F < 0		если 1) A = dVP + … = 0; 2) V = const, Т = const, то при равновесии F₂ – F₁ = 0 dF =0 F =0

Процессы протекают при постоянном объеме и температуре, если их проводят в закрытых, термостатированных аппаратах, например, в автоклавах. Критерием протекания процесса в этом случае служит изменение изохорно-изотермического потенциала (энергии Гельмгольца) системы. Опираясь на второй закон термодинамики легко доказать следующее правило.

$c:\documents and settings\admin\рабочий стол\физхим\b00001882-109.png$

Энергия Гиббса, энергия Гельмгольца. Применение этих термодинамических функций для определения состояния равновесия и направления химического процесса.(ответ в 27)
Энергия Гиббса и энергия Гельмгольца. Применение этих характеристических термодинамических функций для определения состояния равновесия и направления самопроизвольных процессов в изотермических условиях.(ответ в 27)

Если процесс протекает самопроизвольно, то внутренняя энергия (энтальпия) должны уменьшаться, а энтропия увеличиваться. Для сравнения этих величин их надо выразить в одних единицах, а для этогоΔS умножить на T. В этом случае имеем ΔН – энтальпийный фактор и ТΔS- энтропийный фактор.

В ходе реакции частицы стремятся к объединению, что ведет к уменьшению энтальпии (ΔН < 0), с другой стороны – должна возрастать энтропия, т.е. увеличиваться число частиц в системе (ТΔS > 0). "Движущая сила" реакции определяется разностью между этими величинами и обозначается ΔG.

ΔG_p_,_T = ΔH – TΔS

и называется изменением энергии Гиббса (изобарно-изотермический потенциал).

Энергия Гиббса - это часть энергетического эффекта реакции, которую можно превратить в работу, поэтому ее называют свободной энергией. Это тоже термодинамическая функция состояния и, следовательно, для реакции

bB + dD =lL + mM,

энергию Гиббса химической реакции можно рассчитать как сумму энергий Гиббса образования продуктов реакции за вычетом энергий Гиббса образования исходных веществ с учетом стехиометрических коэффициентов по формуле:

ΔG = lΔ_fG_L + mΔ_fG_M – dΔ_fG_D – bΔ_fG_B.

где Δ_fG –энергия Гиббса образования веществ.

Энергия Гиббса образования веществ это изменение энергии Гиббса системы при образовании 1 моль вещества из простых веществ, устойчивых при 298 К.

Энергия Гиббса образования простых веществ Δ_fG принимается равной нулю. Если образующееся вещество и исходные простые вещества находятся в стандартных состояниях, то энергия Гиббса образования называется стандартной энергией Гиббса образования вещества Δ_fG⁰. Ее значения приводятся в справочниках.

Полученное значение ΔG является критерием самопроизвольного течения реакции в прямом направлении, если ΔG< 0. Химическая реакция не может протекать самопроизвольно в прямом направлении, если энергия Гиббса системы возрастает, т.е. ΔG > 0. Если ΔG = 0, то реакция может протекать как в прямом, так и в обратном направлениях, т.е. реакция обратима.

Направление химических реакций зависит от их характера. Так, условие ΔG < 0 соблюдается при любой температуре для экзотермических реакций (ΔН < 0), у которых в ходе реакции возрастает число молей газообразных веществ, и, следовательно, энтропия (ΔS > 0). У таких реакций обе движущие силы (ΔН) и (ТΔS) направлены в сторону протекания прямой реакции и ΔG < 0 при любых температурах. Такие реакции являются необратимыми.

Наоборот, эндотермическая реакция (ΔН > 0), в результате которой уменьшается число молей газообразных веществ (ΔS< 0) не могут протекать самопроизвольно в прямом направлении при любой температуре, т.к. всегда ΔG > 0.

Если в результате экзотермической реакции (ΔН < 0) уменьшается число молей газообразных веществ и, соответственно, энтропия (ΔS < 0), то при невысокой температуре ΔН > TΔS и реакция возможна в прямом направлении (ΔG < 0). При высоких температурах ΔH < TΔS и прямая реакция самопроизвольно протекать не может (ΔG > 0), а обратная реакция возможна.

Для определения температуры равновесия можно воспользоваться условием:

Т_р = ΔН/ΔS,

где Т_р – температура, при которой устанавливается равновесие, т.е. возможность протекания прямой и обратной реакций.

Если в результате эндотермической реакции (ΔН > 0) увеличивается число молей газообразных веществ и энтропия системы (ΔS > 0), то при невысоких температурах, когда ΔН > ТΔS, самопроизвольно прямая реакция идти не может (ΔG> 0), а при высоких температурах, когда ΔН < TΔS , прямая реакция может протекать самопроизвольно (ΔG < 0).

Связь между ΔG и ΔG⁰ выражается уравнением изотермы Вант-Гоффа, которая для реакции

bB + dD = lL + mM

записывается в виде:

либо в виде:

где - относительные парциальные давления соответствующих веществ; концентрации соответствующих растворенных веществ.

Итак, энергия Гиббса позволяет определить возможность протекания реакции расчетным путем, не прибегая к дорогостоящим и длительным экспериментам.

В изохорно-изотермических условиях свободная энергия называется энергией Гельмгольца или изохорно-изотермическим потенциалом и равна

Она характеризует направление и предел самопроизвольного течения химической реакции при изохорно-изотермических условиях, которое возможно при ΔF < 0

Применение таблиц стандартных термодинамических величин для расчета ΔS ΔG ΔA и химических реакций.
Зависимость энергии Гиббса и энергии Гельмгольца химической реакции от температуры. Уравнения Гиббса-Гельмгольца. Связь и химической реакции.

Зависимость энергии Гиббса от температуры и давления
H – TS U + pV– TS G (7.21)

G_pTS,  H -T _rG_pT _rH -T_rS(7.22)

H характеризует общее изменение энергии системы в ходе процесса, а изменение энергии Гиббса показывает, какая часть ее может быть превращена в полезную работу, поэтому раньше ее называли свободной энергией, в противоположность энтропийному члену, который характеризовал связанную энергию, недоступную для превращения в работу.

а)

; б)

(7.20)

Из уравнения 7.20а следует, что с ростом давления энергия Гиббса увеличивается, так как V> 0, но темп роста замедляется, так как объем постепенно уменьшается. Причем для разных идеальных газов эти кривые будут одинаковыми.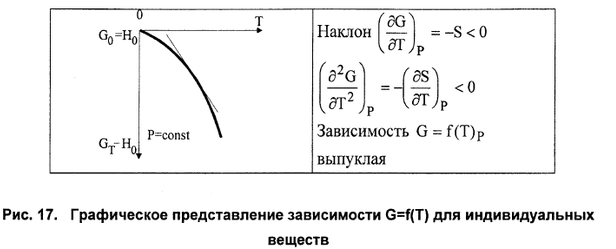

$c:\documents and settings\admin\рабочий стол\физхим\b00001882-89.png$ $c:\documents and settings\admin\рабочий стол\физхим\b00001882-89 (1).png$

Рис. 7.1. Зависимость энергии Гиббса от давления и температуры.

С ростом температуры энергия Гиббса убывает, так как энтропия всегда положительна, причем падение энергии Гиббса будет ускоряться из-за роста энтропии при повышении температуры.

$c:\documents and settings\admin\мои документы\downloads\b00001882-86.png$ $c:\documents and settings\admin\мои документы\downloads\b00001882-87.png$ $c:\documents and settings\admin\мои документы\downloads\b00001882-88.png$

ГИББСА - ГЕЛЬМГОЛЬЦА УРАВНЕНИЯ - термо-динамич. соотношения, устанавливающие связь между внутренней энергией и Гелъмголъца энергией (свободной энергией) F или между энтальпией H и Гиббса энергией (свободной энтальпией) G:

где T - темп-pa, V - объём, P - давление. Установлены в 1875 Дж. У. Гиббсом, ур-ние (1) использовал Г. Гельмгольц (H. Helmholtz). Ур-ние (1) следует из определения энергии Гельмгольца F=U-TS и выражения для энтропии

, ур- ние (2)-из определения энергии Гиббса G=H-TS и выражения для энтропии

Ур-ние (1) позволяет по энергии Гельмгольца F(T, V)найти внутр. энергию U(T, V)и, следовательно, теплоёмкость при пост. объёме. Ур-ние (2) позволяет по энергии Гиббса G(T, P)найти энтальпию H(T, P)и, следовательно, теплоёмкость при пост. давлении.

Макс. работа, к-рую может совершить система в тепловом контакте с окружающей средой

, удовлетворяет Г. - Г. у.

.

Эта макс. работа за вычетом работы против сил давления P(V₂- V₁)(максимальная полезная работа)

удовлетворяет Г. - Г. у.

. (Различие между макс. работой и максимальной полезной работой существенно для газообразных систем.) Г. - Г. у. применяются в термодинамич. теории гальванич. элеменюв, использовались при установлении третьего начала термодинамики и его следствий

Системы переменного состава. Химический потенциал компонента системы. Зависимость химического потенциала от давления и температуры. Условия равновесия и самопроизвольного протекания химического процесса в системах переменного состава.

Раствором называется гомогенная, молекулярно-дисперсная система, состав которой можно изменять непрерывно в некотором конечном или бесконечном интервале.

По агрегатному состоянию растворы разделяются на твердые, жидкие и газообразные. Если растворитель и растворенное вещество имеют разные агрегатные состояния, то растворителем рассматривают обычно то вещество, агрегатное состояние которого совпадает с агрегатным состоянием раствора. Если же компоненты раствора и раствор имеют одинаковое агрегатное состояние, то за растворитель считают то вещество, которого больше, хотя для термодинамики это безразлично.

Состав раствора измеряется его концентрацией. Существуют следующие основные определения концентрации:

мольная доля (х) – число молей вещества в 1 моле раствора;

моляльность (m) – число молей растворенного вещества в 1000 г растворителя;

молярность (с) – число молей растворенного вещества в 1 л раствора;

массовое содержание (р) – число грамм растворенного вещества в 100 г раствора.

Характеристические функции многокомпонентных систем.

Первый и второй законы термодинамики, из которых следуют фундаментальные уравнения, были получены для закрытых систем, т.е. систем, процессы в которых не приводят к изменению количества компонентов. Реально же чаще встречаются системы, в которых при различных процессах изменяются количества компонентов. Это может происходить, скажем, при фазовых превращениях или вследствие протекания химической реакции. При этом может изменяться состав, как отдельных частей, так и системы в целом.

Поэтому внутренняя энергия (и другие функции состояния) открытых систем будут изменяться не только за счет сообщения системе теплоты и произведенной системой работы, но и за счет изменения состава системы. Следовательно для открытых систем характеристические функции будут функциями не только их двух естественных переменных, но и функциями числа молей всех веществ , составляющих систему:

U = U ( S, v, n1……………….nk ),

H = H ( S, p, n1 ………….. nk ),

F = F ( T, v, n1…………… nk ),

G = G ( T, p, n1……………nk ).

Хими́ческий потенциа́л  — термодинамическая функция, применяемая при описании состояния систем с переменным числом частиц. Определяет изменение термодинамических потенциалов (энергии Гиббса, внутренней энергии, энтальпии и т. д.) при изменении числа частиц в системе. Представляет собой энергиюдобавления одной частицы в систему без совершения работы. Определение химического потенциала можно записать в виде:

$</h2> de = tds - pdv + \mu dn$ где Е — энергия системы, S — её энтропия, N — количество частиц в системе.

Эта формула определяет, кроме химического потенциала , также давление P и температуру T.

Для систем, состоящих из одного компонента, можно доказать, что химический потенциал задаётся формулой

$\mu = {e - ts + pv \over n}={g \over n}$ ,где  -потенциал Гиббса

Если энергия системы зависит не от объёма, а от других термодинамических параметров , исходная формула принимает вид $</h2> de = tds - \sum_i a_i da_i + \mu dn$

Если в системе имеется несколько разных типов частиц, есть столько же разных химических потенциалов. Связь химического потенциала со свободной энергией называется Большим термодинамическим потенциалом.

Условия равновесия в многокомпонентных гетерогенных системах.

Пусть р, Т =Const, тогда      . Если в системе имеются фазы (') и (''), то при переходе dn_i молей i–ого компонента из фазы (') в фазу ('') изменение энергии Гиббса системы dGбудет складываться из изменении энергий Гиббса обеих фаз dG'иdG'': .

Если система закрытая, то    , а если она к тому же и равновесна, то dG= 0 и, следовательно, , т.е. химические потенциалы данного компонента во всех фазах системы, находящейся в равновесии, равны между собой.

Самопроизвольный неравновесный процесс может идти только в сторону уменьшения энергии Гиббса системы dG< 0 (p,T=const).

Предположим, что , т.е. фаза (') теряет i–ый компонент, но , значит .

Если же , тогда . Таким образом, компонент самопроизвольно переходит из фазы, в которой его химический потенциал больше, в фазу, в которой его химический потенциал меньше.

Эти условия равновесия и самопроизвольности процессов переноса вещества в многокомпонентных системах являются обобщением таковых для однокомпонентных систем (см. гл. 6). Кроме того, легко заметить, что химический потенциал чистого вещества равен его мольной энергии Гиббса.
ХИМИЧЕСКОЕ РАВНОВЕСИЕ

Краткая характеристика химического равновесия. Закон действующих масс, термодинамическое обоснование (все реагенты – идеальные газы). Термодинамическая и эмпирическая константы равновесия.

Химическое равновесие — состояние химической системы, в котором обратимо протекает одна или несколько химических реакций, причём скорости в каждой паре прямая-обратная реакция равны между собой. Для системы, находящейся в химическом равновесии, концентрации реагентов, температура и другие параметры системы не изменяются со временем

А₂ + В₂ ⇄ 2AB

В химической термодинамике закон действующих масс связывает между собой равновесные активности исходных веществ и продуктов реакции, согласно соотношению:

$k_a = \prod_{i=1}^n a_i^{{\nu}_i}$ где

— активность веществ. Вместо активности могут быть использованы концентрация (для реакции в идеальном растворе), парциальные давления (реакция в смеси идеальных газов), фугитивность (реакция в смеси реальных газов);

— стехиометрический коэффициент (для исходных веществ принимается отрицательным, для продуктов — положительным);

— константа химического равновесия. Индекс «a» здесь означает использование величины активности в формуле.

На практике в расчётах, не требующих особой точности, значения активности обычно заменяются на соответствующие значения концентраций (для реакций в растворах) либо парциальных давлений (для реакций между газами). Константу равновесия при этом обозначают или соответственно. Впервые закон действующих масс был выведен из кинетических представлений Гульдбергом и Вааге, а термодинамический вывод его дан Вант-Гоффом в 1885 году^[3].

Пример: для стандартной реакции $\mathrm{a\,a + b\,b \ \rightleftharpoons \ c\,c + d\,d}$

константа химического равновесия определяется по формуле $k_c = {c^\mathrm{c}(\mathrm{c}) \cdot c^\mathrm{d}(\mathrm{d}) \over c^\mathrm{a}(\mathrm{a}) \cdot c^\mathrm{b}(\mathrm{b})}$

При наступлении химического равновесия в системе, когда скорость прямой реакции равна скорости обратной реакции и закон действующих масс формулируется следующим образом: отношение произведения равновесных концентраций (или парциальных давлений) продуктов реакции, взятых в степенях их стехиометрических коэффициентов, к произведению для исходных веществ есть величина постоянная.Этот параметр называемая константой равновесия К_равн.
Для обратимой гомогенной реакции:
ν_AA + ν _BB ó ν _DD + ν _F F
константа равновесия может быть выражена в виде отношения равновесных молярных концентраций реагирующих веществ - ^ K_C, равновесных парциальных давлений – K_P, равновесных молярных долей -K_X:

;

(1)

Между константами равновесия K_C, K_P и K_Xдля реакции с участием идеальных газов легко установить взаимосвязь, используя уравнение Менделеева – Клапейрона (pV=nRT) и закон Дальтона (p_i = X_i p₀ , где p_i – парциальное давление i-ого газа, p₀ – общее давление в системе, X_i – молярная доля i-ого газа):
K_P = K_C(RT)^Δν и K_P = K_X(p₀)^Δν (2),
где Δν = (ν_D+ν_F) – (ν_A + ν _B)
Константы K_P , K_Cи K_Xназываются эмпирическими константами равновесия, они могут быть численно равны, если Δν = 0, и иметь размерность, если Δν ≠ 0.
Термодинамическая константа равновесия K⁰ безразмерна и может быть вычислена из стандартной энергии Гиббса:

_r G⁰_T = - RT ln K⁰

Направление протекания химического процесса при заданных начальных условиях. Вывод и анализ уравнения изотермы химической реакции.

1 2 3 4 5 6 7