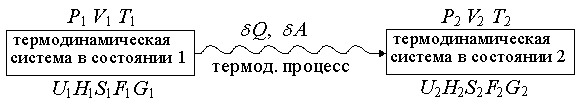Основное уравнение термодинамики. Это уравнение объединяет формулы первого и второго начала термодинамики:
Q = dU + р dV, (3.42)
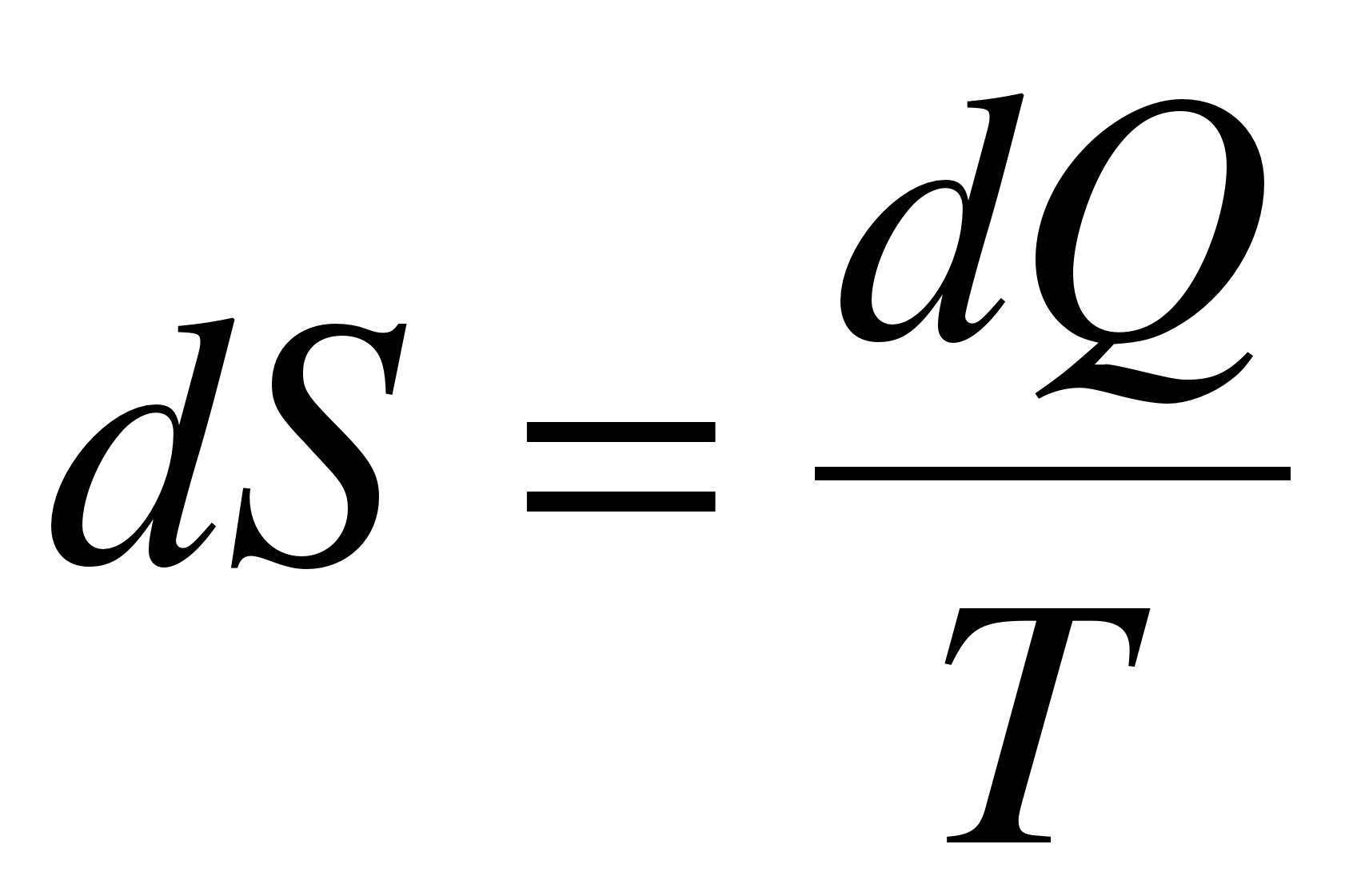 . (3.43) . (3.43)
^Вместо Q в уравнение, выражающее второе начало термодинамики, подставим его выражение (3.42):
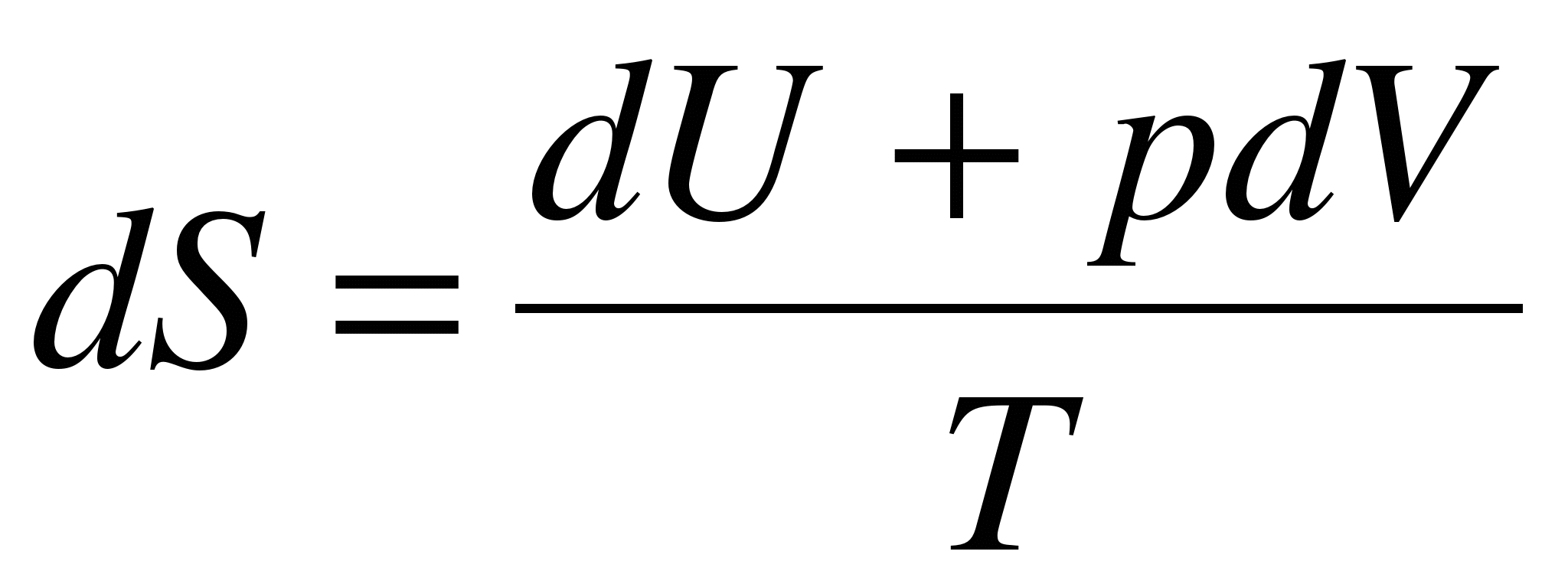 . (3.44)Это и есть основное уравнение термодинамики. . (3.44)Это и есть основное уравнение термодинамики.
В заключение еще раз отметим, что если первый закон термодинамики содержит энергетический баланс процесса, то второй закон показывает его возможное направление.
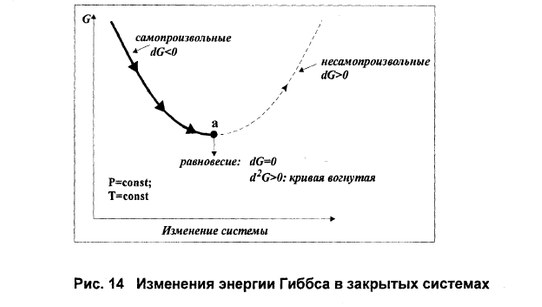
В системе, не совершающей никакой работы, кроме работы расширения, и находящейся при постоянных температуре и давлении (Р = const, Т = const), самопроизвольно могут протекать только те процессы, которые приводят к уменьшению изобарно-изотермического потенциала системы (G). Когда G достигнет минимального значения при данных Р и Т, система приходит в равновесие и процесс прекращается.
|
Обозначим величины так, как на рис. 1.15 (см. стр. 30), тогда
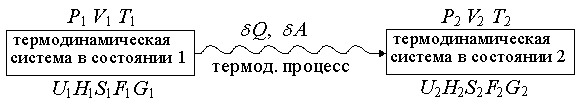 
|
если 1) A = PdV;
2) Р = const, Т = const,
то при самопроизвольном процессе, протекающем неравновесным путем
G2 – G1 < 0
dG < 0 G < 0
|
|
если 1) A = PdV;
2) Р = const, Т = const,
то при равновесии
G2 – G1 = 0
dG =0 G =0
|
|
Многие физические и химические процессы протекают при постоянном давлении и температуре, если они проводятся в открытых термостатированных реакторах. О направлении процессов и равновесии в таких системах судят по изменению изобарно-изотермического потенциала (свободной энергии) системы (G).
|
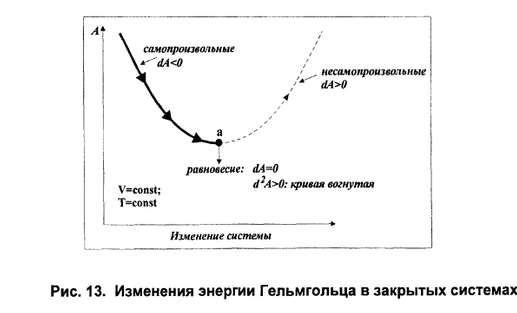
Если система не совершает никакой работы и ее объем и температура остаются постоянными (^ V = const, Т = const), то в такой системе самопроизвольно могут протекать только те процессы, которые приводят к уменьшению изохорно-изотермического потенциала системы (F). Когда F достигнет минимального при данных V и Тзначения, система приходит в равновесие, и процесс прекращается.
Итак,
|
если 1) A = dVP + … = 0;
2) V = const, Т = const,
то при самопроизвольном процессе
F2 – F1 < 0
dF < 0 F < 0
|
|
если 1) A = dVP + … = 0;
2) V = const, Т = const,
то при равновесии
F2 – F1 = 0
dF =0 F =0
|
|
Процессы протекают при постоянном объеме и температуре, если их проводят в закрытых, термостатированных аппаратах, например, в автоклавах. Критерием протекания процесса в этом случае служит изменение изохорно-изотермического потенциала (энергии Гельмгольца) системы. Опираясь на второй закон термодинамики легко доказать следующее правило.
|
Постулат Планка. Аналитический и графический методы определения абсолютной стандартной энтропии вещества.
|
Формулировка
постулата Планка
Энтропия индивидуального кристаллического вещества с идеально построенной кристаллической решеткой при Т = 0
К равна нулю. 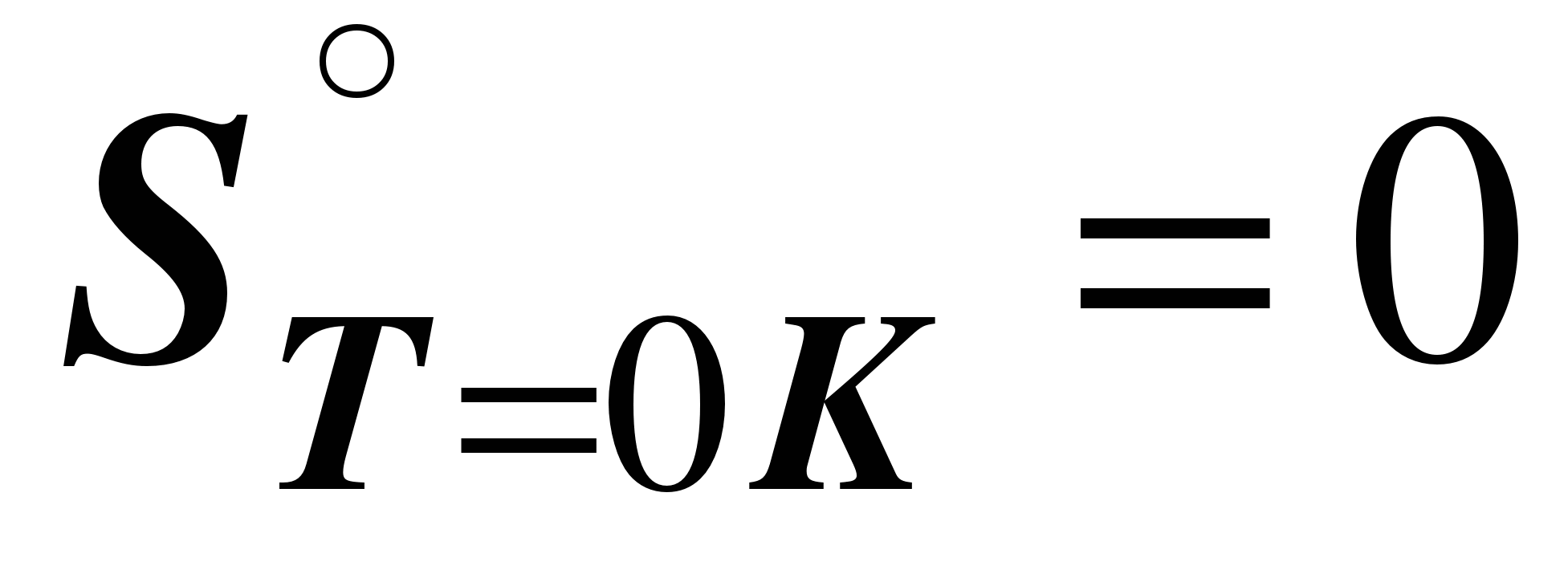 для идеального кристаллического вещества для идеального кристаллического вещества
Замечание
^ Энтропия стеклообразного (некристаллического) вещества и твердых растворов не равна 0 и при Т = 0 К.
Постулат Планка не вытекает из 1-го и 2-го законов термодинамики и не может быть доказан в рамках классической термодинамики
С помощью постулата Планка можно вычислить абсолютную величину энтропиииндивидуального вещества при любой температуре. Эта величина называетсяабсолютной энтропией вещества и обозначается ST°. Абсолютные энтропии большинства веществ рассчитаны и приведены в справочной литературе [4].
Для вычисления абсолютной энтропии газообразного вещества при температуре Tнеобходимо знать:
теплоемкость этого вещества в кристаллическом состоянии от температуры плавления (TПЛ.) и до температур, близких к абсолютному нулю;
Измерение теплоемкостей веществ в области низких температур является сложной задачей. В настоящее время методами низкотемпературной калориметрии исследованы многие вещества и получены их низкотемпературные теплоемкости.
теплоты фазовых переходов вещества (плавления, испарения и др.) при стандартном давлении;
температурные зависимости теплоемкости вещества в жидком состоянии в интервале от TПЛ. до TКИП. и газообразного вещества при температурах вышеTКИП..
Рассмотрим процесс нагревания какого либо индивидуального вещества от 0,К до температуры Т. Тогда изменение энтропии тела в результате его нагревания составит:
ΔS = S2 – S1 = ST - S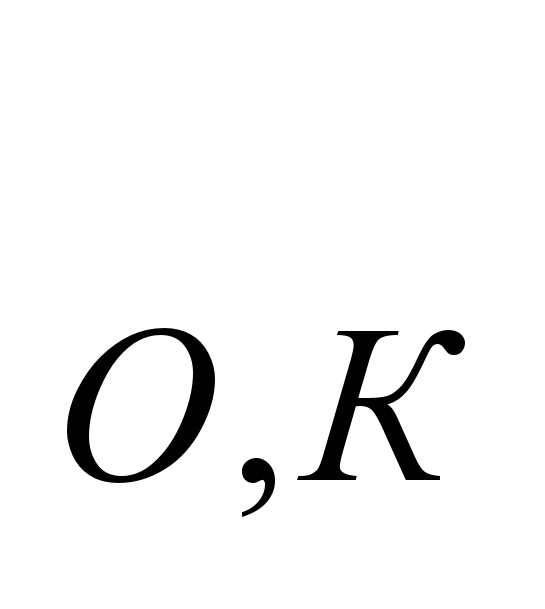 (5.19) (5.19)
Из третьего закона термодинамики следует, что S0,К = 0, тогда абсолютная энтропия тела при температуре Т будет представлять собой изменение энтропии тела в процессе его нагревания от 0,К до температуры Т:
ST = ΔS (5.20)
Пусть в процессе нагревания до температуры Т тело претерпевает превращения, каждое из которых сопровождается соответствующим изменением энтропии.
1.Нагревание твёрдого тела от абсолютного нуля до температуры плавления. Изменение энтропии тела в результате нагревания составит:
ΔS1 = 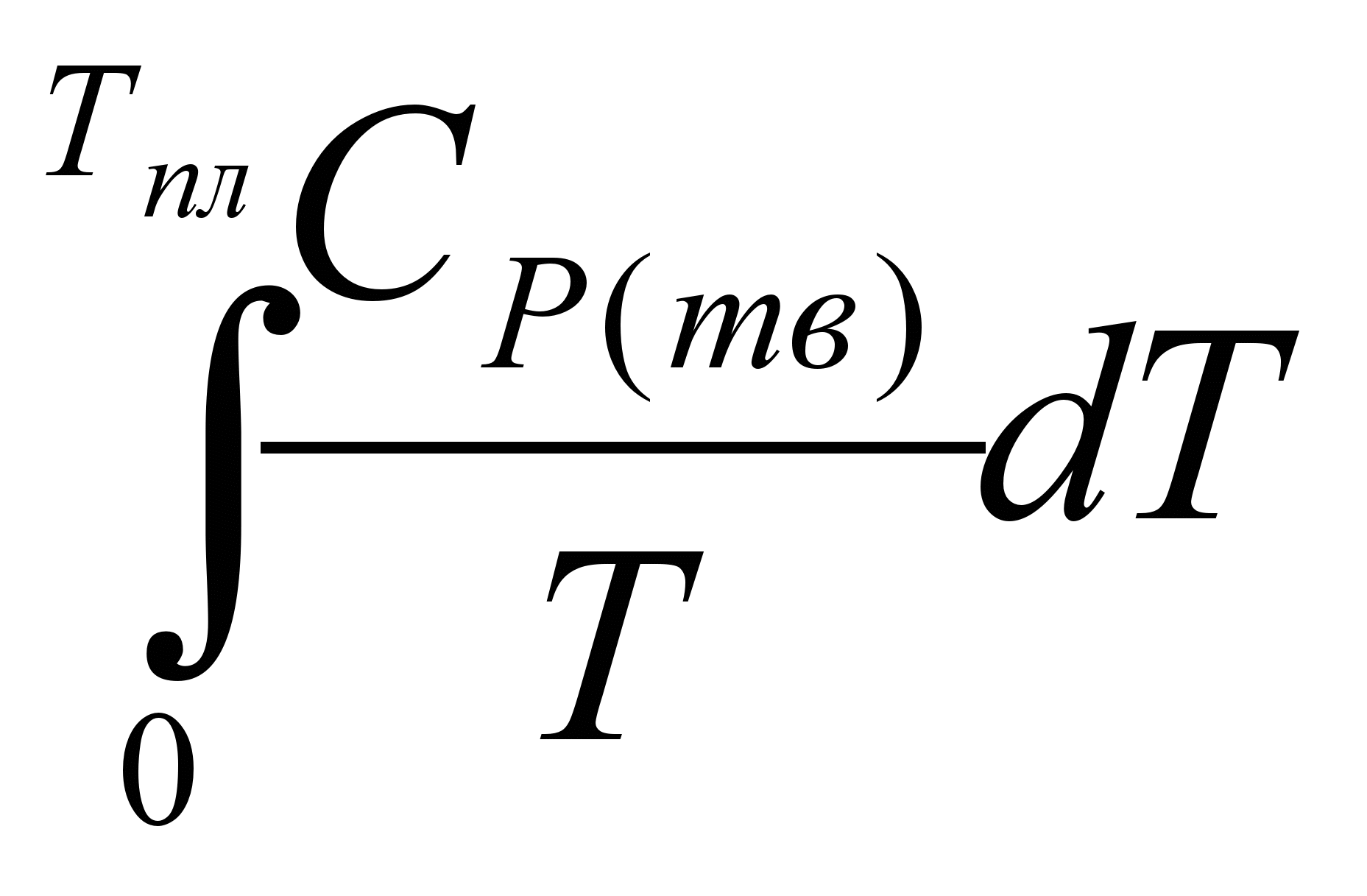 = = 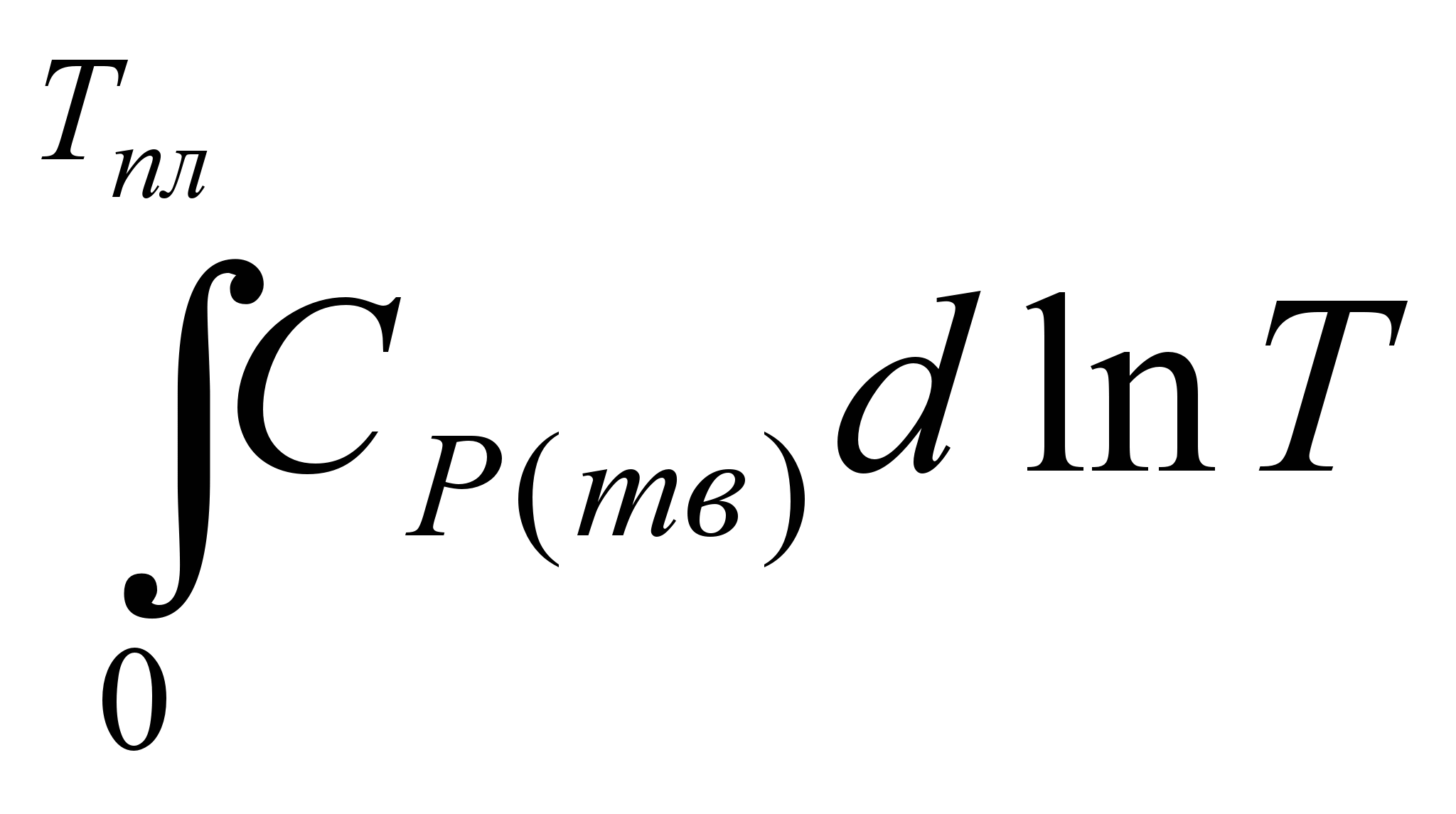 (5.21) (5.21)
2.Плавление твёрдого тела при температуре плавления. Процесс плавления твёрдого тела происходит при P = Const и Т = Const. Изменение энтропии при таких превращениях определяется из уравнения:
ΔS2 = 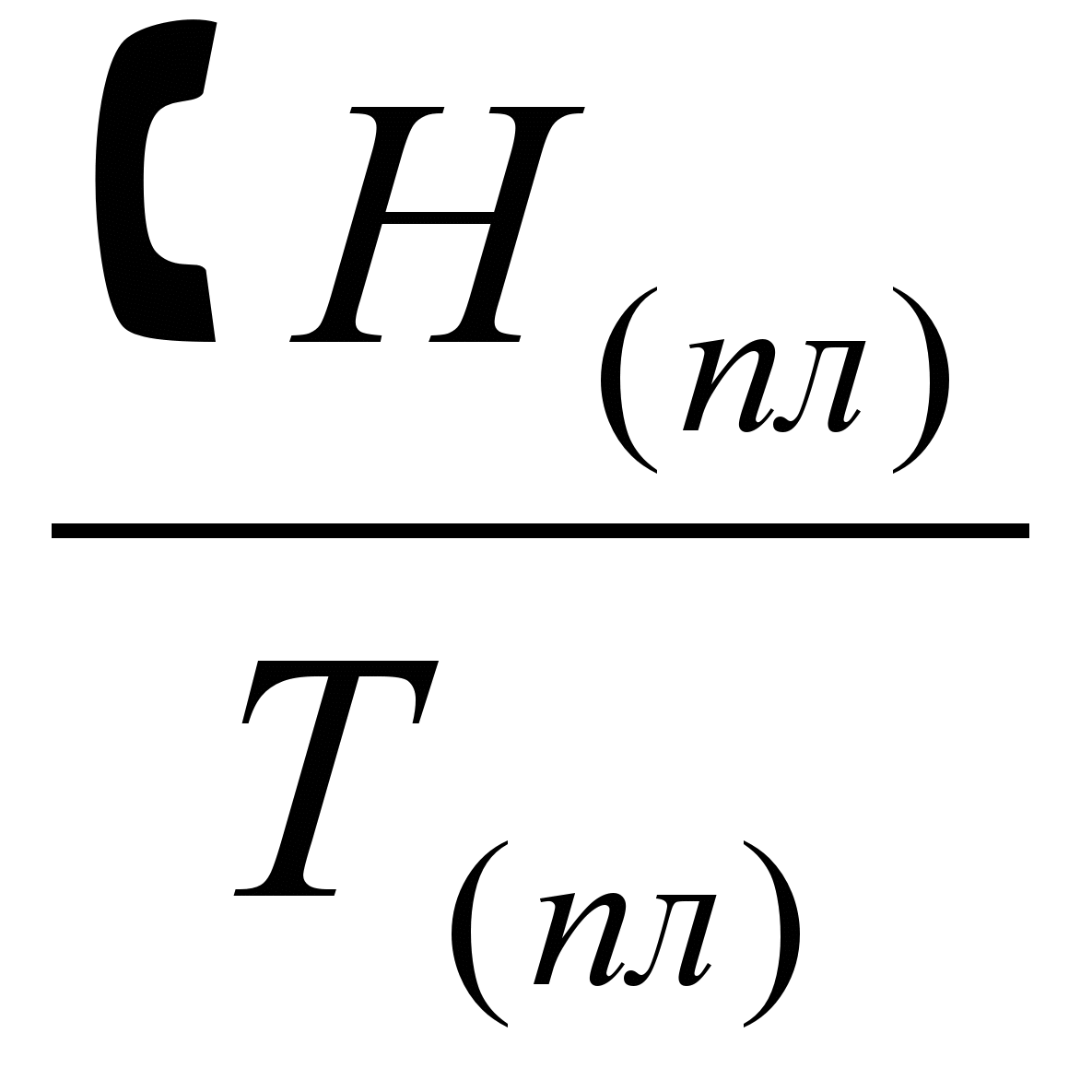 (5.22) (5.22)
3.Нагревание жидкого тела от температуры плавления до температуры
кипения. Изменение энтропии в этом случае составит:
ΔS3 = 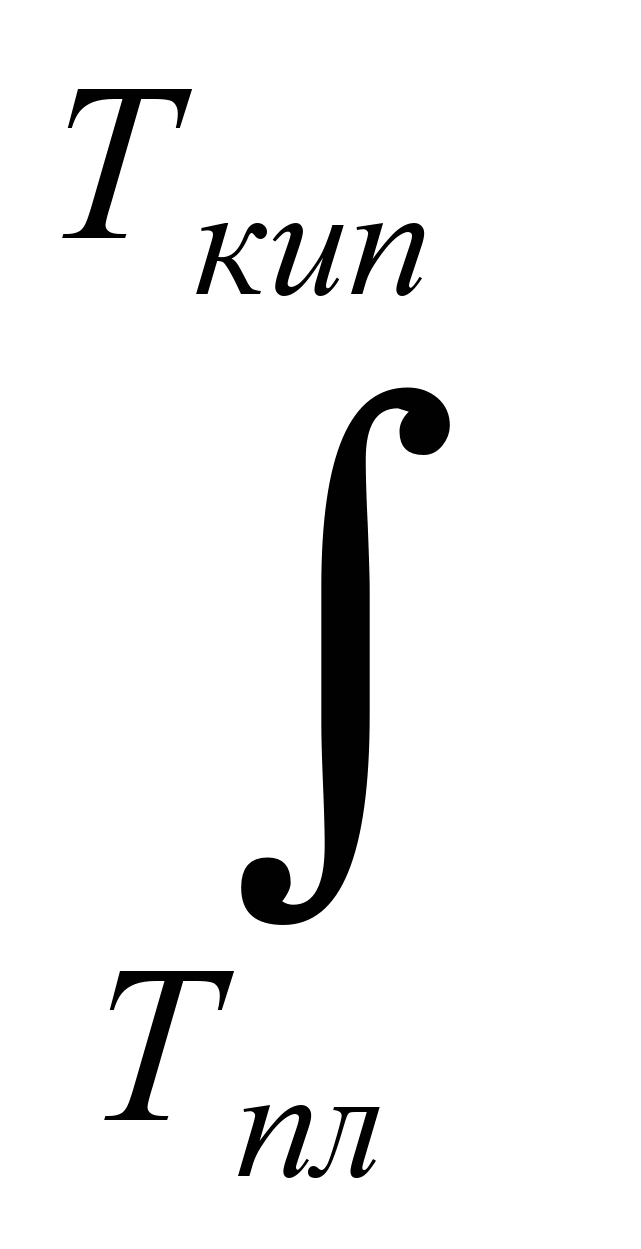 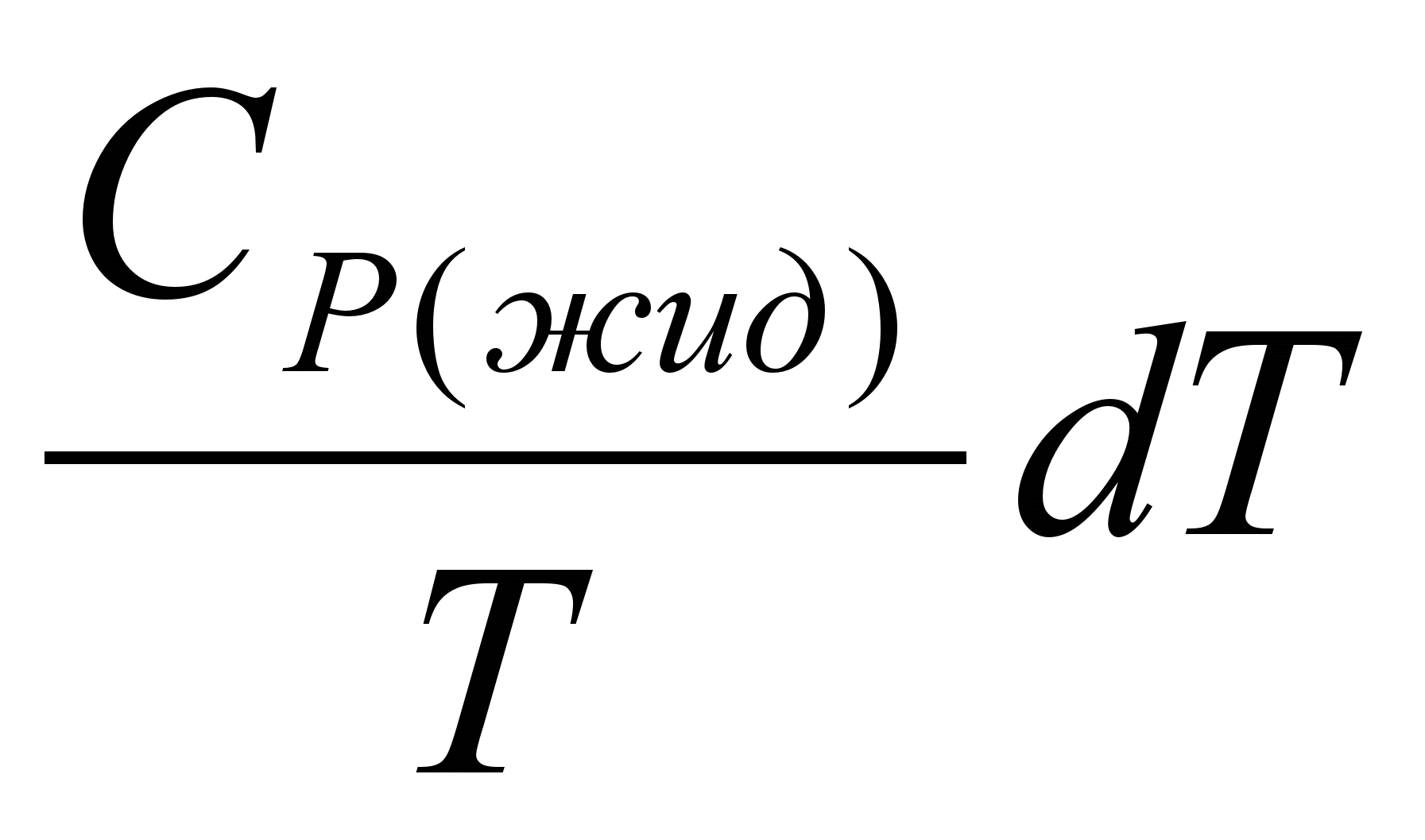 = =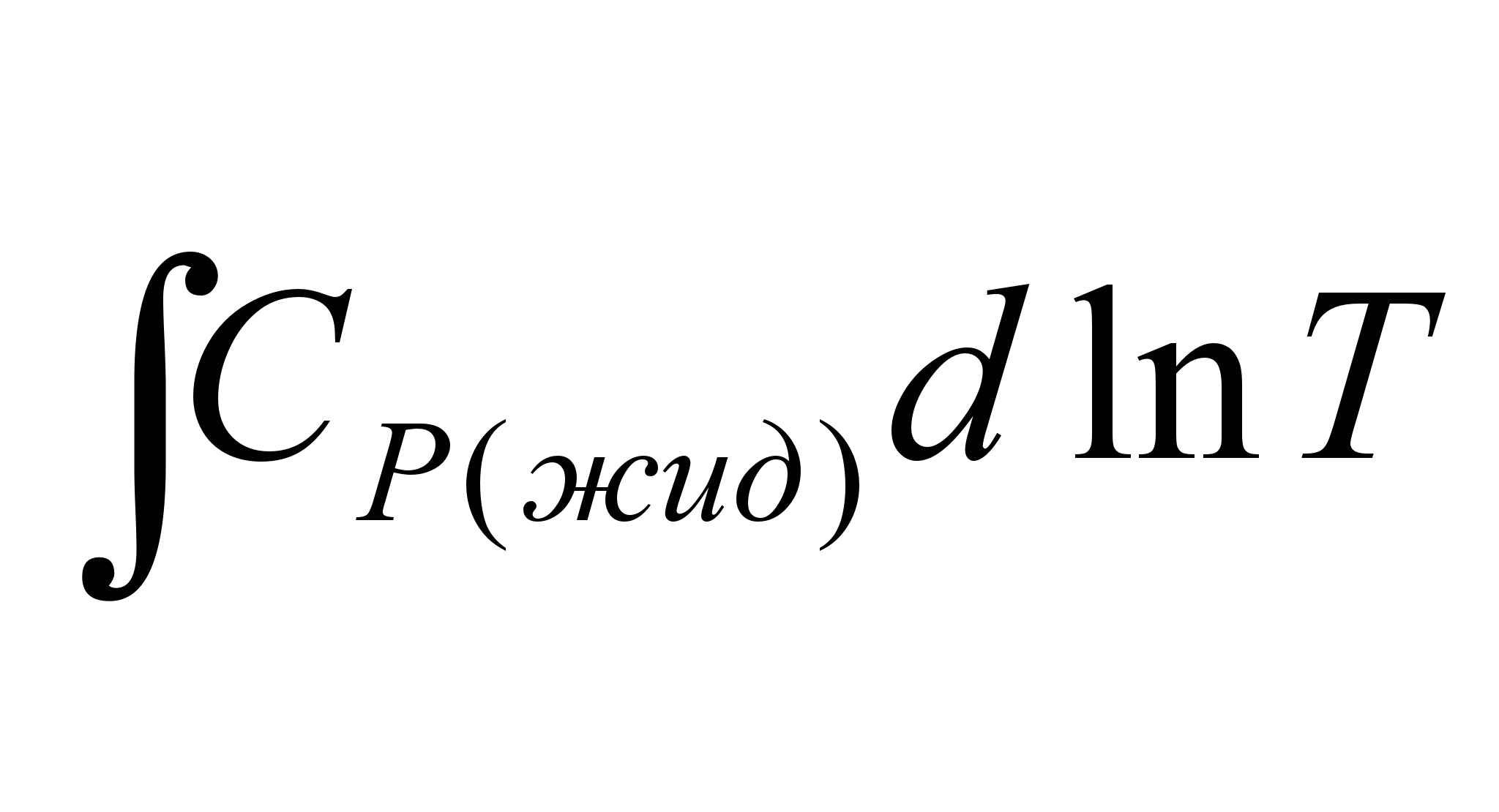 (5.23) (5.23)
4.Испарение тела при температуре кипения. Испарение при температуре
кипения происходит при P = Const и T = Const. Изменение энтропии в
процессе испарения составит:
ΔS4 = 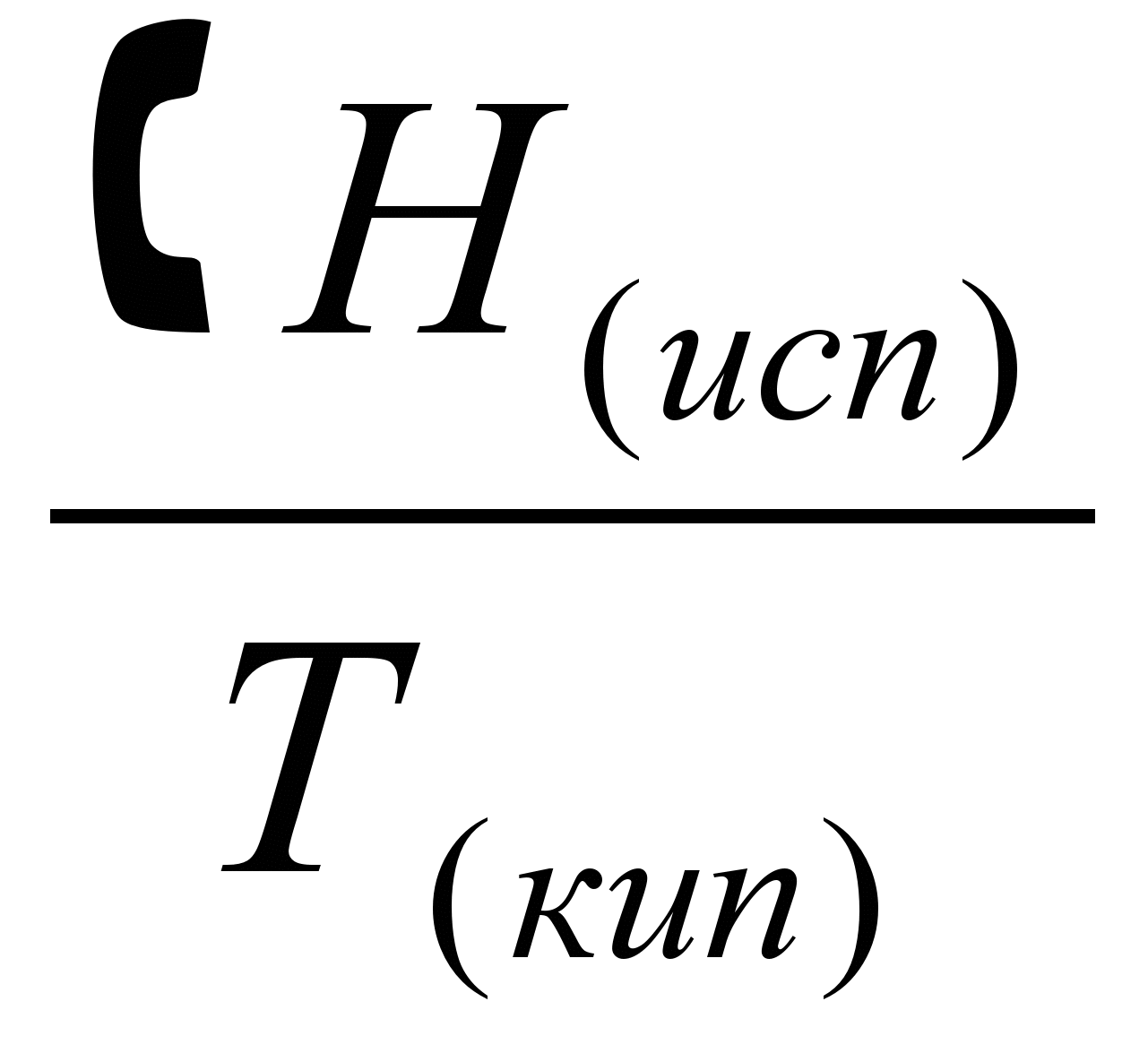 (5.24) (5.24)
5.Нагревание газообразного тела от температуры кипения до конечной температуры Т. Изменение энтропии в этом процессе составит:
ΔS5 = 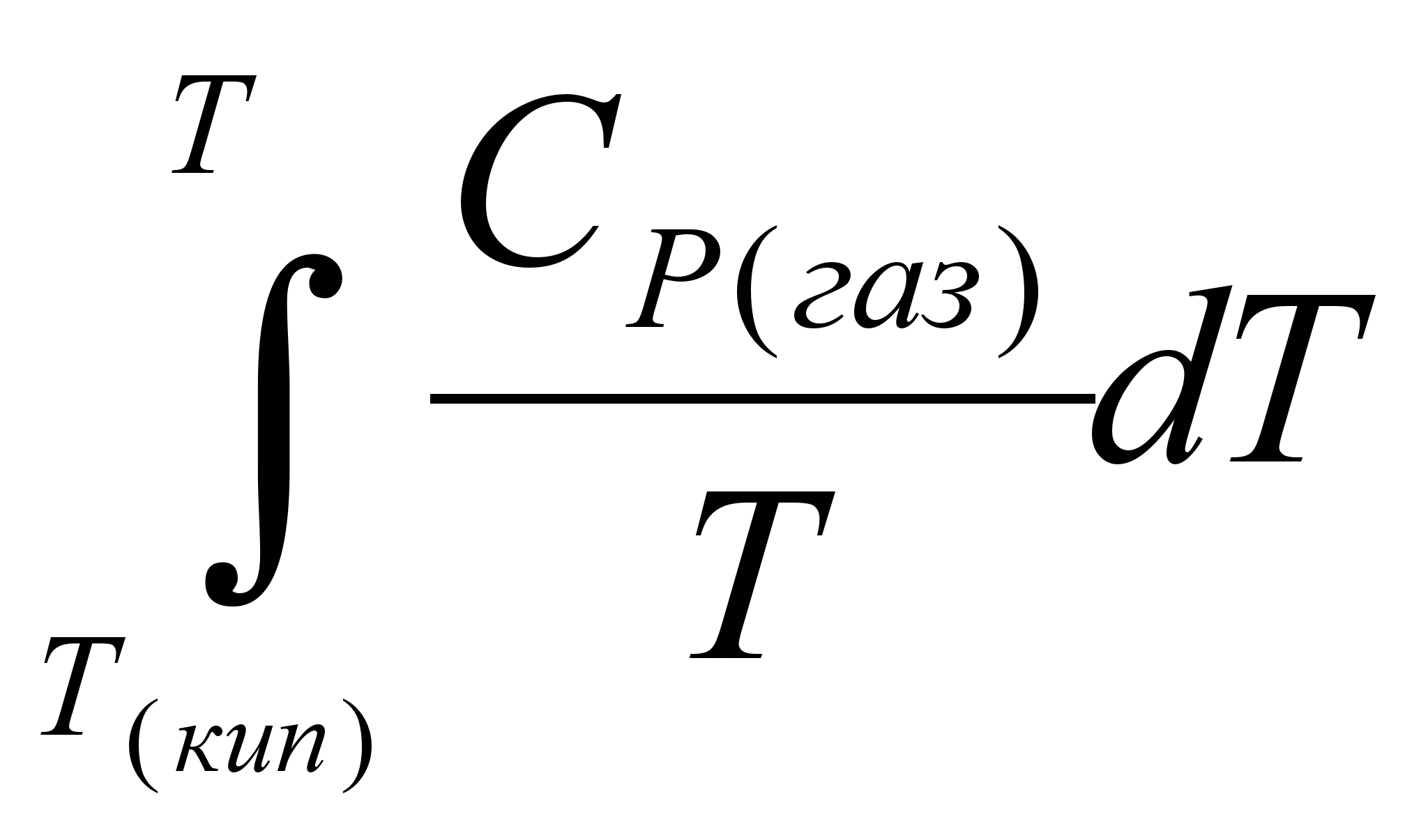 = = 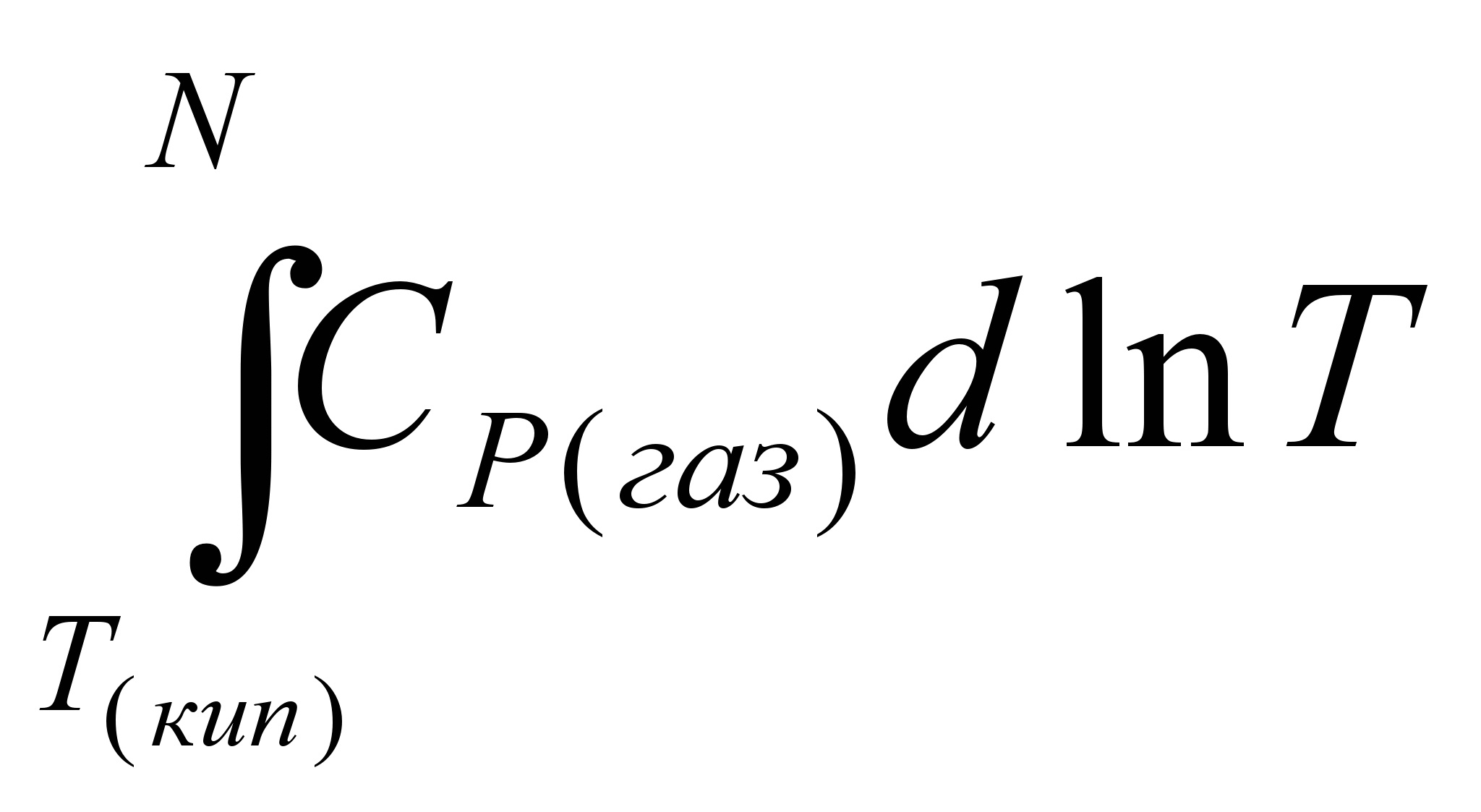 (5.25) (5.25)
Таким образом, абсолютная энтропия тела при температуре Т составит:
ST = ΔS =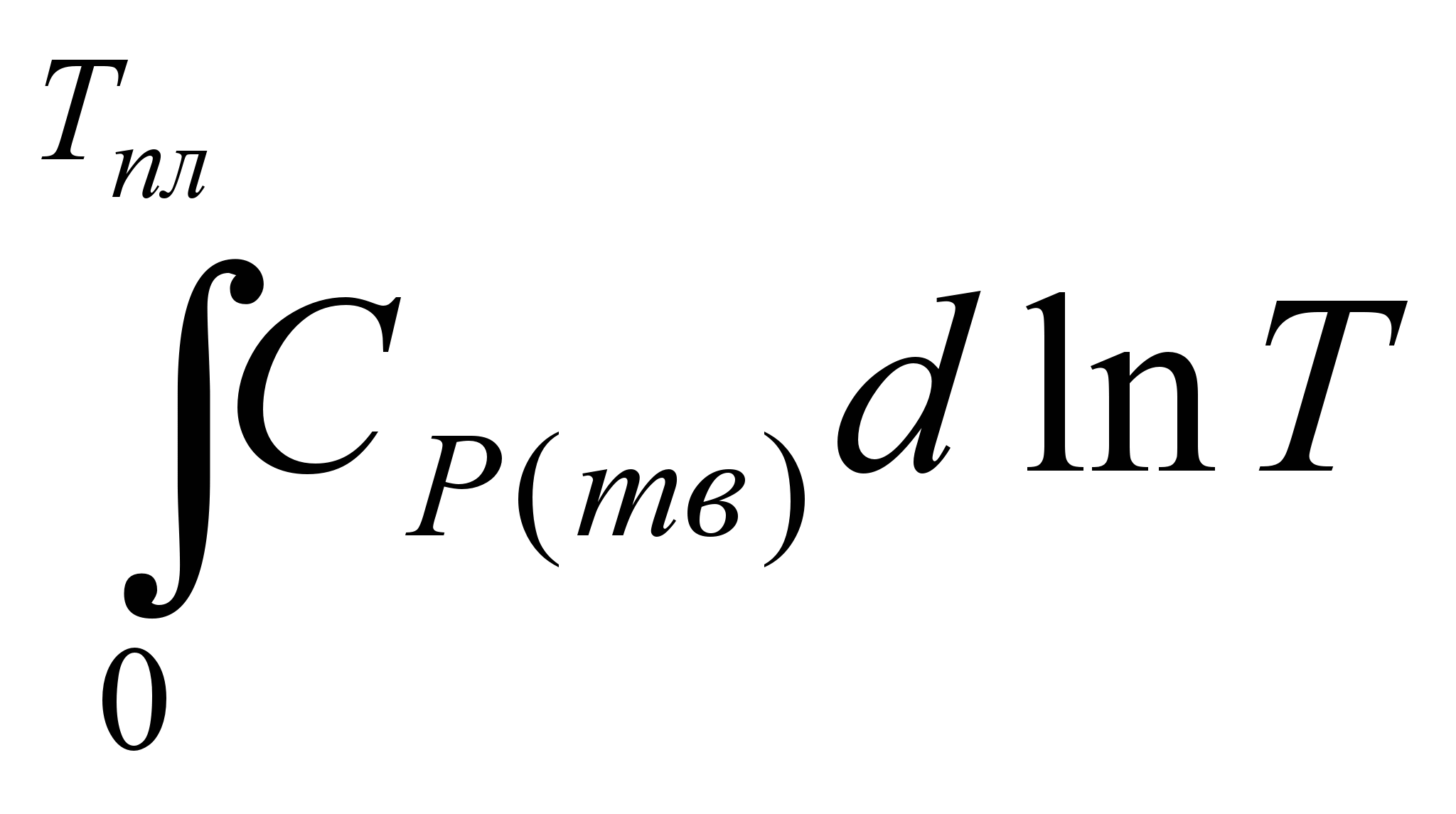 + +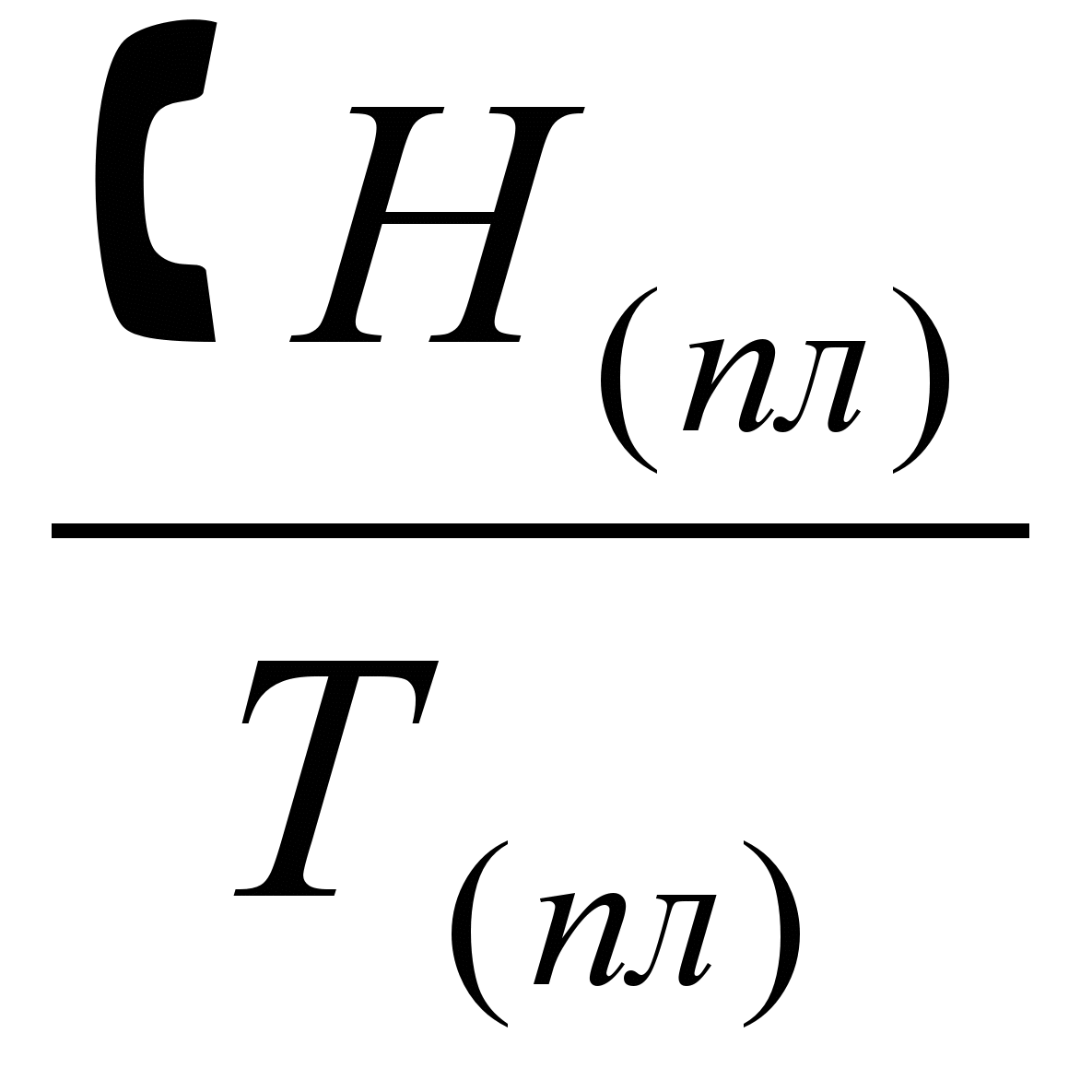 + +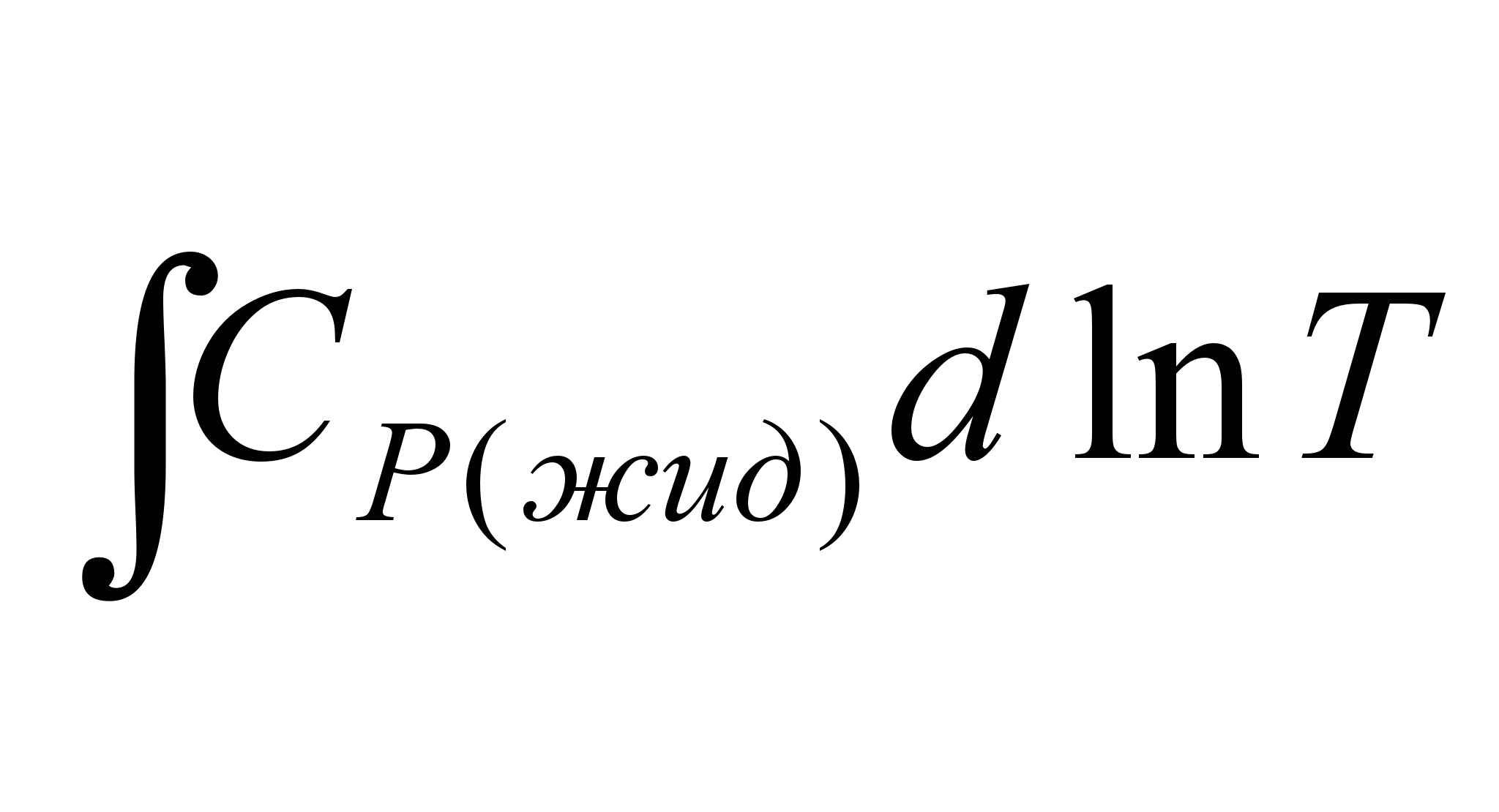 + +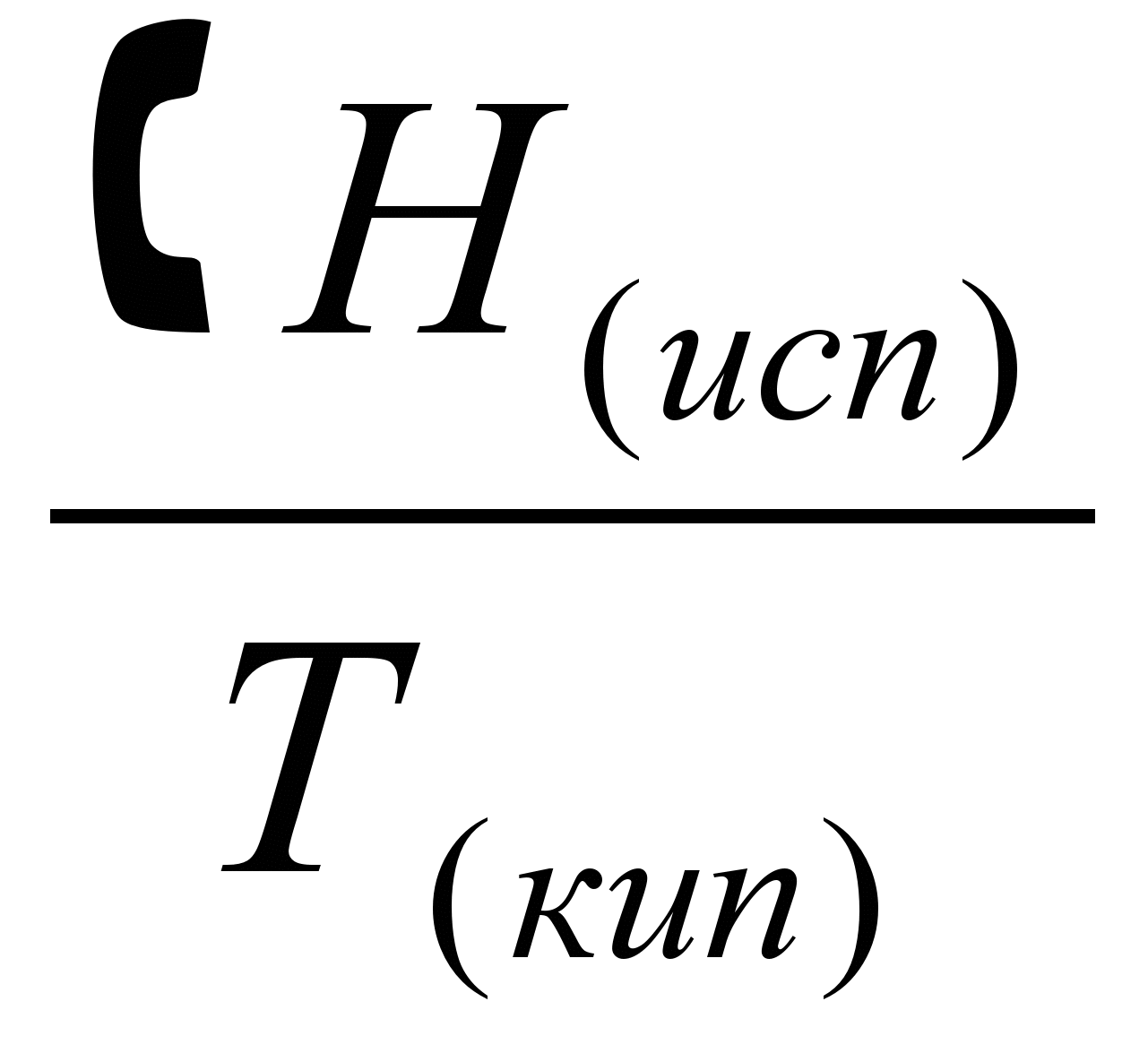 + +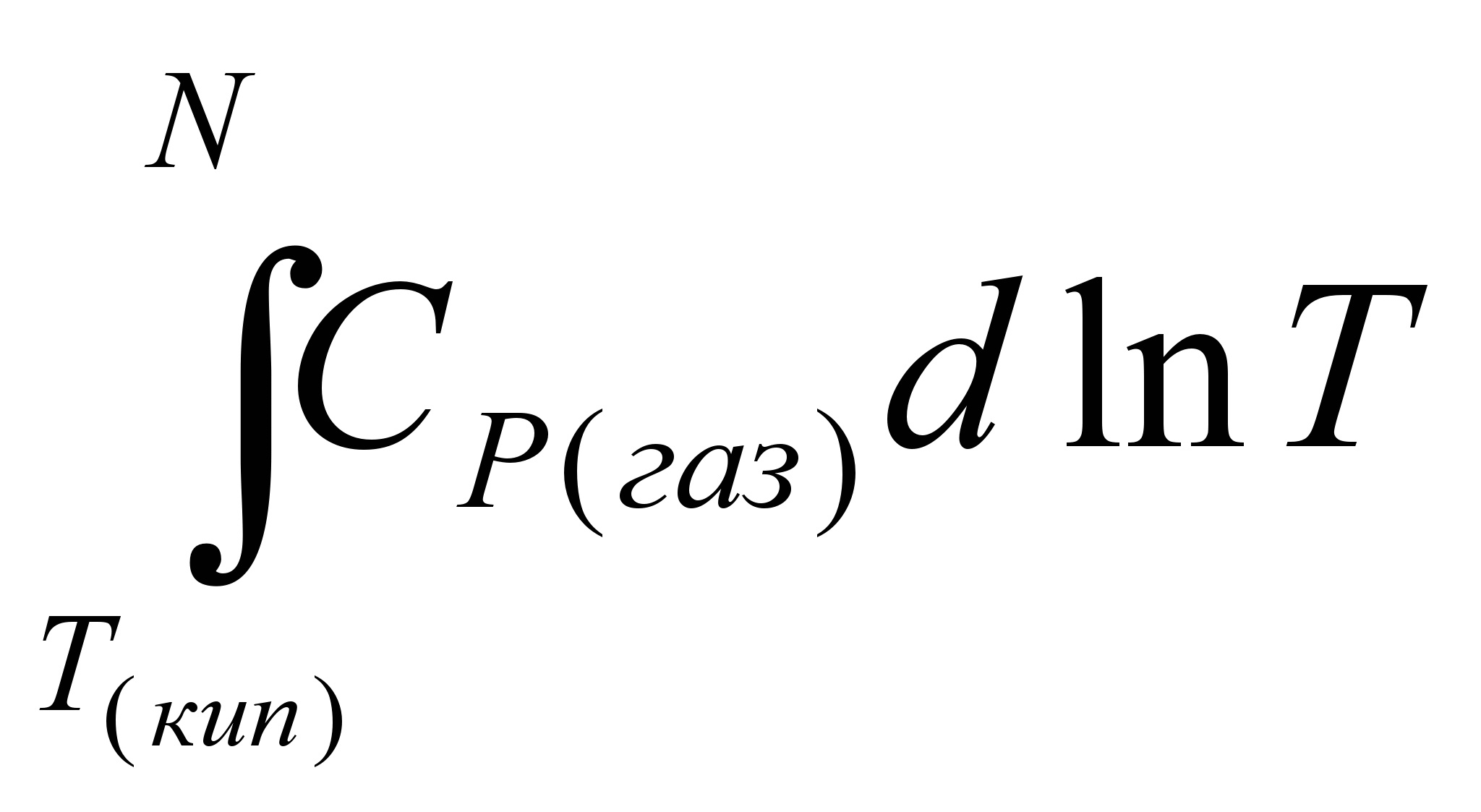 (5.26) (5.26)
Зная температурную зависимость теплоемкости, по уравнению (5.26) можно рассчитать абсолютную энтропию тела при любой температуре. Наиболее надёжным является графический способ определения абсолютной энтропии тела. Для этой цели на основе опытных данных строится график в координатах СР-lnT. Величина площади, которая находится под кривой и которая ограничена крайней ординатой при интересующей нас температуре, соответствует энтропии тела при данной температуре за вычетом энтропий фазовых превращений (Рисунок 5.3).
Ср
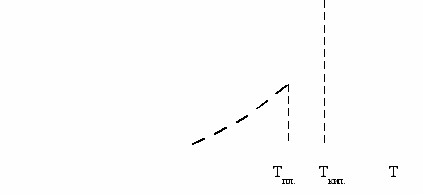
lnT
Рисунок 5.3 - Графический метод определения абсолютного
значения энтропии тела.
В термодинамических таблицах приведены значения абсолютных энтропий тел в стандартных условиях при температуре 298 К. Абсолютную энтропию тела при любой температуре по уравнению:
S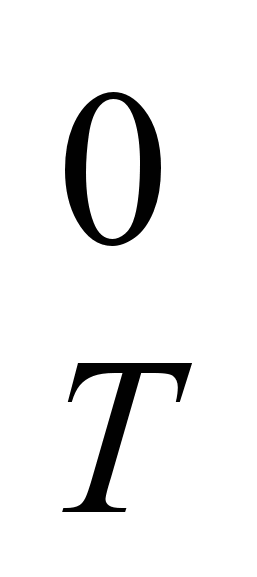 = S = S + + 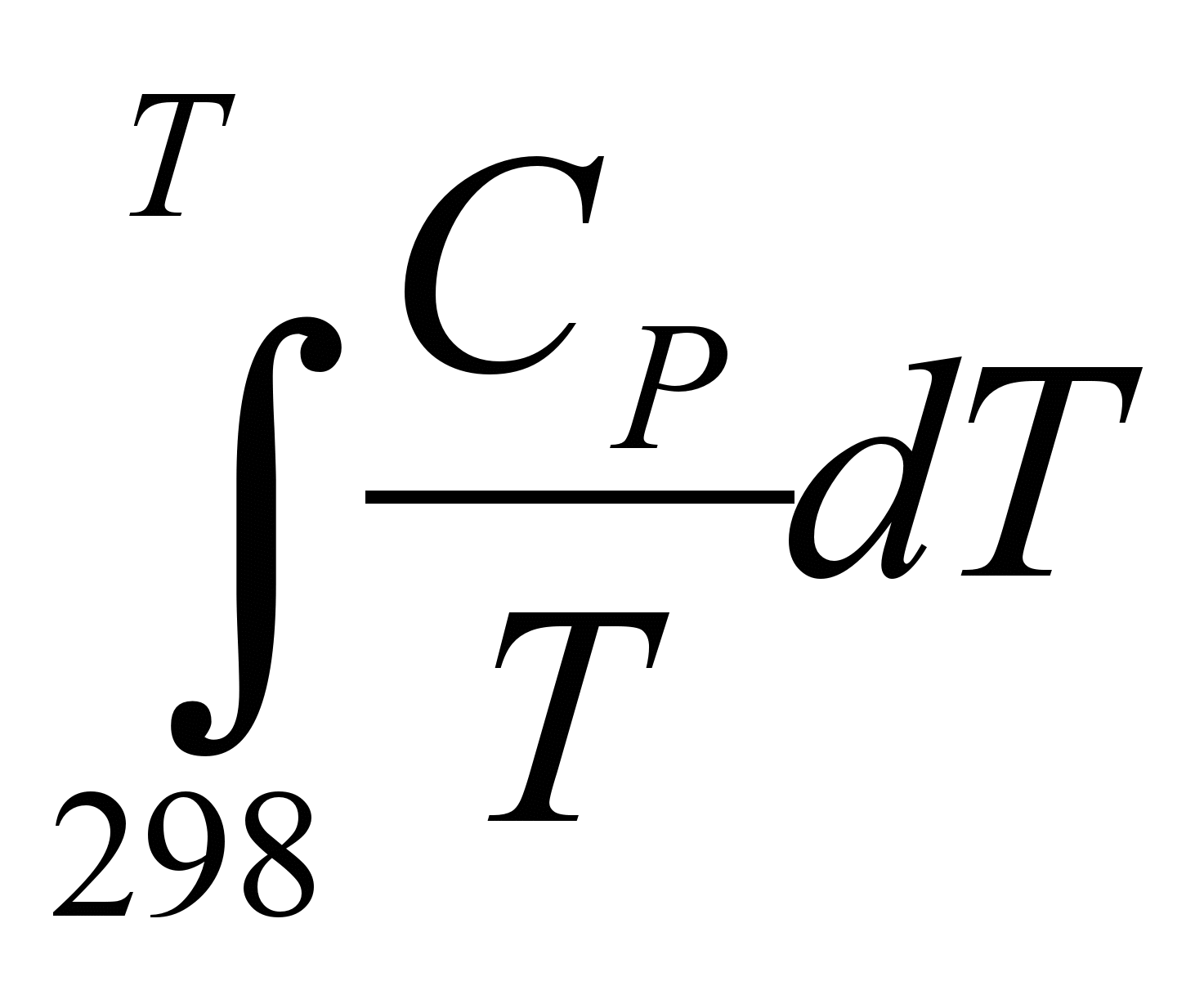 (5.26) (5.26)       
|
|
Постулат Планка. Расчет абсолютной энтропии индивидуального вещества на основании постулата Планка в стандартных условиях ( ). Как найти энтропию газообразного вещества при ). Как найти энтропию газообразного вещества при  и и 
Формулировка
постулата Планка
Энтропия индивидуального кристаллического вещества с идеально построенной кристаллической решеткой при Т = 0
К равна нулю. 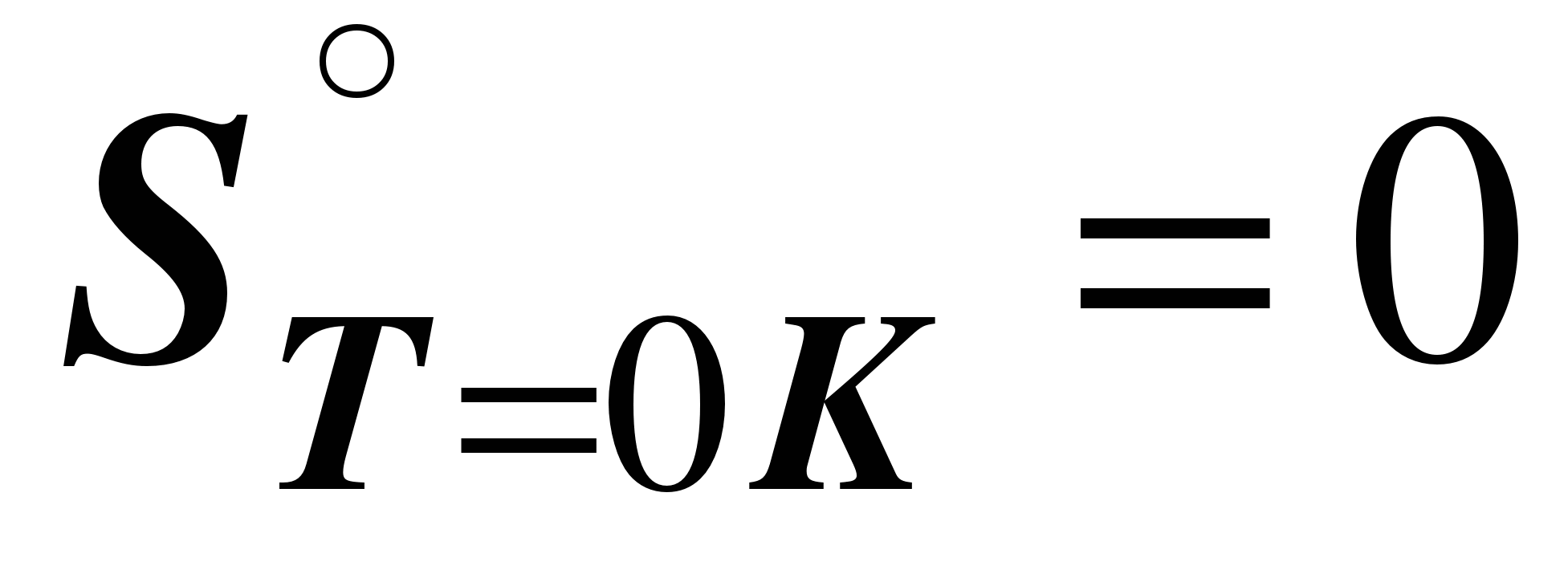 для идеального кристаллического вещества для идеального кристаллического вещества
Замечание
^ Энтропия стеклообразного (некристаллического) вещества и твердых растворов не равна 0 и при Т = 0 К.
Постулат Планка не вытекает из 1-го и 2-го законов термодинамики и не может быть доказан в рамках классической термодинамики
С помощью постулата Планка можно вычислить абсолютную величину энтропиииндивидуального вещества при любой температуре. Эта величина называетсяабсолютной энтропией вещества и обозначается ST°. Абсолютные энтропии большинства веществ рассчитаны и приведены в справочной литературе [4].
Для вычисления абсолютной энтропии газообразного вещества при температуре Tнеобходимо знать:
1.теплоемкость этого вещества в кристаллическом состоянии от температуры плавления (TПЛ.) и до температур, близких к абсолютному нулю;
Измерение теплоемкостей веществ в области низких температур является сложной задачей. В настоящее время методами низкотемпературной калориметрии исследованы многие вещества и получены их низкотемпературные теплоемкости.
2.теплоты фазовых переходов вещества (плавления, испарения и др.) при стандартном давлении;
3.температурные зависимости теплоемкости вещества в жидком состоянии в интервале от TПЛ. до TКИП. и газообразного вещества при температурах вышеTКИП..
Энтропия стеклообразного (некристаллического) вещества и твердых растворов не равна 0 и при Т = 0 К.
Постулат Планка не вытекает из 1-го и 2-го законов термодинамики и не может быть доказан в рамках классической термодинамики.
С помощью постулата Планка можно вычислить абсолютную величину энтропиииндивидуального вещества при любой температуре. Эта величина называетсяабсолютной энтропией вещества и обозначается ST°. Абсолютные энтропии большинства веществ рассчитаны и приведены в справочной литературе [4].
|
|
Для вычисления абсолютной энтропии газообразного вещества при температуре Tнеобходимо знать:
теплоемкость этого вещества в кристаллическом состоянии от температуры плавления (TПЛ.) и до температур, близких к абсолютному нулю;
Измерение теплоемкостей веществ в области низких температур является сложной задачей. В настоящее время методами низкотемпературной калориметрии исследованы многие вещества и получены их низкотемпературные теплоемкости.
теплоты фазовых переходов вещества (плавления, испарения и др.) при стандартном давлении;
температурные зависимости теплоемкости вещества в жидком состоянии в интервале от TПЛ. до TКИП. и газообразного вещества при температурах вышеTКИП..
Предположим 1 моль кристаллического вещества, находящегося при абсолютном нуле (T = 0 K), превращается при постоянном давлении P = 1 атм. в газообразное вещество при температуре T. При этом происходят следующие процессы:
нагревание кристаллического вещества от 0 до TПЛ.;
плавление вещества при постоянной температуре (TПЛ.) и стандартном давлении 1 атм.;
нагревание жидкого вещества от TПЛ. до TКИП.;
испарение жидкости при TКИП. и P = 1 атм.;
нагревание газообразного вещества от TКИП. до T (рис. 1.16).
|
|
Т = 0 K
|
|
TПЛ.
|
|
TКИП.
|
|
T
|
|
|
нагревание
от 0 K доTПЛ.
|
|
нагревание
от TПЛ доTКИП
|
|
нагревание
от TКИП доT
|
|
|
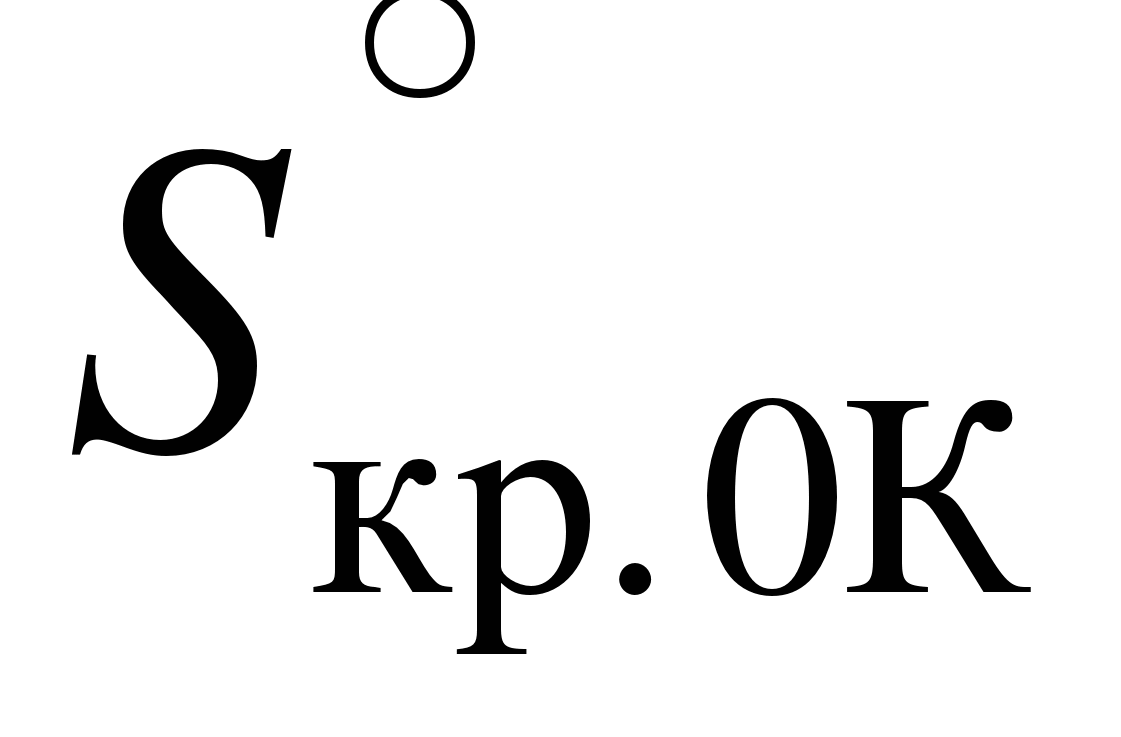
|
|
|
|
|
|
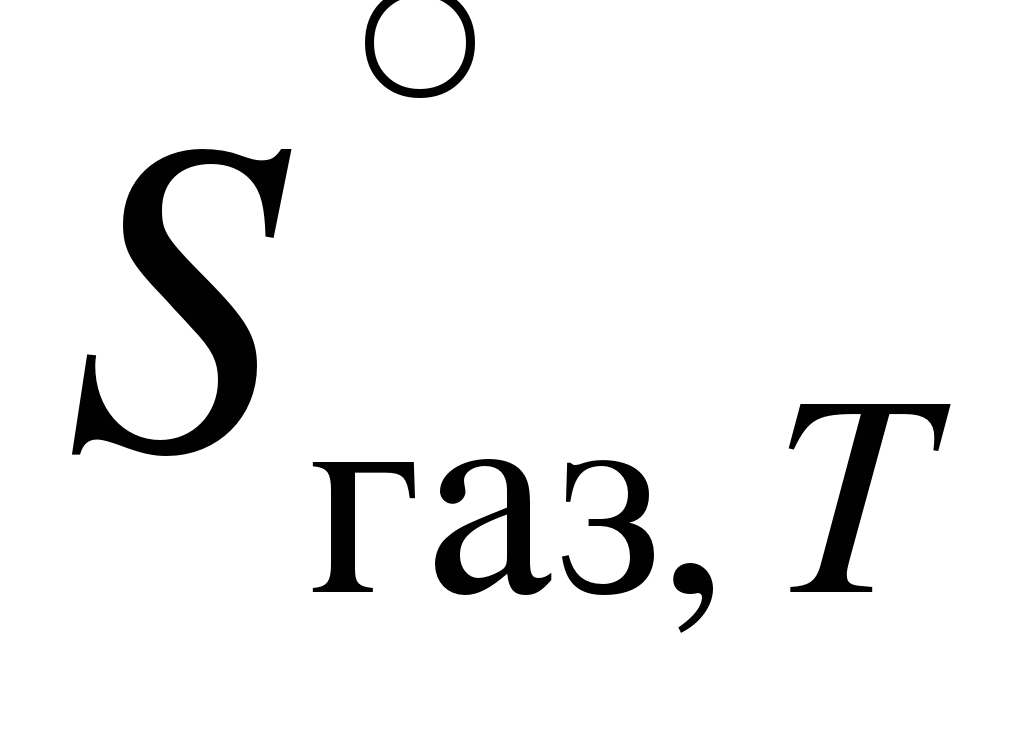
|
|
Рис. 1.16. Схема превращения «абсолютно холодного» кристалла
в «горячий» газ
|
|
Можно вычислить изменение энтропии на каждом этапе превращения и рассчитать прирост энтропии 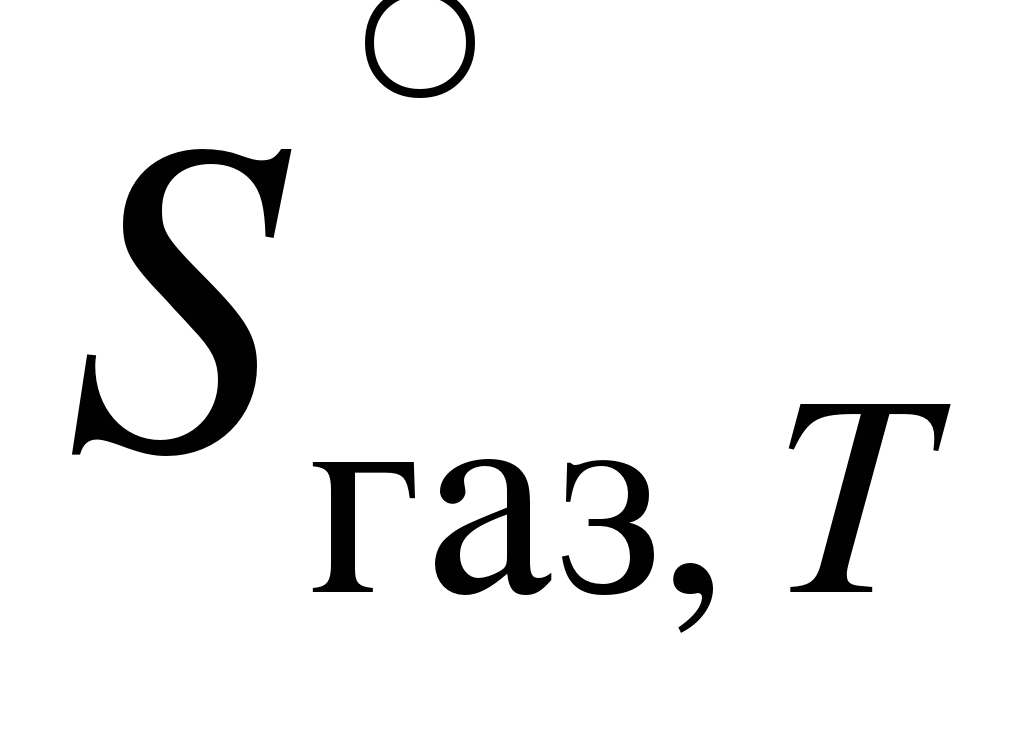 - - 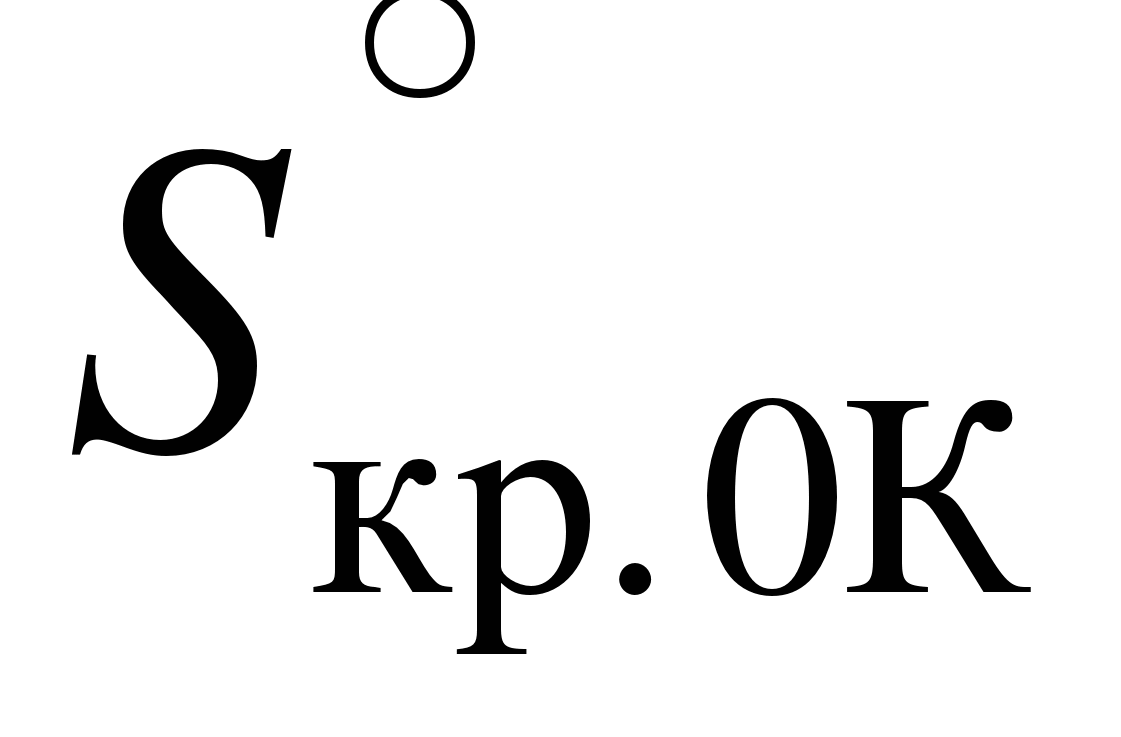 . .
Изменение энтропии при нагревании
|
|
При нагревании n молей вещества от T1 до Т2 при постоянном давлении изменение энтропии можно посчитать по формуле
|
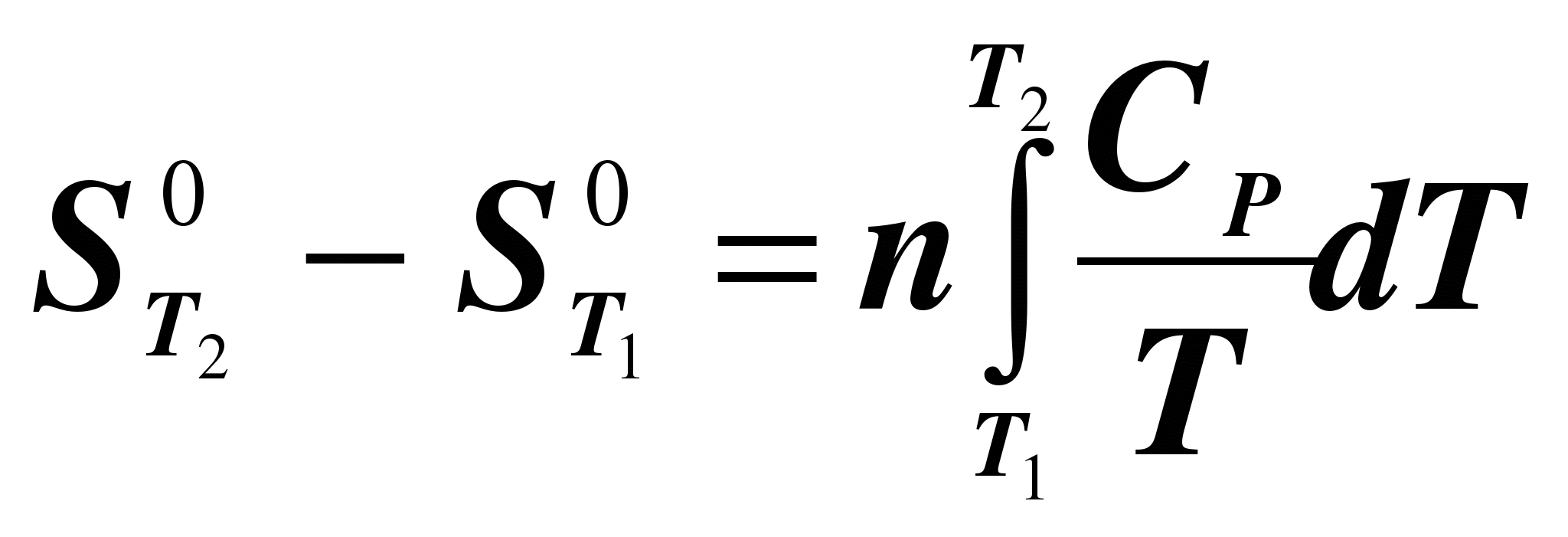 , (1.29) , (1.29)
где 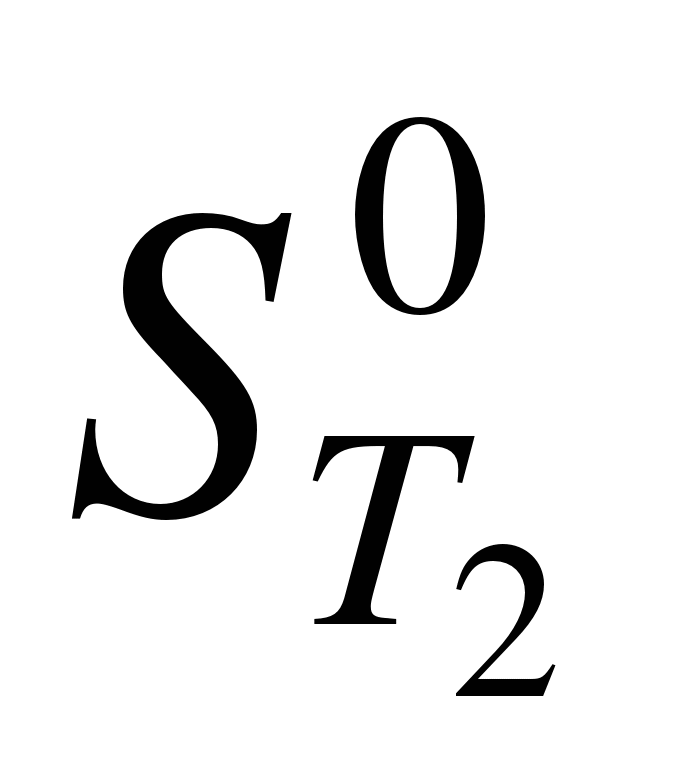 – энтропия вещества при температуре Т2; – энтропия вещества при температуре Т2;
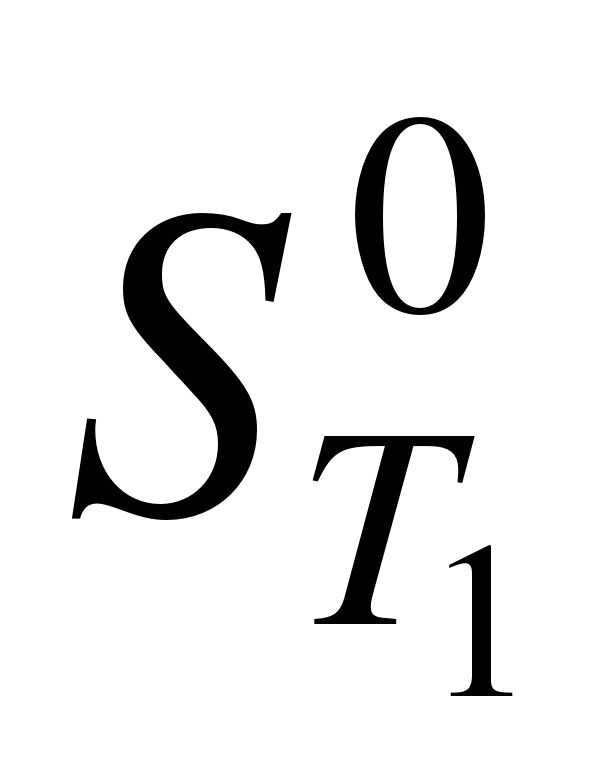 – энтропия вещества при температуре T1; – энтропия вещества при температуре T1;
СP – мольная теплоемкость вещества при постоянном давлении.
|
|
Зависимость энтропии индивидуального вещества от температуры при постоянном давлении. Приведите соответствующее дифференциальное уравнение. Схематически изобразите график этой зависимости в широком температурном интервале, включающем температуры плавления и кипения вещества.
Зная функциональную зависимость теплоемкости от температуры, можно рассчитать значения других термодинамических функций или, по крайней мере, их изменение с температурой. Например, согласно теореме Нернста, гласящей, что энтропия при абсолютном нуле равна нулю, для значения энтропии любого вещества при произвольной температуре получаем формулу:
|
|
|
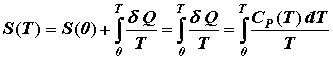
|
.
|
|
|
|
(4.2.1)
|
Т.е., зная температурную зависимость теплоемкости, можно рассчитать абсолютное значение энтропии. Поскольку теплоемкость есть положительная величина, то энтропия естьмонотонно возрастающая функция температуры. Пример реальной температурной зависимости энтропии конкретного вещества показан на рис. 4.2.1.
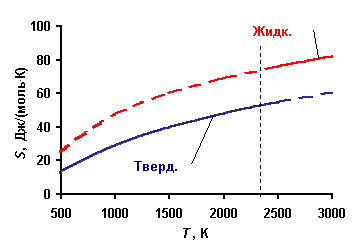
Рис. 4.2.1. Зависимость молярной энтропии твердого и жидкого бора от температуры
Энергия Гиббса, зависимость энергии Гиббса от температуры и давления. Графическое представление и анализ указанных зависимостей.
Зависимость энергии Гиббса от температуры и давления
H – TS U + pV– TS G (7.21)
GpTS, H -T rGpT rH -TrS(7.22)
H характеризует общее изменение энергии системы в ходе процесса, а изменение энергии Гиббса показывает, какая часть ее может быть превращена в полезную работу, поэтому раньше ее называли свободной энергией, в противоположность энтропийному члену, который характеризовал связанную энергию, недоступную для превращения в работу.
а)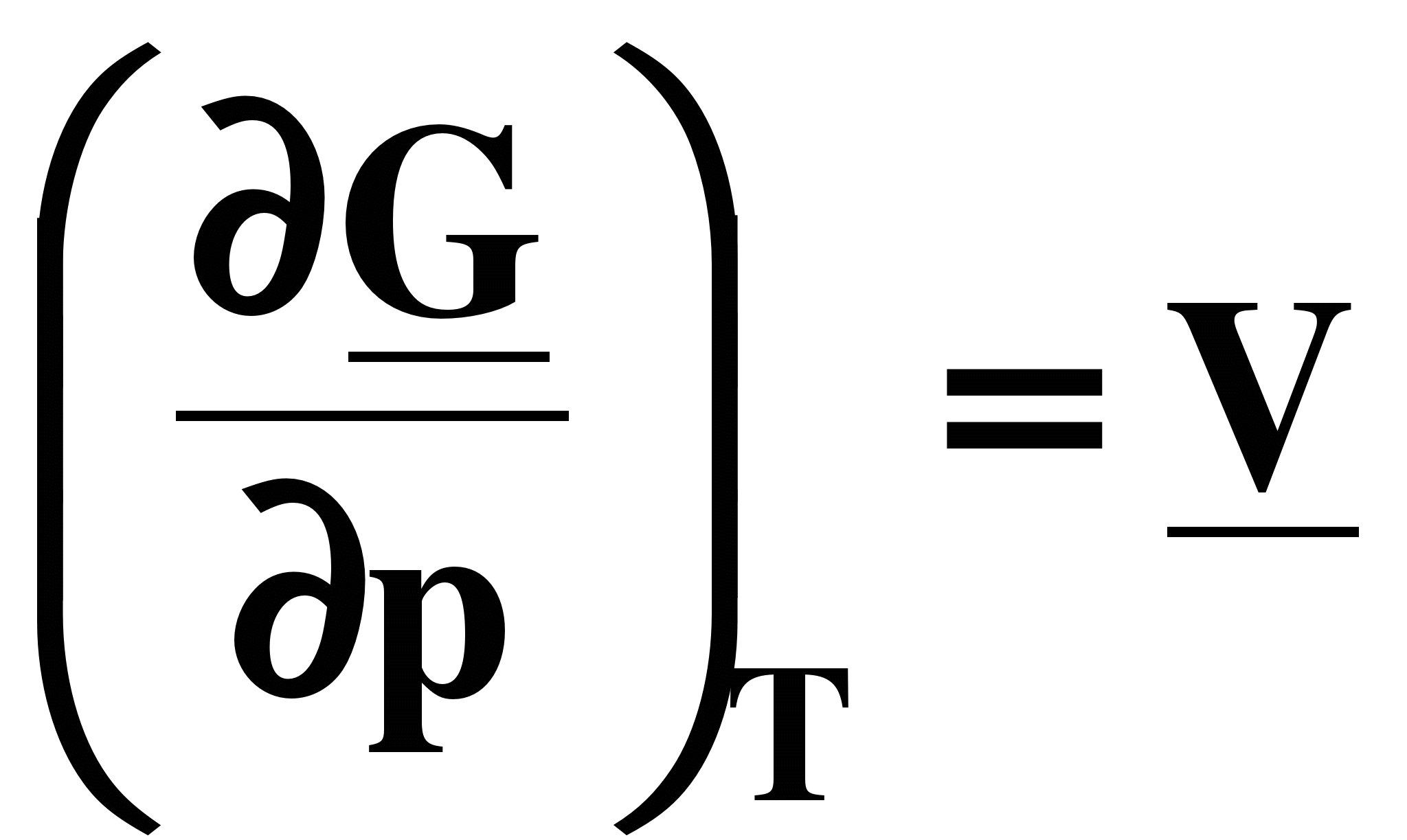 ; б) ; б) 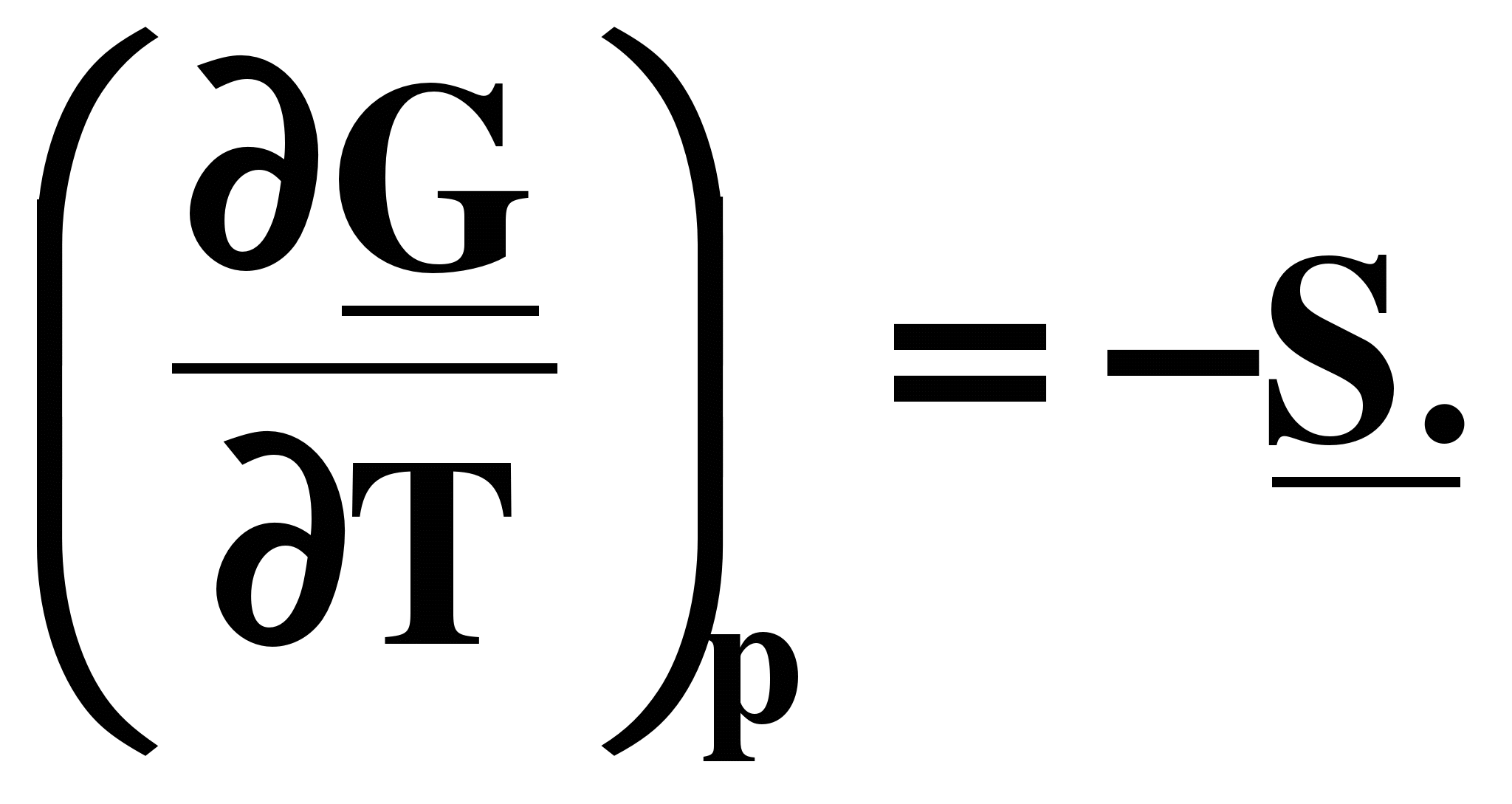 (7.20) (7.20)
Из уравнения 7.20а следует, что с ростом давления энергия Гиббса увеличивается, так как V> 0, но темп роста замедляется, так как объем постепенно уменьшается. Причем для разных идеальных газов эти кривые будут одинаковыми.
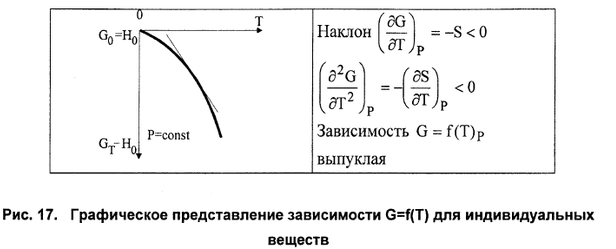 
Рис. 7.1. Зависимость энергии Гиббса от давления и температуры.
С ростом температуры энергия Гиббса убывает, так как энтропия всегда положительна, причем падение энергии Гиббса будет ускоряться из-за роста энтропии при повышении температуры.
Энергия Гельмгольца. Зависимость энергии Гельмгольца от ее естественных переменных (V и T). Графическое представление указанных зависимостей. Расчет  в процессах нагревания и расширения идеального газа. в процессах нагревания и расширения идеального газа.
  
Энтропия, энергия Гиббса и энергия Гельмгольца как критерии состояния равновесия и направления процессов.
|
 Скачать 2.79 Mb.
Скачать 2.79 Mb.