Основы химической термодинамики

Название	Основы химической термодинамики
Анкор	PC1E2010.rtf
Дата	02.02.2017
Размер	2.79 Mb.
Формат файла
Имя файла	PC1E2010.rtf
Тип	Документы #1881
страница	4 из 7

1 2 3 4 5 6 7

Для некоторой реакции сумма теплоемкостей исходных веществ меньше суммы теплоемкостей продуктов. Причем при повышении температуры Δ_rС_р увеличивается. Изобразите схематически графики зависимости

для исходных веществ и продуктов реакции и теплового эффекта реакции от температуры. Приведите краткое теоретическое обоснование ответа и соответствующие математические выражения.

Второе начало термодинамики. Энтропия, изменение энтропии в термодинамических процессах с участием идеального газа при

.

Существуют несколько эквивалентных формулировок второго начала термодинамики:

Постулат Клаузиуса: «Невозможен процесс, единственным результатом которого являлась бы передача тепла от более холодного тела к более горячему» (такой процесс называется процессом Клаузиуса).

Постулат Томсона: «Невозможен круговой процесс, единственным результатом которого было бы производство работы за счет охлаждения теплового резервуара» (такой процесс называется процессом Томсона).

Эквивалентность этих формулировок легко показать. В самом деле, допустим, что постулат Клаузиуса неверен, то есть существует процесс, единственным результатом которого была бы передача тепла от более холодного тела к более горячему. Тогда возьмем два тела с различной температурой (нагреватель и холодильник) и проведем несколько циклов тепловой машины забрав тепло у нагревателя, отдав холодильнику и совершив при этом работу . После этого воспользуемся процессом Клаузиуса и вернем тепло от холодильника нагревателю. В результате получается, что мы совершили работу только за счет отъёма теплоты от нагревателя, то есть постулат Томсона тоже неверен.

С другой стороны, предположим, что неверен постулат Томсона. Тогда можно отнять часть тепла у более холодного тела и превратить в механическую работу. Эту работу можно превратить в тепло, например, с помощью трения, нагрев более горячее тело. Значит, из неверности постулата Томсона следует неверность постулата Клаузиуса.
Таким образом, постулаты Клаузиуса и Томсона эквивалентны.
Другая формулировка второго начала термодинамики основывается на понятии энтропии:
«Энтропия изолированной системы не может уменьшаться» (закон неубывания энтропии).

Такая формулировка основывается на представлении об энтропии как о функции состояния системы, что также должно быть постулировано.

В состоянии с максимальной энтропией макроскопические необратимые процессы (а процесс передачи тепла всегда является необратимым из-за постулата Клаузиуса) невозможны. $c:\documents and settings\admin\рабочий стол\b00001882-62.png$ $c:\documents and settings\admin\рабочий стол\b00001882-63.png$

Второе начало термодинамики. Энтропия. Зависимость энтропии от температуры и давления. Изменение энтропии в процессах с участием идеального газа.

Существуют несколько эквивалентных формулировок второго начала термодинамики:

Постулат Клаузиуса: «Невозможен процесс, единственным результатом которого являлась бы передача тепла от более холодного тела к более горячему» (такой процесс называется процессом Клаузиуса).

Постулат Томсона: «Невозможен круговой процесс, единственным результатом которого было бы производство работы за счет охлаждения теплового резервуара» (такой процесс называется процессом Томсона).

Эквивалентность этих формулировок легко показать. В самом деле, допустим, что постулат Клаузиуса неверен, то есть существует процесс, единственным результатом которого была бы передача тепла от более холодного тела к более горячему. Тогда возьмем два тела с различной температурой (нагреватель и холодильник) и проведем несколько циклов тепловой машины забрав тепло у нагревателя, отдав холодильнику и совершив при этом работу . После этого воспользуемся процессом Клаузиуса и вернем тепло от холодильника нагревателю. В результате получается, что мы совершили работу только за счет отъёма теплоты от нагревателя, то есть постулат Томсона тоже неверен.

С другой стороны, предположим, что неверен постулат Томсона. Тогда можно отнять часть тепла у более холодного тела и превратить в механическую работу. Эту работу можно превратить в тепло, например, с помощью трения, нагрев более горячее тело. Значит, из неверности постулата Томсона следует неверность постулата Клаузиуса.
Таким образом, постулаты Клаузиуса и Томсона эквивалентны.
Другая формулировка второго начала термодинамики основывается на понятии энтропии:
«Энтропия изолированной системы не может уменьшаться» (закон неубывания энтропии).

Такая формулировка основывается на представлении об энтропии как о функции состояния системы, что также должно быть постулировано.

В состоянии с максимальной энтропией макроскопические необратимые процессы (а процесс передачи тепла всегда является необратимым из-за постулата Клаузиуса) невозможны

Энтропия системы является функцией ее состояния, определенная с точностью до произвольной постоянной.
Если система совершает равновесный переход из состояния 1 в состояние 2, то изменение энтропии

(6.2.1)

       Таким образом, по формуле (6.2.1) можно определить энтропию лишь с точностью до аддитивной постоянной, т.е. начало энтропии произвольно. Физический смысл имеет лишь разность энтропий.
       Исходя из этого, найдем изменения энтропии в процессах идеального газа.
       Так как при Т = const,

, или

(6.2.2)

Таким образом, изменение энтропии ΔS_1-2 идеального газа при переходе его из состояния 1 в состояние 2 не зависит от вида перехода 1 - 2.
Каждый из изопроцессов идеального газа характеризуется своим изменением энтропии, а именно:

изохорический: , т.к. ;
изобарический: т.к. Р₁ = Р₂;
изотермический: т.к. ;
адиабатический: , т.к.

Отметим, что в последнем случае адиабатический процесс называют изоэнтропийным процессом, т.к. .

Второе начало термодинамики. Энтропия. Изменение энтропии в процессе смешения идеальных газов.

(6.2.1)

$c:\documents and settings\admin\рабочий стол\физхим\b00001882-62 (1).png$ $c:\documents and settings\admin\рабочий стол\физхим\b00001882-63.png$

Самопроизвольные и несамопроизвольные процессы. Второе начало термодинамики. Математическое выражение 2-го закона термодинамики. Изменение энтропии в самопроизвольном процессе, протекающем в изолированной системе.

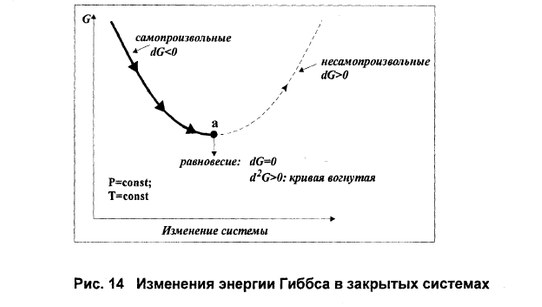
Второе начало термодинамики, которое, как и первое постулируется на основании многовекового человеческого опыта, дает возможность предсказать направление процессов. Именно второе начало позволяет разделить все процессы, которые возможны с точки зрения первого закона термодинамики, на две различные группы: самопроизвольные и несамопроизвольные.

Самопроизвольные процессы – это неравновесные процессы, которые протекают без воздействия внешней силы в направлении достижения равновесия. Для проведения самопроизвольных процессов не только не затрачивается работа, но при соответствующих условиях эта система сама может произвести работу в количестве, пропорциональном происходящему изменению. Примерами самопроизвольных процессов могут служить переход тепла от более нагретого тела к менее нагретому, смешение газов, расширение газов в вакуум, превращение кинетической энергии движущегося тела в тепло и т.д. Все перечисленные процессы протекают в направлении, приближающем систему к равновесию.

Обратные по направлению процессы: переход тепла от холодного тела к горячему, разделение газовой смеси, сжатие газа и т.д. удаляют соответствующие системы от равновесия и без внешнего воздействия происходить не могут, т.е. для проведения таких процессов необходимо затратить работу в количестве, пропорциональном происходящим изменениям. Такие процессы называются несамопроизвольные.

Рассмотренные ранее равновесные процессы, при которых системы, бесконечно медленно изменяясь, проходят непрерывный ряд равновесных состояний, можно рассматривать в качестве промежуточных между процессами самопроизвольными и несамопроизвольными.

Самопроизвольные процессы

Равновесные процессы

Несамопроизвольные процессы

Для получения математического выражения второго начала термодинамики рассмотрим работу идеальной тепловой машины (машины, обратимо работающей без трения и потерь тепла; рабочее тело – идеальный газ). Работа машины основана на принципе обратимого циклического процесса – термодинамического цикла Карно (рис. 1.2).

  Формулировки второго закона термодинамики. Закон прошел длительный путь эволюции и сначала был сформулирован как основной закон действия тепловых машин

5.2.1.  Теорема Карно (1824) “Размышление о движущей силе огня” – коэффициент полезного действия обратимого цикла, состоящего  из 2 изотерм и 2 адиабат, зависит только от разности температур тепловых резервуаров и не зависит от природы рабочего тела

 = (Q₁– Q₂)/Q₁= (T₁–T₂)/T₁= 1 – Т₂/Т₁.(5.1)

5.2.2.  Томсон (лорд Кельвин) (1848) ввел понятие абсолютной температуры и (1851) сформулировал 2 закон ТД – невозможно построить периодически действующую тепловую машину, которая только бы черпала тепло из одного резервуара и производила механическую работу, т.е. невозможен вечный двигатель 2-го рода

5.2.3.  Клаузиус (1850)  дал первую формулировку 2 закона ТД – невозможен самопроизвольный переход теплоты от тела менее нагретого к телу более нагретому.Обе формулировки эквивалентны, одна невозможна без другой. (1854) Ввел понятие энтропии.

5.2.4.  Математическое выражение 2 –го закона ТД

Для каждой фазы , содержащей k компонентов, существует аддитивная функция состояния, называемая энтропией

S^  = S^(U^, V^, n₁^, n^₂ , ..n^_k);     ,  S  = ,  S = S₂ – S₁

     изменение которой следующим образом связано с теплотой и температурой процессар

dS =  для обратимых процессов;  (5.1)

dS >    для необратимых процессов. (5.2)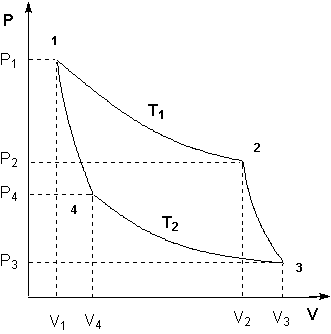

http://gendocs.ru/docs/29/28970/conv_1/file1_html_m15fc96da.png

      Рис. 5.1. К понятию энтропии.  (цикл Карно)

Температура – интегрирующий делитель, который превратил функцию процесса в изменение функции состояния, а энтропия – тепловая координата.

     Работу всегда можно выразить как произведение интенсивного параметра на изменение экстенсивного

W= - ,                                         (5.3),

а теплоту – аналогично         Q = TdS  – для обратимых процессов,    (5.4)

где Т – интенсивный параметр, а dS изменение экстенсивного свойства.

     Объединяя 1 и 2 законы термодинамики (уравнения  2.2  и  5.1),  получаем

    d U = TdS – pdV + .                           (5.5)

.  Анализ уравнений типа (5.5) привел Каратеодори к новой формулировке    2-го закона термодинамики, не связанной с тепловыми машинами:

вблизи любого состояния термически однородной и адиабатически изолированной  системы есть бесконечное множество других состояний, не достижимых адиабатическим путем. В этом случае Т становится интегрирующим делителем, а S – функцией состояния.

На основе анализа работы идеальной тепловой машины Карно можно сделать следующий вывод, являющийся также одной из формулировок второго начала термодинамики:

^ Любая форма энергии может полностью перейти в теплоту, но теплота преобразуется в другие формы энергии лишь частично.
самопроизвольно в изолированной системе протекают те процессы, которые приводят к возрастанию энтропии системы. Таким образом, второй закон термодинамики гласит: «Если в изолированной системе протекают самопроизвольные процессы, то ее энтропия возрастает» (закон возрастания энтропии).

Если энтропия системы в исходном состоянии может быть выражена как: S₁ = RlnV₁, а в конечном состоянии S₂lnV=R₂S = S, то изменение энтропии в результате протекания обратимого процесса ₂ – S₁ =

или

S/обратимого процесса/ =

Соответственно для необратимого процесса

S/необратимого процесса/ >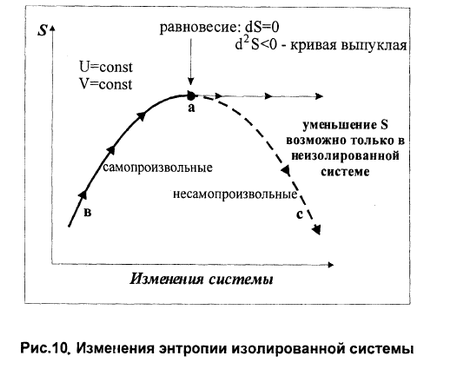

$c:\documents and settings\admin\рабочий стол\физхим\b00001882-60.png$

Термодинамически обратимые и необратимые, самопроизвольные и несамопроизвольные процессы. Формулировки и математическое выражение второго начала термодинамики.

Второй закон термодинамики, в отличие от первого закона термодинамики, изучает все процессы, которые протекают в природе, и эти процессы можно классифицировать следующим образом.

Процессы бывают самопроизвольные, несамопроизвольные, равновесные, неравновесные.Самопроизвольные процессы делятся на обратимыеи необратимые.Второй закон термодинамики называют законом направленности процесса в изолированной системе (закон роста S). Обратимые и необратимые процессы

Необратимые процессыидут без затраты работы, протекают самопроизвольно лишь в одном направлении, это такие изменения состояния в изолированной системе, когда при обращении процессов свойства всей системы меняются. К ним относятся:

1) теплопроводность при конечной разности температур;

2) расширение газа при конечной разности давлений;

3) диффузия при конечной разности концентраций.

Обратимыми процессамив изолированной системе называются такие процессы, которые можно обратить без каких-либо изменений в свойствах этой системы.

Обратимые:механические процессы в системе, где отсутствует трение (идеальная жидкость, ее движение, незатухающие колебания маятника в вакууме, незатухающие электромагнитные колебания и распространение электромагнитных волн там, где нет поглощения), которые могут возвратиться в начальное состояние.

Самопроизвольные– процессы, которые идут сами собой, на них не затрачивается работа, они сами могут производить ее (движение камней в горах, Na с большой скоростью движется по поверхности, так как идет выделение водорода проверить.).

Несамопроизвольные– процессы, которые не могут идти сами собой, на них затрачивается работа.

Равновесие делится на устойчивое, неустойчивоеи безразличное.

Формулировки второго закона термодинамики. Закон прошел длительный путь эволюции и сначала был сформулирован как основной закон действия тепловых машин

Теорема Карно (1824) “Размышление о движущей силе огня” – коэффициент полезного действия обратимого цикла, состоящего из 2 изотерм и 2 адиабат, зависит только от разности температур тепловых резервуаров и не зависит от природы рабочего тела

 = (Q₁– Q₂)/Q₁= (T₁–T₂)/T₁= 1 – Т₂/Т₁.(5.1)

Томсон (лорд Кельвин) (1848) ввел понятие абсолютной температуры и (1851) сформулировал 2 закон ТД – невозможно построить периодически действующую тепловую машину, которая только бы черпала тепло из одного резервуара и производила механическую работу, т.е. невозможен вечный двигатель 2-го рода

5.2.3. Клаузиус (1850) дал первую формулировку 2 закона ТД – невозможен самопроизвольный переход теплоты от тела менее нагретого к телу более нагретому.Обе формулировки эквивалентны, одна невозможна без другой. (1854) Ввел понятие энтропии.

при обратимом процессе имеет место равенство Клаузиуса:

;

(6.5.1)

при необратимом процессе имеет место неравенство Клаузиуса:

(6.5.2)

Тогда для произвольного процесса,

(6.5.3)

где знак равенства – для обратимого процесса; знак больше - для необратимого.

Значит для замкнутой системы

(6.5.4)

Это выражение – математическая запись второго начала термодинамики.

Выражения (6.5.1) и (6.5.2) можно объединить:

(6.5.5)

Энтропия замкнутой системы при любых происходивших в ней процессах не может убывать (или увеличивается, или остается неизменной)Как следует из соотношения (4.42), для обратимого цикла Карно справедливо равенство

(4.43)

из которого следует:

.	(4.44)
Рис. 4.17

Отношение количества теплоты, полученного системой в изотермическом процессе, к температуре этого процесса называется приведенной теплотой. Следовательно, из соотношения (4.44) видно, что приведенная теплота при переходе системы из состояния 1 в состояние 3 по пути 1→2→3 (рис. 4.17) равна приведенной теплоте при переходе системы из состояния 1 в состояние 3 по пути 1→4→3.Энтропия, как и энергия, присуща любой термодинамической системе, а не только системе, совершающей цикл Карно.

Напомним, что тепло, отданное системой, мы условились считать отрицательным. С учетом этого равенство (4.44) можно представить в виде:

(4.45)

Из соотношения (4.45) следует, что сумма приведенных теплот системы, совершившей круговой равновесный процесс, равна нулю.

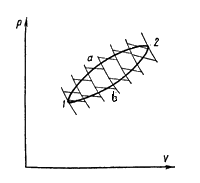
http://ido.tsu.ru/schools/physmat/data/res/molek/uchpos/text/img4_14/image012_1.gif

Рис. 4.18

Обобщим это утверждение, полученное для цикла Карно, на произвольный равновесный круговой процесс, осуществляемый по пути 1а2b'1'.

Проведем ряд бесконечно близких адиабат, пересекающих линии прямого а и обратного b переходов (рис. 4.18). Эти линии разобьются на ряд бесконечно малых отрезков. Через середину каждого отрезка проведем изотермы. Тогда каждую из линий а и b можно считать состоящей из ряда бесконечно близких изотерм. Таким образом, рассматриваемый произвольный цикл представляется совокупностью циклов Карно с переменными температурами нагревателей и холодильников для каждого элементарного цикла.

Обозначим температуры, соответствующие изотермам расширения Т₁, Т₂, … Т_n, а температуры изотерм на стадии сжатия – . Количества теплоты, получаемые системой в процессе расширения на соответствующих участках элементарных циклов Карно, обозначим , а количества теплоты, отдаваемые системой на стадии сжатия – .

Количества теплоты ΔQ_i и ΔQ'_i (i = 1, 2, … n) система получала соответственно при температурах T_i и отдавала при температурах T'_i. Это, следовательно, теплоты изотермических процессов.

На основании равенства (4.45) для каждого элементарного цикла Карно справедливо

(4.46)

Суммирование правых и левых частей полученного равенства (4.46) приводит к результату:

(4.47)

Полученное соотношение означает, что суммы приведенных теплот перехода системы из состояния 1 в состояние 2 по пути а и по пути b равны друг другу. Следовательно, сумма приведенных теплот не зависит от пути перехода системы из одного состояния в другое, поэтому она представляет собой изменение функции состояния, которая и была названа Клаузиусом энтропией. Эту функцию обозначают буквой S, а ее изменение – ΔS. Таким образом,

(4.48)

Следовательно, на основании проведенного обобщения для любого кругового равновесного процесса на основании (4.45) можно записать:

(4.49)

(4.50)

Уравнение (4.50) является математической формулой записи второго начала термодинамики для обратимых процессов.

Рассмотрим теперь необратимый процесс. Согласно (4.42) имеем:

,
или .

(4.51)

Отсюда

(4.52)

Это означает, что энтропия системы, совершающей необратимый процесс, возрастает.

Возрастание энтропии может служить мерой необратимости процессов.

Второе начало термодинамики, математическое выражение для обратимых и необратимых (самопроизвольных) процессов. Энтропия как критерий равновесия и направления самопроизвольного протекания процесса в изолированной системе.

Мы приведем математическую формулировку второго закона термодинамики в форме, удобной для исследования химических и физических превращений в системе. Рис. 1.15. Схема термодинамического превращения Если термодинамическая система переходит из состояния 1, характеризующегося параметрами P₁, V₁, T₁ и функциями состояния U₁,H₁, S₁, F₁, G₁ в состояние 2, характеризующееся параметрами P₂, V₂, T₂ и функциями состояния U₂, H₂, S₂, F₂, G₂, самопроизвольно
равновесным путем, то , (1.27)	неравновесным путем, то , (1.28)
где Q – теплота процесса, протекающего в системе.

Второй закон термодинамики является постулатом, сформулированным на основе накопленного человечеством опыта; доказательством его справедливости служит то, что все выводы, вытекающие из него, находят экспериментальное подтверждение, и до сих пор не произошло ничего, что «запрещает» второй закон термодинамики.
Из второго закона термодинамики путем несложных математических преобразований можно получить ряд следствий, которыми удобно пользоваться для определения направления процесса и условий, при которых в системе наступает равновесие.

Термодинамическая система называется изолированной, если ее объем постоянен и она не обменивается с окружающей средой энергией и веществом.

Если обратиться к схеме, приведенной на рис. 1.15 (см. стр. 30), то для изолированной системы:

V₁ = V₂ = V = const U₁ = U₂ = U = const

Критерием самопроизвольного протекания процесса в изолированной системе является энтропия.
^ В изолированной системе могут самопроизвольно протекать только те процессы, которые приводят к возрастанию энтропии в системе. Когда энтропия достигнет максимального при данных U и V значения, все процессы прекратятся, и система достигнет равновесного состояния.

Итак,
если U = const и V = const, то при самопроизвольном процессе, протекающем неравновесным путем S₂ – S₁ > 0 dS > 0 S > 0		если U = const и V = const, то при равновесии S₂ – S₁ = 0 dS = 0 S = 0

Второе начало термодинамики. Самопроизвольные и несамопроизвольные процессы. Энтропия и энергия Гиббса как критерии равновесия и направления самопроизвольного процесса.

Существуют несколько эквивалентных формулировок второго начала термодинамики:

1.Постулат Клаузиуса: «Невозможен процесс, единственным результатом которого являлась бы передача тепла от более холодного тела к более горячему»[1] (такой процесс называется процессом Клаузиуса).

2.Постулат Томсона (Кельвина): «Невозможен круговой процесс, единственным результатом которого было бы производство работы за счет охлаждения теплового резервуара» (такой процесс называется процессом Томсона).

3.Другая формулировка второго начала термодинамики основывается на понятии энтропии:

«Энтропия изолированной системы не может уменьшаться» (закон неубывания энтропии).

Такая формулировка основывается на представлении об энтропии как о функции состояния системы, что также должно быть постулировано.

Самопроизвольные процессы – это неравновесные процессы, которые протекают без воздействия внешней силы в направлении достижения равновесия. Для проведения самопроизвольных процессов не только не затрачивается работа, но при соответствующих условиях эта система сама может произвести работу в количестве, пропорциональном происходящему изменению. Примерами самопроизвольных процессов могут служить переход тепла от более нагретого тела к менее нагретому, смешение газов, расширение газов в вакуум, превращение кинетической энергии движущегося тела в тепло и т.д. Все перечисленные процессы протекают в направлении, приближающем систему к равновесию.

Обратные по направлению процессы: переход тепла от холодного тела к горячему, разделение газовой смеси, сжатие газа и т.д. удаляют соответствующие системы от равновесия и без внешнего воздействия происходить не могут, т.е. для проведения таких процессов необходимо затратить работу в количестве, пропорциональном происходящим изменениям. Такие процессы называются несамопроизвольные.

Рассмотренные ранее равновесные процессы, при которых системы, бесконечно медленно изменяясь, проходят непрерывный ряд равновесных состояний, можно рассматривать в качестве промежуточных между процессами самопроизвольными и несамопроизвольными.

Термодинамическая система называется изолированной, если ее объем постоянен и она не обменивается с окружающей средой энергией и веществом.

Если обратиться к схеме, приведенной на рис. 1.15 (см. стр. 30), то для изолированной системы:
V₁ = V₂ = V = const U₁ = U₂ = U = const
Критерием самопроизвольного протекания процесса в изолированной системе является энтропия.
^ В изолированной системе могут самопроизвольно протекать только те процессы, которые приводят к возрастанию энтропии в системе. Когда энтропия достигнет максимального при данных U и V значения, все процессы прекратятся, и система достигнет равновесного состояния.

Итак,
если U = const и V = const, то при самопроизвольном процессе, протекающем неравновесным путем S₂ – S₁ > 0 dS > 0 S > 0		если U = const и V = const, то при равновесии S₂ – S₁ = 0 dS = 0 S = 0

В системе, не совершающей никакой работы, кроме работы расширения, и находящейся при постоянных температуре и давлении (Р = const, Т = const), самопроизвольно могут протекать только те процессы, которые приводят к уменьшению изобарно-изотермического потенциала системы (G). Когда G достигнет минимального значения при данных Р и Т, система приходит в равновесие и процесс прекращается.

Обозначим величины так, как на рис. 1.15 (см. стр. 30), тогда
если 1) A = PdV; 2) Р = const, Т = const, то при самопроизвольном процессе, протекающем неравновесным путем G₂ – G₁ < 0 dG < 0 G < 0		если 1) A = PdV; 2) Р = const, Т = const, то при равновесии G₂ – G₁ = 0 dG =0 G =0 $c:\documents and settings\admin\рабочий стол\физхим\b00001882-84.png$

Многие физические и химические процессы протекают при постоянном давлении и температуре, если они проводятся в открытых термостатированных реакторах. О направлении процессов и равновесии в таких системах судят по изменению изобарно-изотермического потенциала (свободной энергии) системы (G).

Объединенное уравнение I и II законов термодинамики. Энергия Гиббса и энергия Гельмгольца как критерии состояния равновесия и направления химического процесса.

1 2 3 4 5 6 7