Курсовая Теория электрической связи. Курсовая. Основы передачи и приёма дискретных сообщений

• Название: Основы передачи и приёма дискретных сообщений
• Анкор: Курсовая Теория электрической связи
• Дата: 24.05.2022
• Размер: 2.35 Mb.
• Имя файла: Курсовая.docx
• Тип: Курсовая; #547369
• страница: 2 из 3

3. Описание процесса принятия приёмником решения при приёме сигнала
Отношение правдоподобия для критерия минимума суммарной условной вероятности ошибки:

Λ= > (<) 1

Критерием идеального наблюдателя (Котельникова), согласно которому порог выбирается так, чтобы обеспечить минимум средней вероятности ошибки:

р_ош = р₀р₀₁+р₁р₁₀,

где р₀ - априорная вероятность гипотезы H₀ (сигнала нет),

р₁ - априорная вероятность гипотезы H₁ (сигнал есть).

Отношение правдоподобия для критерия идеального наблюдателя:

Λ= > (<)

Априорные вероятности гипотез - это вероятности присутствия в кодовой последовательности нулей и единиц соответственно [1].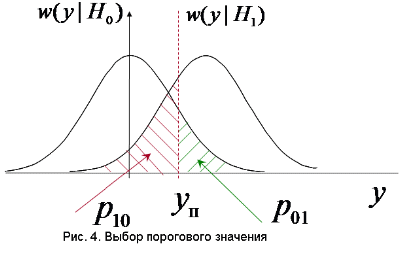



4. Расчёт характеристик системы согласно заданию №3

1. 
   Когерентный приём
   

Если в линии только шум с нулевым средним (гипотеза Н₀), то на выходе канала связи есть сигнал с Гауссовой плотностью распределения:

, [1/В]

Если в линии сумма сигнала и шума (гипотеза Н₁), то на выходе канала связи есть сигнал с Гауссовой плотностью распределения:

, [1/В]

Вычислим плотности распределения вероятностей мгновенных значений колебания на входе демодулятора при приёме посылки и паузы: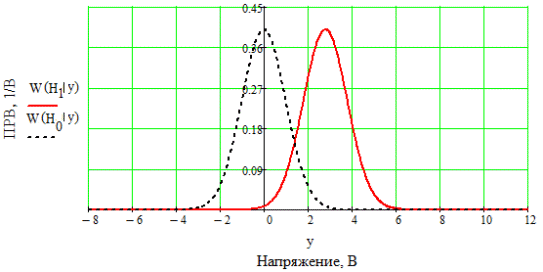



Рис.5. Плотности распределения вероятностей при когерентном приёме: сплошная линия - смесь сигнала и шума, пунктир - шум.

p₀=0,546

p₁=0,454

, [1/В]

, [1/В]

С помощью Mathcad найдём y_П: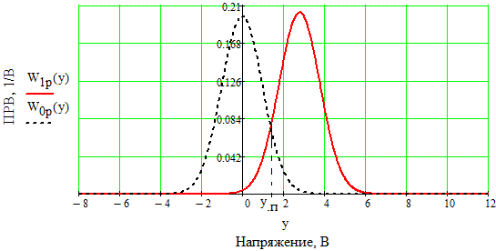



Рис.5. Выбор порогового значения y_П при когерентном приёме.



Т.е. y_П = 1.4 В

Определение условных вероятностей ошибок первого и второго рода и средней вероятности ошибки

Условная вероятность ошибки первого рода - ложной тревоги (передавалась единица, а принят - ноль):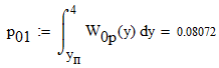



Условная вероятность ошибки второго рода - пропуск сигнала (передался ноль, а принята единица):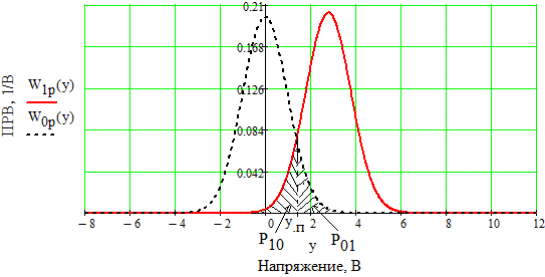


Рис. 6. Определение условных вероятностей ошибок первого и второго рода при когерентном приёме.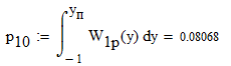



Таким образом, средняя вероятность ошибки:



где p₀₁ - вероятность «1» при передачи «0»; p₁₀ - вероятность «0» при передачи «1»

Определение скорости передачи информации при наличии помех



Для определения среднего количества передаваемой по каналу информации (приходящееся на один символ) I_kog нужно найду совместные вероятности всех сочетаний входных и выходных символов, а для этого запишу условные вероятности для входных символов при заданных входных.

p(1) = 0.454; p(0) = 0.546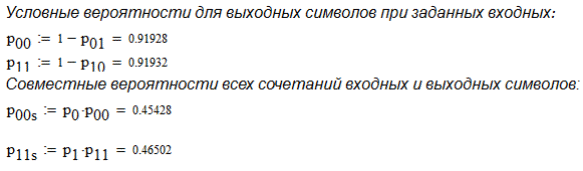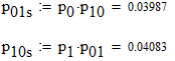



Безусловные вероятности выходных символов для нахождения энтропии источника:

p₁’= p(0)p_00s + p(1)p_10s = 0.475

p₀’ = 1 - p₁’ = 0.525

Энтропия источника:

Н_s = −р₁’∙log₂(р₁’) − р₀’ ∙log₂(р₀’)

Н_s = 0.993 бит

Энтропия источника, рассчитанная ранее: Н_k = 0.994 бит

Совместная энтропия входа и выхода канала: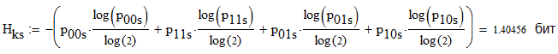



Среднее количество передаваемой информации по каналу:



Скорость передачи информации при наличии помех: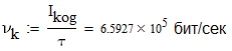





2) Некогерентный приём

Условная плотность распределения вероятностей шума:



Условная плотность распределения вероятностей суммы сигнала и шума:



где I₀(*) - модифицированная функция Бесселя первого рода нулевого порядка.

4.2.1.Определение оптимального порога при некогерентном приёме

Для определения оптимального по критерию идеального наблюдателя порога высчитаем условные плотности распределения вероятностей, умноженные на априорные вероятности гипотез H₀ и H_1.

p(1) = 0.454; p(0) = 0.546.

, [1/B]

, [1/B]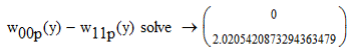



Таким образом, порог y_П = 2.02 (B)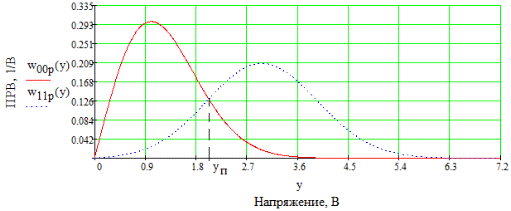



Рис. 7. Выбор порога при некогерентном приёме.

Определение условных вероятностей ошибок первого и второго рода и средней вероятности ошибки

Условная вероятность ошибки первого рода (ложная тревога):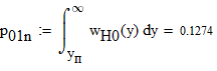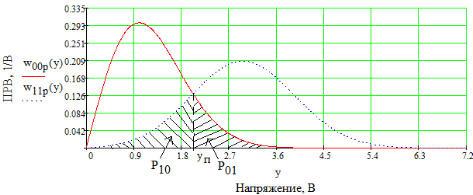





Рис.8. Определение условных вероятностей ошибок первого и второго рода при когерентном приёме.

Условная вероятность ошибки второго рода (пропуск сигнала):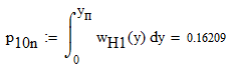



Таким образом, средняя вероятность ошибки:



Определение скорости передачи информации при некогерентном приёме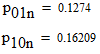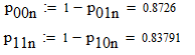





Совместные вероятности сочетаний входных и выходных символов:

p_0n = p(0)p_00n = 0.431

p_001n = p(0)p_01n = 0.063_1n = p(1)p_11n = 0.424_110n = p(1)p_10n = 0.082

Безусловные вероятности выходных символов для нахождения энтропии источника:

p_1n’= p(0)p_00n + p(1)p_10n = 0.513_0n’= 1 - p_1n’ = 0.487

Энтропия источника:

Н_sn = − p_1n’∙log₂(p_1n’) − p_0n’ ∙log₂(p_0n’) = 0.9995 бит

Энтропия источника, рассчитанная ранее: Н_k = 0.994 бит

Совместная энтропия входа и выхода цифрового канала:



Среднее количество передаваемой информации по каналу:



Скорость передачи информации при наличии помех:





Вывод:

При когерентном приёме сигнала вероятности ошибок первого и второго рода меньше, а значит и средняя вероятность ошибки меньше, чем при некогерентном. Скорость передачи информации выше при когерентном приёме. Потенциальная (наивысшая) помехоустойчивость реализуется в том случае, когда в точке приёма известны все параметры сигнала, т.е. форма, частота, задержка во времени и начальная фаза. Неизвестно только то, какой из возможных сигналов передаётся на данном интервале наблюдения. Поэтому когерентный приём лучше, чем некогерентный. Но на практике обеспечить когерентный прием не всегда удаётся, так как один или несколько параметров принимаемого сигнала оказываются неизвестными.

5. 
   Расчёт согласованного фильтра
   

В случае приёма сигнала известной формы демодулятор должен вычислить значение корреляционного интеграла, которое сравнивается с порогом, выбираемым в соответствии с принятым критерием эффективности.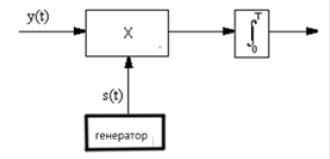



Рис 9. Структура коррелятора.

Коррелятор является нестационарным (параметрическим) устройством и включает генератор опорного колебания, совпадающего по форме с ожидаемым сигналом на интервале наблюдения, и интегратор, на выходе которого в момент окончания интервала наблюдения формируется значение, сравниваемое с порогом.

На вход фильтра поступает смесь гауссова шума с заданной дисперсией γ² и радиоимпульса с известными огибающей, длительностью, частотой заполнения и начальной фазой.

s(t) = Acos(γ₀t+φ₀)

Этот фильтр, описывается импульсной характеристикой h_сф(t), при этом выходной сигнал определяется свёрткой (интегралом Дюамеля), которая для момента t₀ сравнения с порогом равна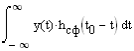

А с учётом финитности посылки: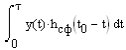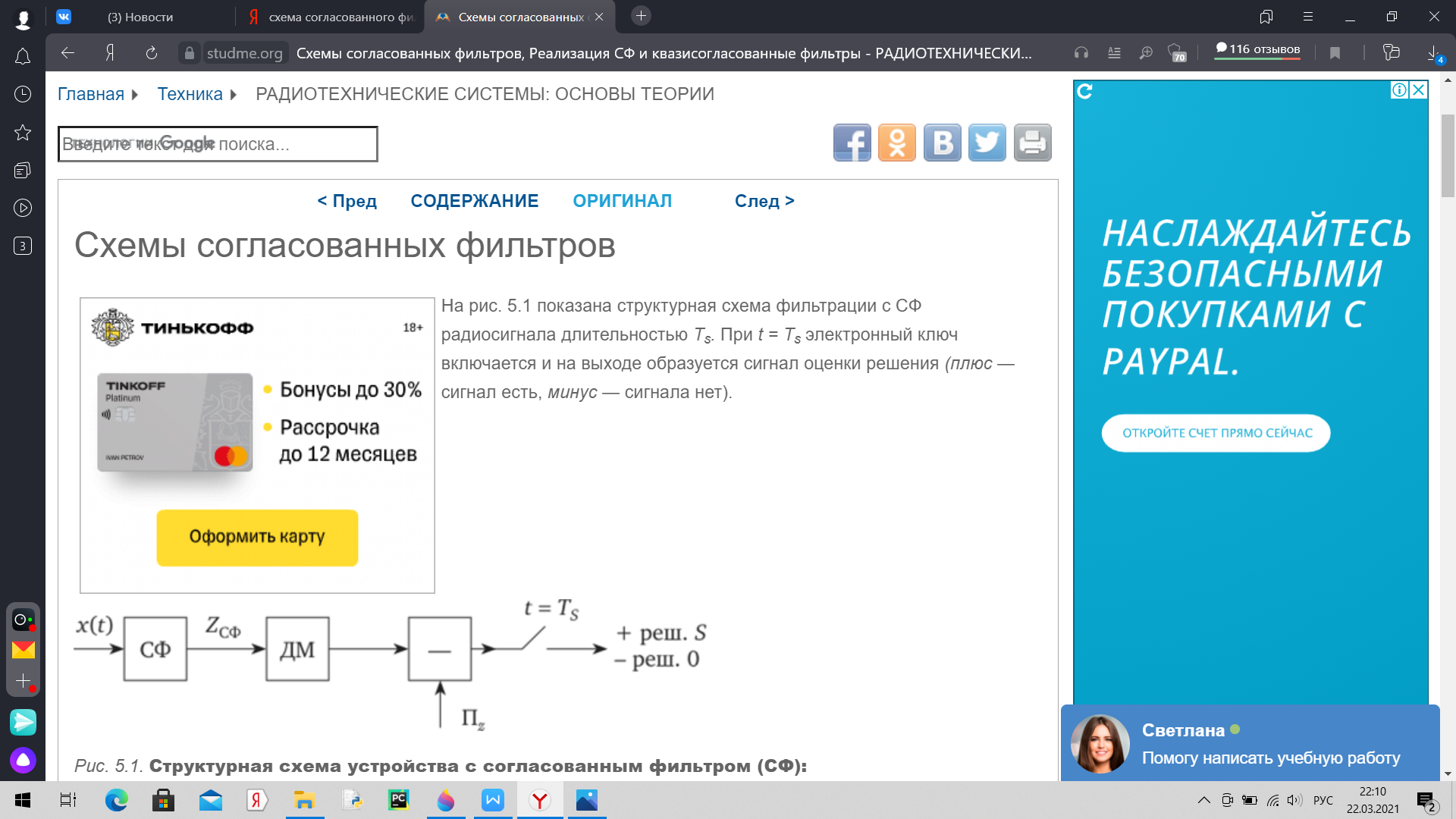





Рис 10. Структурная схема фильтрации с СФ.

Структурная схема фильтрации с СФ радиосигнала длительностью Ts. При t = Ts электронный ключ включается и на выходе образуется сигнал оценки решения (плюс — сигнал есть, минус — сигнала нет).

Учитывая, что в момент t₀ на выходе согласованного фильтра должно быть выработано значение корреляционного интеграла, приходим к выводу, что должно выполняться равенство:



где

Исходя из этого, можно сделать вывод, что:



где s(t) - посылка (прямоугольный радиоимпульс)

Таким образом, импульсная характеристика согласованного фильтра совпадает по форме с ожидаемым сигналом, обращённым во времени и задержанным на время t₀. Для выполнения требования каузальности необходимо, чтобы t₀ было не меньше, чем τ.

Зная импульсную характеристику фильтра можно найти КЧХ согласованного фильтра:



где S(ω) - спектральная плотность посылки [3].

Таким образом:



Можно видеть, что АЧХ совпадает по форме с модулем спектральной плотности сигнала. Следовательно, фильтр подчеркивает сильные и подавляет слабые частотные компоненты сигнала.



ФЧХ состоит из двух слагаемых. Первое обеспечивает суммирование всех частотных компонент сигнала «в фазе», благодаря чему в момент времени t₀, обусловленный множителем e^-jwt_0, имеет место максимальное значение отклика, численно равное энергии сигнала [3].

Действие согласованного фильтра на аддитивную смесь сигнала с шумом можно рассматривать по отдельности в силу линейности фильтра.

Сигнальная составляющая выходного процесса:



Шумовая составляющая: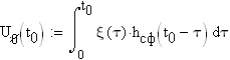



Дисперсию шума на выходе можно найти следующим образом: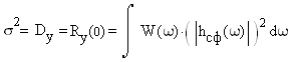



W(ω) - спектральная плотность мощности шума.

Отношение сигнал/шум (ОСШ) по мощности на выходе СФ будет максимальным при условии t₀ = τ. Оно равно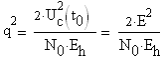



Принимая ψ=1, имеем Е_h = E, тогда:



Выигрыш в отношении сигнал/шум по сравнению со случаем однократного отсчёта равен: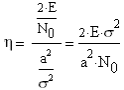



Учитывая, что шум на входе согласованного фильтра квазибелый с полосой (-F, F), содержащей 99% энергии сигнала, ²df = 0.99 ²df = 0.99E, получим F=10.286/τ, тогда СПМ шума N₀/2 = σ²/(2F).