Курсовая Теория электрической связи. Курсовая. Основы передачи и приёма дискретных сообщений

• Название: Основы передачи и приёма дискретных сообщений
• Анкор: Курсовая Теория электрической связи
• Дата: 24.05.2022
• Размер: 2.35 Mb.
• Имя файла: Курсовая.docx
• Тип: Курсовая; #547369
• страница: 1 из 3

МОСКОВСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ ГРАЖДАНСКОЙ АВИАЦИИ

Кафедра «Основ радиотехники и защиты информации»

КУРСОВАЯ РАБОТА

По дисциплине: «Теория электрической связи»

На тему: «Основы передачи и приёма дискретных сообщений»


Работу выполнил:

студент группы БИ 3-1

Краснобабцев И.Ф.

Проверил: профессор Емельянов В.Е.

Москва 2022

Вариант 1А

Содержание

Введение...................................................................................................................5

Структурная схема системы связи согласно пункту 2.1......................................6 Описание принципов кодирования источника при передаче дискретных сообщений. Построение кода. Кодирование построенным кодом произвольной фразы................................................................................................6

Расчет характеристик системы согласно пункту 2.2..........................................10

Описание процесса принятия приемником решения при приеме сигнала....................................................................................................................12 Расчет характеристик согласно пункту 2.3.........................................................13

Описание принципов корреляционной обработки и согласованной фильтрации; расчет согласованного фильтра и его принципиальную схему.......................................................................................................................19

Расчет характеристик согласно пункту 2.4.........................................................22

Структурная схема системы связи согласно пункту 2.5....................................27

Описание принципов помехоустойчивого кодирования при передаче дискретных сообщений. Построение (7,4)-кода Хемминга. Расчет характеристик согласно пункту 2.5......................................................................28

Описание процессов декодирования последовательности, содержащей двукратную ошибку, согласно пункту 2.6...........................................................32 Заключение.............................................................................................................34

Список использованной литературы...................................................................35


Задание и исходные данные к тематике группы 2А

2А.2. Задание

2.1 Составить обобщённую структурную схему системы связи для передачи дискретных сообщений, содержащую кодер источника, модулятор, канал связи, демодулятор и декодер. Изобразить качественно временные диаграммы сообщений и сигналов в промежуточных точках структурной схемы. Все диаграммы должны сопровождаться краткими описаниями.

2.2 Определить энтропию и избыточность источника, выполнить кодирование источника (построить экономный код), рассчитать энтропию и избыточность кода, вероятности двоичных символов, передаваемых по каналу, среднюю длину кодового слова, скорость передачи информации по каналу без помех.

2.3 Рассмотреть случаи когерентного и некогерентного приёма путём взятия однократного отсчёта смеси высокочастотного сигнала с шумом на выходе линии связи и процесса на выходе детектора огибающей. Определить оптимальный по критерию идеального наблюдателя порог для принятия решения о принимаемом символе при когерентном и некогерентном приёме, условные вероятности ошибок первого и второго рода, среднюю вероятность ошибки, скорость передачи информации при наличии помех. Сделать выводы по результатам расчётов.

2.4 Определить импульсную и комплексную частотную характеристики согласованного фильтра для приёма посылки. Определить условные вероятности ошибок и среднюю вероятность ошибки при когерентном приёме с использованием согласованного фильтра. Оценить выигрыш в отношении сигнал/шум за счёт согласованной фильтрации.

2.5 Составить обобщённую структурную схему системы связи для передачи дискретных сообщений, использующую, кроме статистического, также помехоустойчивое (канальное) кодирование. Опираясь на результаты пунктов 2.3 и 2.4, рассчитать вероятности однократной и двукратной ошибок в пределах одного кодового слова и охарактеризовать способность кода к обнаружению и исправлению ошибок.

2.6 Внести в кодовую последовательность на выходе демодулятора двукратную ошибку в пределах одной кодовой комбинации. Выполнить процедуру декодирования полученной последовательности в соответствии с кодом Хэмминга, а затем произвести декодирование статистического кода. Оценить результат, сделать выводы.

2А.1. Исходные данные

1. 
   Алфавит источника сообщений с априорными вероятностями символов согласно варианту ( табл. 2.1).
   
2. 
   Код для сокращения избыточности (сжатия) определяется подвариантом (табл. 2.2) – код Шеннона-Фано (ШФ) или код Хоффмена (Хф).
   
3. 
   Канальное кодирование выполняется (7,4)-кодом Хэмминга.
   
4. 
   Вид модуляции – амплитудная телеграфия (АТ) с пассивной паузой.
   
5. 
   Форма посылки – прямоугольный радиоимпульс.
   
6. 
   Амплитуда сигнала на входе демодулятора , длительность посылки τ , дисперсия шума на входе демодулятора определяются подвариантом (табл. 2.2).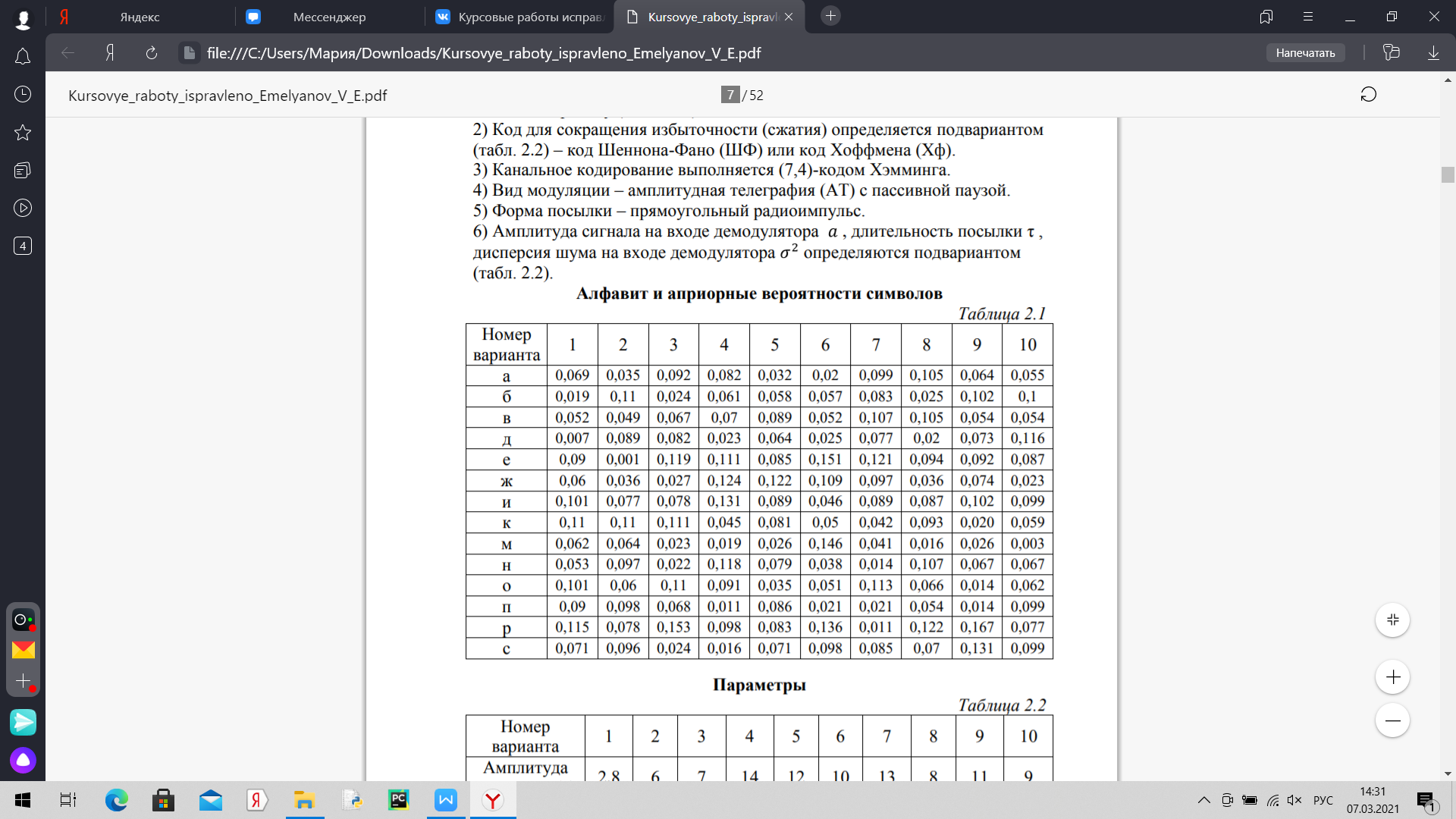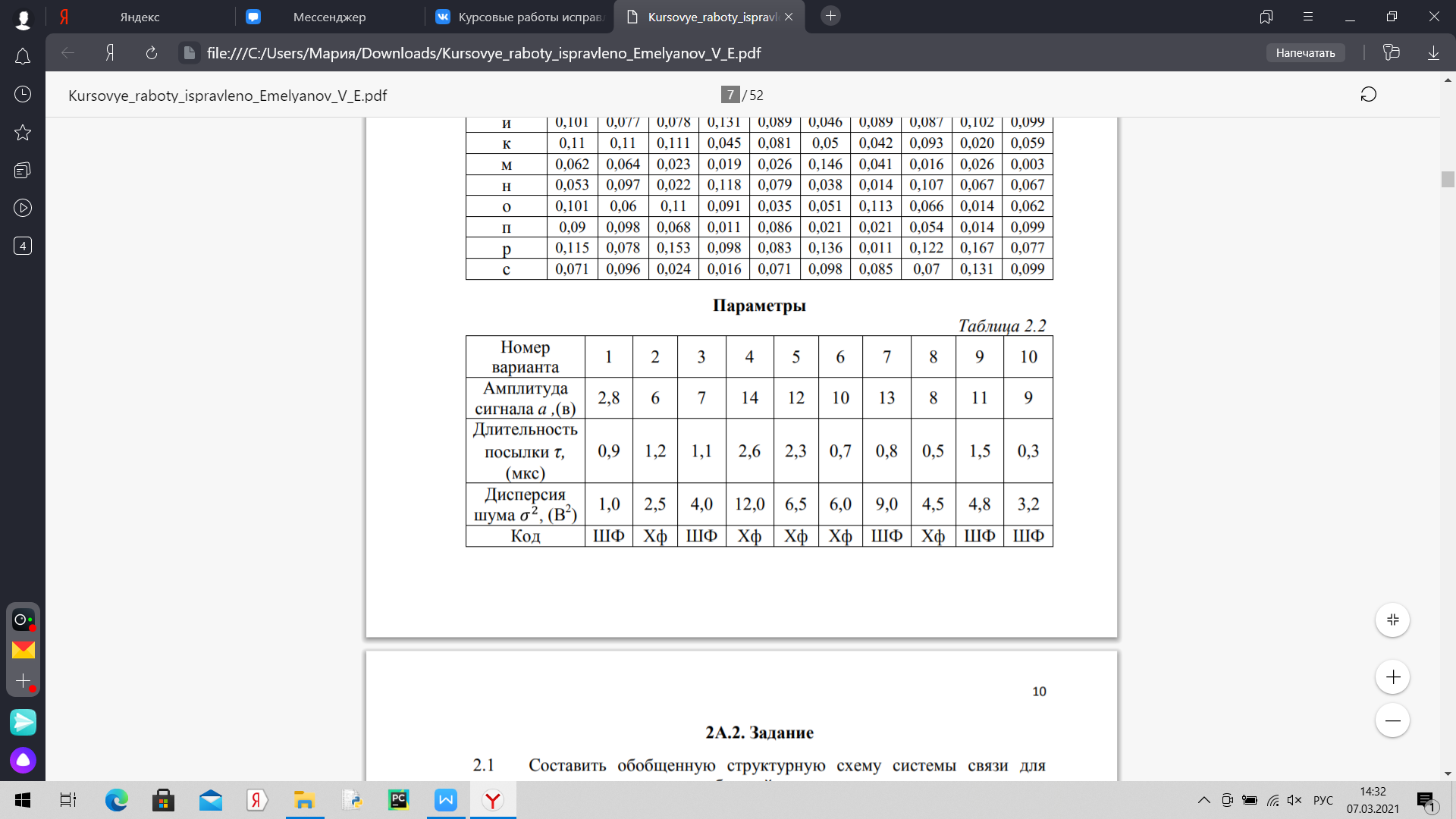
   

Введение

В современном мире в области электросвязи всё более широко используются цифровые виды информации. Это объясняется тем, что цифровые системы передачи имеют такие преимущества как высокая помехоустойчивость, слабая зависимость качества передачи от длины линии связи, стабильность электрических параметров каналов связи, эффективность использования пропускной способности при передаче дискретных сообщений и др.

Целью данной курсовой работы является разработка системы связи для передачи дискретных сообщений. Дискретные сигналы возникают в тех случаях, когда источник сообщений выдает информацию в фиксированные моменты времени. Такие сигналы приобрели особое значение в последние десятилетия под влиянием совершенствования техники связи и развития способов обработки информации быстродействующими вычислительными устройствами. Из-за наличия в канале связи помех, прием сообщений становится ненадежным, и мы можем получить неверную (ложную) информацию. Поэтому, например, вопрос помехоустойчивости является одним из важнейших вопросов электрической связи.

В данной курсовой работе изучаются методы кодирования сообщения с целью сокращения объёма алфавита символов и достижения повышения скорости передачи информации. Предполагается использование двоичных кодов, как для статистического, так и для помехоустойчивого кодирования. Затем производится декодирование - восстановление символов исходного алфавита, в результате чего должен быть воспроизведён переданный текст.
Структурная схема системы связи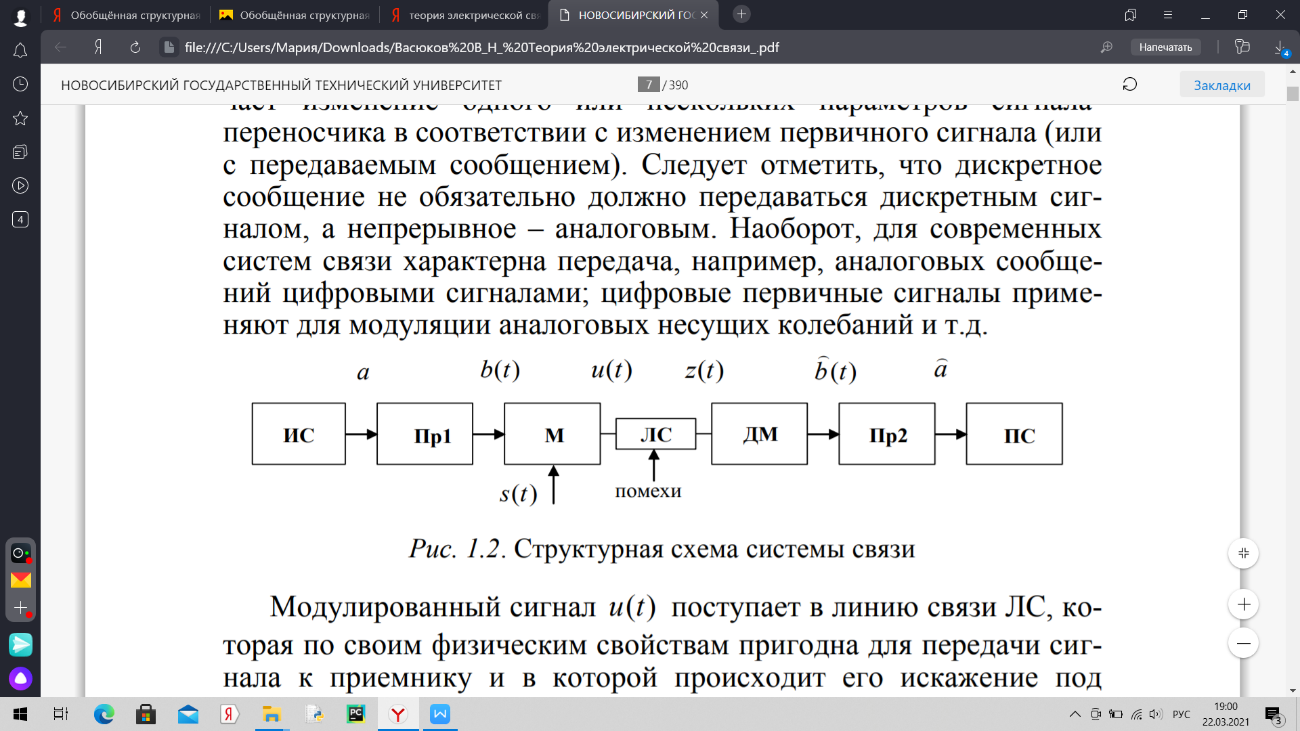



Рис. 1. Обобщённая структурная схема системы связи [2]

Модулированный сигнал u(t) поступает в линию связи ЛС, которая по своим физическим свойствам пригодна для передачи сигнала к приемнику и в которой происходит его искажение под влиянием характеристик линии, а также неизбежное воздействие на сигнал вредных колебаний (помех). Вследствие этого колебание z(t) , поступающее с выхода линии связи ЛС на демодулятор ДМ, отличается от переданного сигнала u(t) , поэтому вырабатываемый демодулятором сигнал b(t) в общем случае отличается от первичного сигнала b(t). Качество демодулятора (и системы в целом) тем выше, чем меньше это отличие. Сигнал b(t) преобразуется преобразователем Пр2 в сообщение a , передаваемое получателю сообщения ПС [2].

1. 
   Построение кода
   

Кодирование источника по методу Шеннона - Фано.

Принцип построения кода Шеннона - Фано состоит в упорядочении всех символов алфавита (в нашем случае букв) по убыванию вероятностей. Затем все буквы делятся на две (неравные в общем случае) группы так, что сумма вероятностей букв для обеих групп одинакова или примерно одинакова, и в качестве первого символа кодового слова каждой букве первой группы присваивается кодовый символ 0, а каждой букве второй группы - символ 1 (или наоборот). Далее первая и вторая группы делятся на подгруппы в соответствии с принципом равной вероятности, и эта процедура продолжается до тех пор, пока алфавит источника не будет исчерпан.

Необходимо обратить внимание на следующее свойство полученного кода: ни одна кодовая комбинация не является началом какой-либо другой кодовой комбинации (префиксное правило). Такие коды называются неперекрываемыми (неприводимыми) [1].

Закодируем заданный алфавит методом Шеннона - Фано.
Таблица 3

Алфавит источника	Вероятность символа	Комбинация кодовых символов					Длина к.с.	Число единиц
αk	p(αk)	1	2	3	4	5	Mk
и	0.101	0	0	0			3		0
ж	0.06	0	0	1			3		1
н	0.053	0	1	0	0		4		1
е	0.09	0	1	0	1		4		2
р	0.115	0	1	1			3		2
о	0.101	1	0	0			3		1
а	0.069	1	0	1	0		4		2
в	0.052	1	0	1	1		4		3
б	0.019	1	1	0	0		4		2
к	0.11	1	1	0	1		4		3
д	0.023	1	1	1	0	0	5		3
м	0.062	1	1	1	0	1	5		4
с	0.071	1	1	1	1	0	5		4
м	0.011	1	1	1	1	1	5		5

Закодируем сообщение: Краснобабцев Илья. Отсутствующие в алфавите источника буквы пропускаются:. Краснобабев И

Получившийся код: 1101 011 1010 11110 0100 100 1100 1010 1100 0101 1011 000
Первым двум буквам сообщения соответствует код: 1101011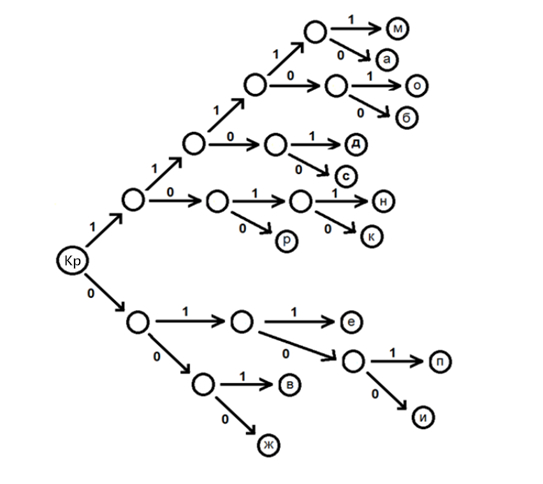



Рис.2 Дерево кодирования кода Шеннона-Фано

Изобразим качественные временные диаграммы сигналов во всех промежуточных точках структурной схемы (рис.3). Возьмём фрагмент сигнала, отвечающего двум первым буквам сообщения «к» - 1101 и «р» - 011.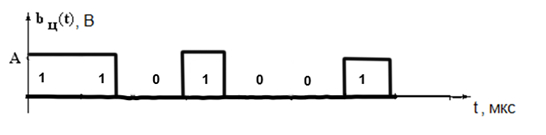



Рис. 3 а) Фрагмент сигнала на входе модулятора.
На вход модулятора поступает последовательность кодовых символов в виде прямоугольных радиоимпульсов. Наличие импульса - «1», его отсутствие - «0».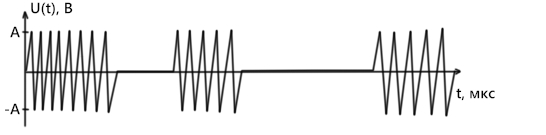



Рис. 3. б) Фрагмент синала на выходе модулятора

Последовательность импульсов непригодна для передачи по линии связи, поэтому она поступает на модулятор, где используется для модуляции другого колебания s(t) - переносчика. Вид модуляции - амплитудная телеграфия с пассивной паузой. Модулированное колебание U(t) поступает в линию связи.

В линии связи сигнал взаимодействует с помехой, поэтому на вход демодулятора поступает их сумма. Также сигнал в линии связи подвергается искажениям, но мы в данном случае пренебрегаем этим условием.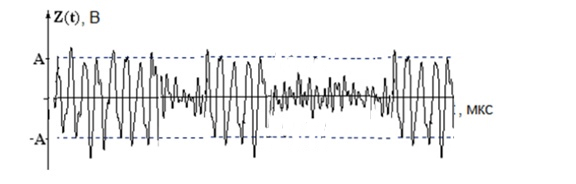



Рис. 3. в) Фрагмент сигнала на входе модулятора
Таким образом, на входе демодулятора присутствуют случайные колебания двух видов - реализация шума или сумма детерминированного сигнала и шума, что соответствует двум гипотезам.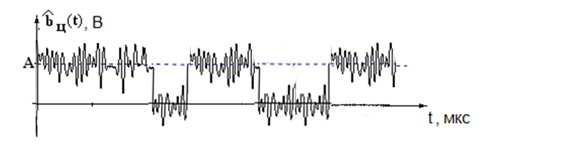



Рис. 3. г) Фрагмент сигнала на выходе демодулятора.

Задача демодулятора - принять на основе наблюдения решение о том, какая именно гипотеза выполняется на данном интервале, и на основании этого сформировать последовательность двоичных символов, которая затем подвергается декодированию. Эта последовательность может отличаться от исходной b_ц(t). Для уменьшения вероятности ошибки мы и будем использовать кодирование [3].


2. Расчёт характеристик системы согласно заданию №2

Рассматривая источник без памяти, запишем энтропию дискретного источника А в виде:

,

где K - количество символов в алфавите, p(α_k) - вероятность k-того символа.
Рассчитаем энтропию источника:
=

=

= 3.526 (бит)

Следовательно, энтропия источника: H (A) = 3,526 бит.

Максимальная энтропия для данного источника:
бит.
Найдём избыточность источника:

Средняя длина кодовой комбинации:



Для построенного кода средняя длина кодовой комбинации:

µср= 3 * (0,131 + 0,124 + 0,098 + 0,091) + 4 * (0,118 + 0,111 + 0,082 + 0,07 + 0,061 + 0,045) + 5 * (0,023 + 0,019 + 0,016 + 0,011) = 3,625 (символов)

Согласно теореме Шеннона при оптимальном кодировании можно достичь средней длины:

μ_min=H(A)/log₂2= H(A)=3.526 (символа)

То есть, μ_ср≠μ_min. Таким образом, построенный код не является оптимальным, потому что на каждом шаге процедуры построения кода не удавалось разделить символы на группы с равными вероятностями.

Расчёт энтропии, избыточности кода, вероятности двоичных символов, передаваемых по каналу, скорость передачи информации:

Определим вероятность появления определённого символа в кодовой комбинации (пусть это будет символ 1): p(1) = (0,131 * 0 + 0,124 * 1 + 0,118 * 1 + 0,111 * 2 + 0,098 * 2 + 0,091 * 1 + 0,082 * 2 + 0,07 * 3 + 0,061 * 2 + 0,045 * 3 + 0,023 * 3 + 0,019 * 4 + 0,016 * 4 + 0,011 * 5) / 3,625 = 0,454

В таком случае, вероятность появления символа 0:

p(0) = 1- 0,454 = 0,546 - априорная вероятность 0.

Определим энтропию кода :

Т.к. алфавит кода состоит из двух символов 0 и 1, поэтому энтропия кода равна:

= - (0,546 * log 2 0,546 + 0,454 * log 2 0,454) = 0,994

Рассчитаем избыточность кода:



Только будем учитывать, что при передаче бинарного кода, его максимальная энтропия: Н_{к мах}=1
Скорость передачи информации по каналу без помех:

, где τ - длительность посылки.

Поскольку Н_К =0.994 (бит) и τ = 2.6 (мкс), получаем:

I = 0,994 / (2,6 * 10ˉ⁶) = 0,382 * 10⁶ бит/сек.

или

I = H(A) / (µ * τ) = 3,526 / (3,625 * 2,6 * 10ˉ⁶) = 0,374 * 10⁶ бит/сек.