Курсовая Теория электрической связи. Курсовая. Основы передачи и приёма дискретных сообщений
 Скачать 2.35 Mb. Скачать 2.35 Mb.
|
|
6. Расчёт характеристик системы согласно заданию № 4 Определение импульсной характеристики согласованного фильтра для приёма посылки Рассмотрим фильтр для принятия элементарной посылки. На вход фильтра поступает смесь гауссова шума, с заданной дисперсией σ2, и радиоимпульса, с известными огибающей, длительностью, частотой заполнения и начальной фазой (когерентный приём). Для нашего радиоимпульса: 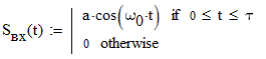 где a - амплитуда, τ - длительность, ω0 - частота заполнения. Заполнение высокочастотное, примем ω0= 2*π*5 MГц. 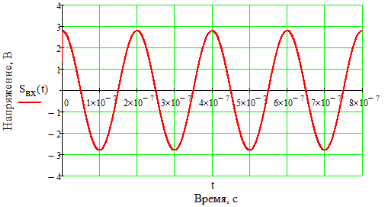 Рис. 10. Сигнал на входе согласованного фильтра. Тогда импульсная характеристика такого фильтра будет представлять собой зеркальное отображение временной функции сигнала, задержанное на время, не менее длительности сигнала. где t0 - величина не меньше τ. 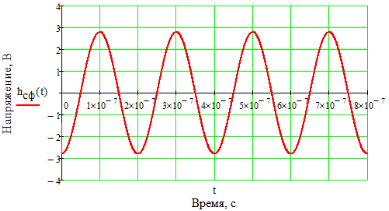 Рис.11. Импульсная характеристика согласованного фильтра. Для нахождения КЧХ фильтра необходимо определить спектральную плотность посылки. Используем прямое преобразование Фурье и теорему сдвига: 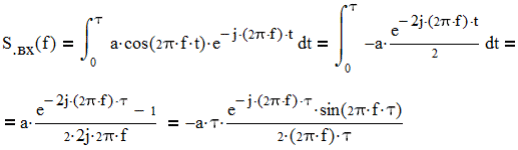 Комплексно-частотная характеристика согласованного фильтра: Амплитудно-частотная характеристика: 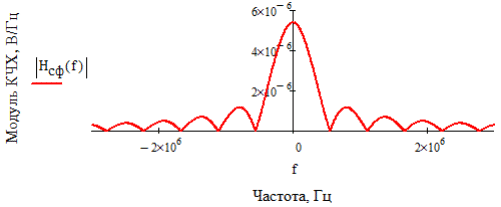 Рис. 12. АЧХ согласованного фильтра Отклик согласованного фильтра на посылку Отклик согласованного фильтра на посылку будет определяться сверткой: 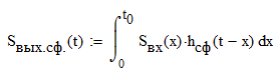 Отклик фильтра будет по форме отличаться от исходного сигнала. Дело в том, что от фильтра не требуется передать форму сигнала, а нужно создать максимальный всплеск в момент времени t0. Можно видеть, что при t=t0=9*10-7 значение отклика максимально и численно равно энергии сигнала. 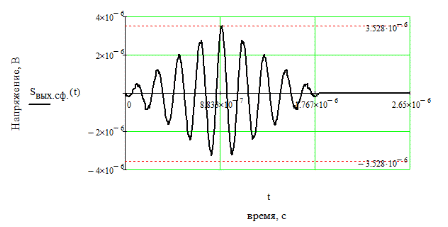 Рис. 12. Сигнал, полученный на выходе согласованного фильтра. Это можно объяснит тем, что отклик представляет собой АКФ посылки, которая достигает максимума, равного энергии сигнала, при нулевом значении аргумента. 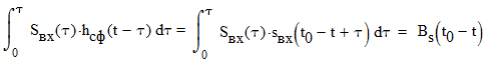 3) Определение условных вероятностей ошибки и средней вероятности ошибки Для определения условных вероятностей ошибки и средней вероятности ошибки при когерентном приёме с использованием согласованного фильтра необходимо найти дисперсию шума на выходе и рассмотреть гауссовы плотности распределения вероятностей. Мы можем найти дисперсию по формуле: 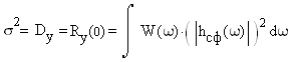 О помехе нам известно, что это квазибелый шум с нулевым средним, а значит имеет следующую СПМ: 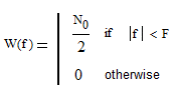 Учитывая, что в данной полосе частот содержится 99% энергии сигнала, найдём F: 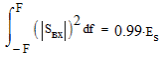 Решая данное уравнение, получим: F = 11.4*106 Гц - полоса частот, в которой сосредоточена мощность шума. Найдём N0: N0 = 1/(11.4*106) = 8.75*10-8 В2/Гц. Теперь можем найти СКО на выходе согласованного фильтра: 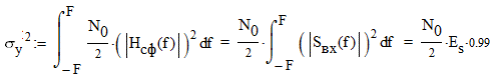 Зная СКО на выходе, мы можем определить и построить ПРВ на выходе согласованного фильтра:  Постоим график и найдём порог согласно критерию идеального наблюдателя: 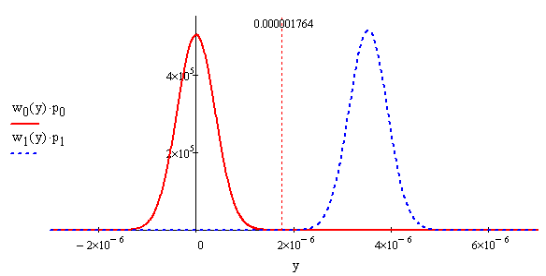 Рис. 13. График ПРВ на выходе согласованного фильтра. В данном случае порог равен уп = 0.000001764 В. Зная порог, определим условные вероятности ошибок: 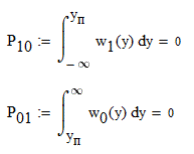 Найдём среднюю вероятность ошибки: Для наглядности сравним полученные средние вероятности ошибки: Таблица 8.1
Можно сделать вывод о том, что использование согласованного фильтра значительно уменьшает среднюю вероятность ошибки. 4) Определение выигрыша в отношении сигнал\шум за счет согласованной фильтрации Для начала определим отношение сигнал\шум по напряжению и по мощности на входе согласованного фильтра: 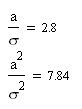 Отношения сигнал\шум по напряжению и по мощности на выходе согласованного фильтра: 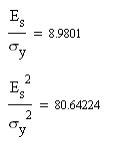 Выигрыш в ОСШ напряжению и по мощности составит: 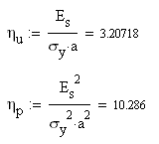 7. Структурная схема связи согласно пункту 2.5 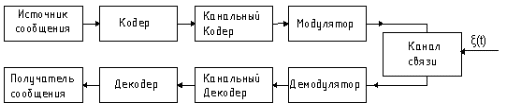 Рис.14. Структурная схема системы связи для передачи дискретных сообщений при помехоустойчивом кодировании. Декодирование осуществляется в следующем порядке: вначале производится декодирование помехоустойчивого кода, а затем на основе полученной двоичной последовательности производится восстановление символов исходного алфавита. 8. Описание принципов помехоустойчивого кодирования при передаче дискретных сообщений. Построение - кода Хемминга Код порождается матрицей кодирования (порождающей матрицей):  Кодовые слова имеют структуру: С = ( х1, х2, х3, х4, с5, с6, с7 ), где с5 = х1 + х2 + х3 с6 = х2 + х3 + х4 с7 = х1 + х2 + х4 (подразумевается сложение по модулю 2). Реализовать такое кодирование можно при помощи следующего устройства: 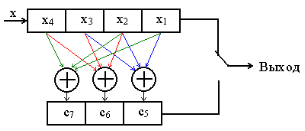 Рис. 15. Структура кодера для систематического (7,4) - кода. Для обнаружения ошибок может использоваться порождающая матрица Н:  Умножая по модулю 2 слева вектор-строку, соответствующую принятой комбинации, на транспонированную матрицу НТ, получаем вектор - синдром σ. Если σ - нулевой вектор, то в этом случае символ передался без ошибки, если же σ - вектор, совпадающий с одним из столбцов проверочной матрицы, то в этом случае в символе, номер которого соответствует номеру этого столбца, произошла ошибка. 1) Построение - кода Хемминга Исходная фраза: «Корякина Мария». При этом отсутствующие буквы в алфавите пропускались. Код этой фразы: 1101 100 011 1101 000 0100 1010 11111 1010 011 000 Разобьём этот код на блоки по 4 символа и недостающие дополним нулями: 1101.1000.1111.0100.0010.0101.0111.1110.1001.1000 Эти блоки представим в виде матрицы информационных (разрешённых) символов:  Запишем порождающую матрицу G: 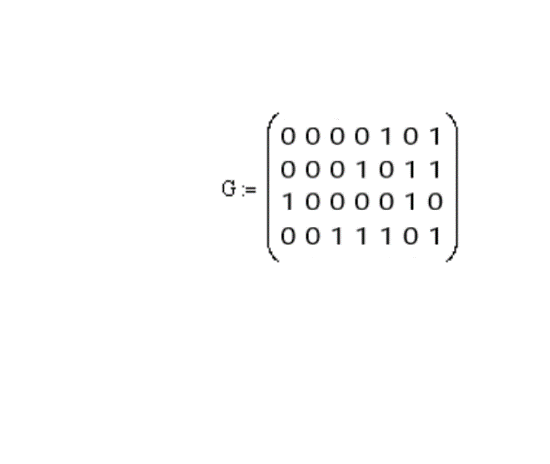 Каждая строка матрицы С равна до четвёртого символа соответствующему столбцу матрицы Х. Последующие три символа в каждой строке матрицы С и есть контрольные символы: С5, С6, С7 соответственно, где С5=x1+x2+x3; C6=x2+x3+x4; С7=x1+x2+x4. Тогда матрица кодирования:  Каждая строка в матрице С будет являться кодовым символом. Составленная в коде Хемминга фраза будет выглядеть так: 1101001.1000101.1111111.0100111.0010110.0101100.0111010.1110100.1001110.1000101. Или матрицу кодирования можно найти с помощью порождающей матрицы: В результате получаем: 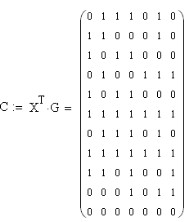 2) Расчёт вероятностей однократной и двукратной ошибок в пределах одного кодового слова Расчёт вероятностей однократной и двукратной ошибок в пределах одной кодовой комбинации длины n можно выполнить по формуле биномиального распределения вероятностей: P(k)=Cnkpk(1-p)n-k, где k следует положить равным соответственно 1 и 2. В качестве p подставим среднюю вероятность ошибки при приеме одного символа рош = 0.0807. Вероятность однократной ошибки: 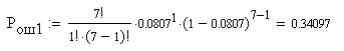 Вероятность двукратной ошибки: 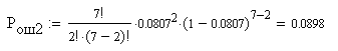 Итак, вероятности ошибок малы. Охарактеризуем способность кода к выявлению и исправлению ошибок. Предположим что передавалась разрешённая комбинация 0110001, и при передаче произошла: А) однократная ошибка 1110001 Б) двукратная ошибка 1110000 Проверить наличие ошибки можно с помощью проверочной матрицы Н:  Если при умножении вектора-строки на транспонированную матрицу в результате получится вектор (синдром) являющийся нулевым, то ошибки нет. В противном случае присутствуют ошибки.  Можно видеть, что наличие ошибок было определено в обоих случаях. Однако в случае однократной ошибки ошибочный 1-й символ, как ошибочный, был определен верно, что дает возможность его исправить, а в случае двукратной ошибки синдром указывает на ошибку в 5-м символе, и подобное решение не является верным. Из полученных результатов можно сделать вывод, что код Хемминга (7,4) обнаруживает однократные и двукратные ошибки, но исправляет только однократные.  9. Описание процессов декодирования последовательности, содержащей двукратную ошибку, согласно пункту 2.6 Внесем в кодовую последовательность на выходе демодулятора двукратную ошибку в пределах одной кодовой комбинации. Пусть матрица Сu - c введенной двукратной ошибкой. 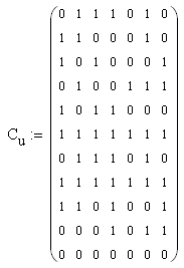 Определим местонахождение двукратной ошибки. Из результатов на следующей странице можно сделать вывод, что ошибка допущена в кодовом слове, третьем элементе. Декодер может исправить ошибку, прибавив (по модулю 2) к ошибочному символу единицу. 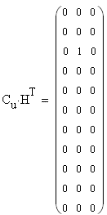 Выполним процедуру декодирования полученной последовательности в соответствии с кодом Хемминга. Отметим, что кодовые слова (строки матрицы Су) имеют следующую структуру: В кодовых словах k первых символа повторяют символы информационного вектора, а остальные (n-k) символов формируются из информационных и являются проверочными: Нетрудно видеть, что для 3-ой строки данные условия не выполняются, это свидетельствует о наличии ошибки. Декодирование может заключаться в отбрасывании проверочных символов, но это не обеспечит обнаружения и исправления ошибок. Произведем подобную процедуру: 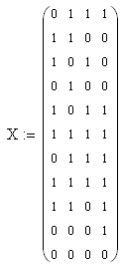 Зная свойство кода о том что ни одна кодовая комбинация не является началом какой-либо другой кодовой комбинации, произведем декодирование статистического кода (полученное сообщение сравним с исходным): Исходный код: 1101 100 011 1101 000 0100 1010 11111 1010 011 000 Получившийся код: 1111 100 011 1101 000 0100 1010 11111 1010 011 000 Из полученных результатов видно, что ошибки в пределах одной кодовой последовательности исказили часть сообщения, и это привело к выбору ошибочных символов. Заключение В данной работе рассмотрена простейшая модель системы передачи информации, которая может быть распространена на любую реальную систему передачи дискретных сообщений. В дальнейшем, при разработке более сложных систем связи, возможно использование результатов данной работы. После проведения расчетов можно убедиться в следующих известных фактах: 1. Когерентный прием обладает рядом преимуществ перед некогерентным (более высокая скорость передачи информации, сравнительно малая вероятность средней ошибки). Для данных способов приема сигнала результаты, полученные при расчете, вполне справедливы, т.к. при когерентном приеме известна форма сигнала, частота заполнения и начальная фаза, а значит, и вероятность ошибиться меньше, чем при некогерентном приеме, когда нам известна лишь форма огибающей сигнала. 2. Согласованная фильтрация применяется для повышения отношения сигнал/шум на выходе сигнала. Это, в свою очередь, увеличивает помехоустойчивость системы (вероятность безошибочного решения). Иными словами, согласованный фильтр нужен для наиболее надежного принятия решения о наличии или отсутствии сигнала на входе приемника. 3. (7,4)-код Хемминга обнаруживает одно- и двукратные ошибки и исправляет однократные, но в тоже время он увеличивает избыточность кода, следовательно, уменьшает скорость передачи информации. В случае если кодовое слово с ошибкой будет схоже с другой разрешенной комбинацией (кодовым словом), ошибки обнаружено не будет. Код Хемминга также увеличивает избыточность, что уменьшает скорость передачи информации. В ходе данной работы были использованы основные принципы кодирования и передачи информации. Список использованной литературы: Теория электрической связи. Пособие по выполнению курсовой работы, МГТУ ГА, Москва-2015. В. Е. Емельянов Теория электрической связи. Учебники НГТУ / Новосибирск: изд-во НГТУ, 2005. Васюков В.Н. Баскаков С.И. Радиотехнические цепи и сигналы: - М.: Высш. шк., 2003. |
