ОСНОВЫ работы в MathCad. Основы работы в математическом пакете Mathcad
 Скачать 8.94 Mb. Скачать 8.94 Mb.
|
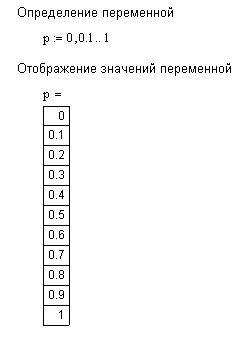
5.10. Определение переменных, принимающих значения из заданного промежуткаВ системе MathCAD предоставлена возможность определения переменных, принимающих значения из заданного промежутка, причем соседние значения удалены на равные расстояния друг от друга. При этом задается только начальное значение, следующее значение (второе значение, неявно задающее шаг изменения значения переменной) и конечное значение. Строго говоря, переменные, принимающие значения из промежутка, представляют собой векторы с равноудаленными значениями компонент. В качестве переменных, принимающих значения из промежутка, можно использовать только идентификаторы без индексов. Формат определения переменной: Имя_переменной := начальное_значение,начальное_значение + шаг .. конечное_значение Заметим, что при наборе знак «:=» проявляется после набора «:» , а знак «..» проявляется после набора «;». Если конечное значение при данном значении шага не достигается точно, последним значением переменной будет наибольшее значение из заданного промежутка, не превышающее конечное значение. Кроме этого MathCAD предоставляет возможность не задавать следующее значение, если шаг по величине совпадает со значением 1 или –1. В этом случае формат определения переменной можно представить в виде: Имя_переменной := начальное_значение .. конечное_значение Пример 3. Требуется определить переменную р, принимающую значения на интервале [0, 1] с шагом0,1. Решение. На рис. 5.8 представлены два фрагмента с решением поставленной задачи. На рис. 5.8, а представлено решение в соответствии с форматом, принятым для определения заданной переменной. А на рис. 5.8, b – такое же определение, но с введением вспомогательных переменных для обозначения и задания границ интервала, и величины шага, необходимых для определения переменной.
Рис. 5.8. Определение переменной, принимающей значения на интервале Пример 4. Требуется получить таблицу значений функции Решение. Решение задачи можно свести к выполнению следующих шагов:
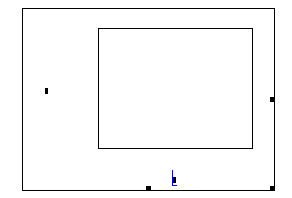
На рис. 5.9 представлен фрагмент документа с решением задачи 4.  Рис. 5.9. Получение таблицы значений функции на заданном интервале с постоянным шагом 5.11. Построение графиков в декартовой системе координатВсе основные типы графиков и инструменты работы с ними расположены на рабочей панели Graph_(График'>Graph (График) семейства Math (Математические). На этой панели вы можете найти ссылки на семь типов графиков. В данном разделе остановимся на декартовой системе координат. В MathCAD существует несколько способов построения графиков, однако, первый шаг для всех способов будет один и тот же. Этим первым шагом является введение специальной заготовки для будущего графика – так называемой графической области. Ввести графическую область, как для декартового, так и для любого другого графика можно либо с панели Graph (Графические), либо командой одноименного подменю меню Insert (Вставка). Графическая область представляет собой две вложенные рамки, как это показано на рис. 5.10, а. Во внутренней области отображаются непосредственно кривые зависимостей. Пространство между рамками служит для визуализации разного рода служебной информации. Графическую область можно увеличивать и уменьшать с помощью специальных маркеров, расположенных на ее внешней рамке. Перемещать по документу и удалять графические области можно точно так же, как простые формулы.
Рис. 5.10. Графическая область в декартовой системе координат После того как графическая область будет введена, в общем случае требуется задать два соразмерных вектора, определяющих значения координат точек. Сделать это можно различными способами. Наиболее простым и часто используемым методом задания координатной сетки является так называемый быстрый метод. При его применении пользователь задает только имя переменной и вид функции, а шкалы осей и величину шага между узловыми точками автоматически определяет система. Для построения графика функции по быстрому методу, необходимо выполнить следующую последовательность действий:
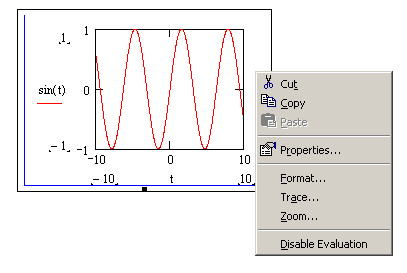
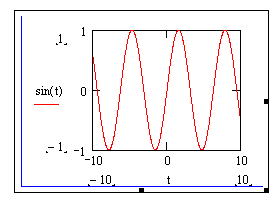
На рис. 5.10, b показан график функции y=sin(t), построенный по быстрому методу. К недостаткам рассматриваемого метода относится, прежде всего, то, что область изменения переменной для всех функций определяется одна и та же: от –10 до +10. В большинстве же случаев такие пределы будут неприемлемы по целому ряду причин. Например, если амплитуда экстремумов мала по сравнению с изменением величины функции на промежутке, что они становятся просто незаметными. Чтобы справиться с возникшими трудностями, нужно просто уменьшить интервал изменения либо переменной, либо функции. Для этого выделите графическую область щелчком левой кнопкой мыши. При этом визуализируются все элементы, которые до этого были скрыты (рис. 5.11, а).
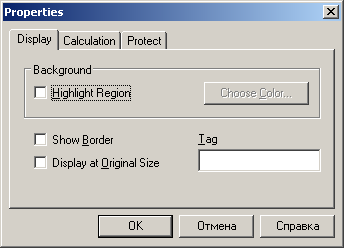
Рис. 5.11. Графическая область в декартовой системе координат Непосредственно под крайними значениями (для оси X) или слева от них (для оси Y) появятся цифры, отражающие максимальные и минимальные величины координат узловых точек графика. Чтобы изменить их значения, просто удалите (точно так же, как при редактировании формул) старые величины и введите новые. Изменения пределов по оси X вызывает автоматический пересчет крайних значений по Y. Однако если вы переопределите область по оси Y, то область изменения переменной останется старой. Графическую область можно отформатировать – изменить внешний вид и цветовую гамму. Для этого можно воспользоваться командой Свойства'>Properties (Свойства) из контекстного меню графика (вызывается щелчком правой кнопкой мыши на графической области), как это показано на рис. 5.11, b. В окне Properties(Свойства) для подавляющего большинства пользователей объективно могут быть полезны два параметра, расположенных на вкладке Display (см. рис. 5.11, b):
При исследовании функции большое применение находит команда Trace (След) из контекстного меню графика. Эта команда позволяет считать с графика текущее значение аргумента и соответствующего ему значение функции. В результате выполнения этой команды открывается окно «X-Y Trace», как это показано на рис. 5.12. Чтобы активизировать трассировку, нужно мышью щелкнуть по графику. В результате на графике появляются две линии – вертикальная и горизонтальная, которые легко с помощью мыши перемещаются по графической области, а координаты точки пересечения линий отражается в окне трассировки. 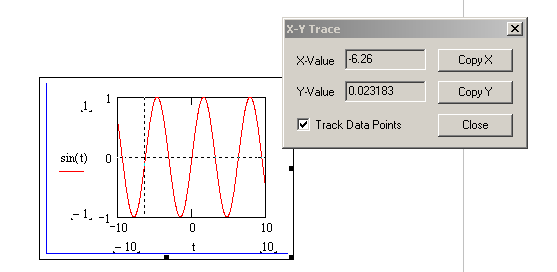 Рис. 5.12. Считывание координат точки на графике |