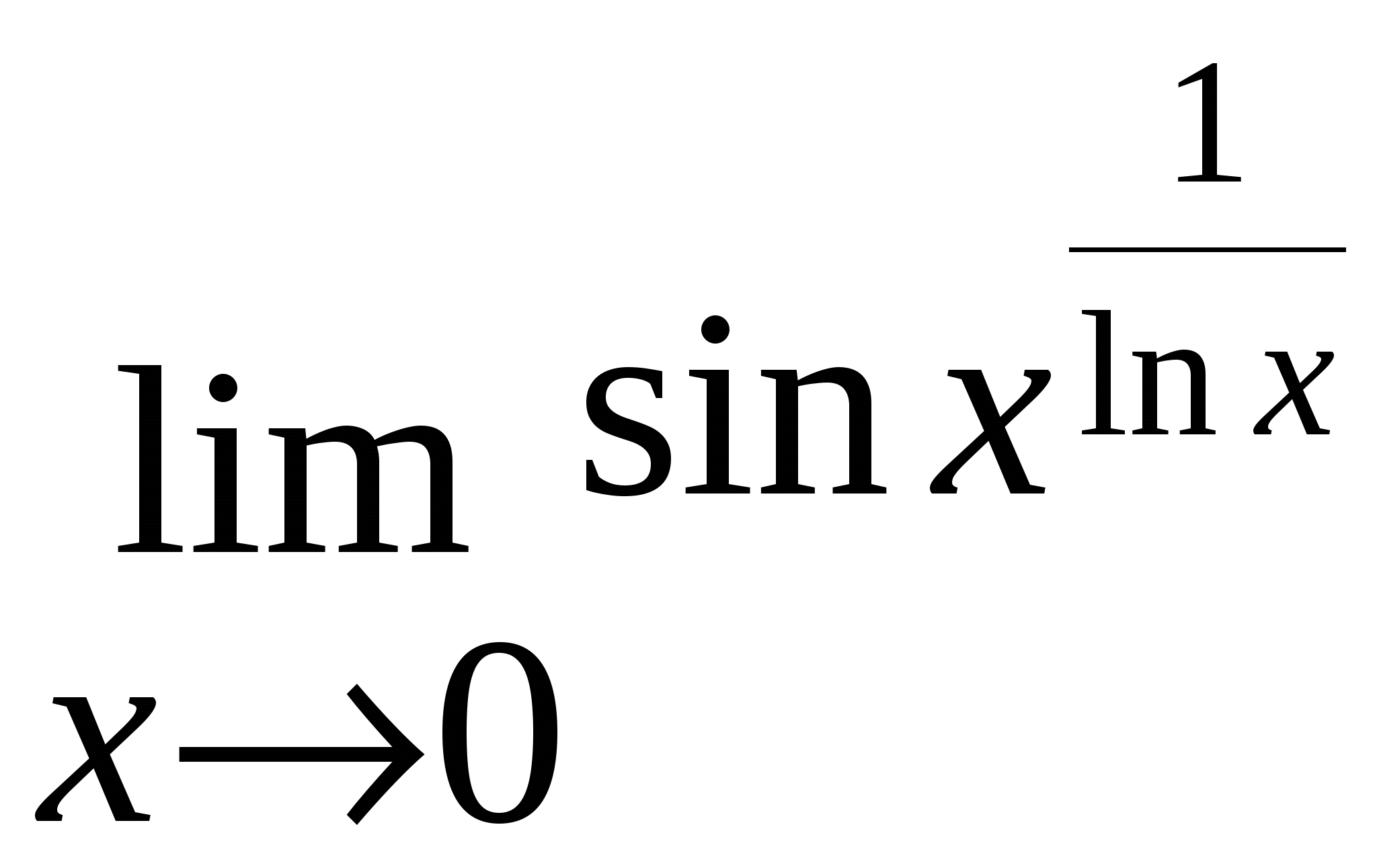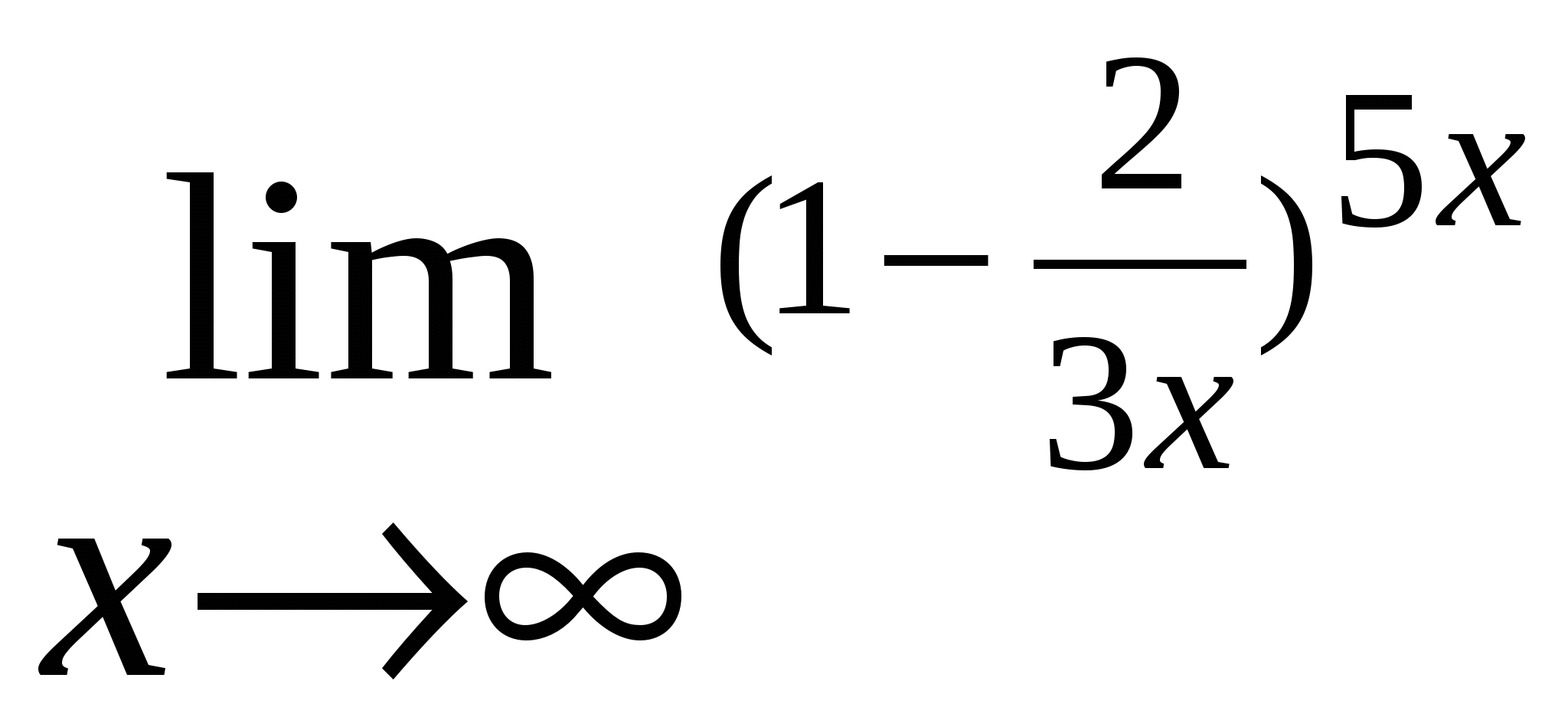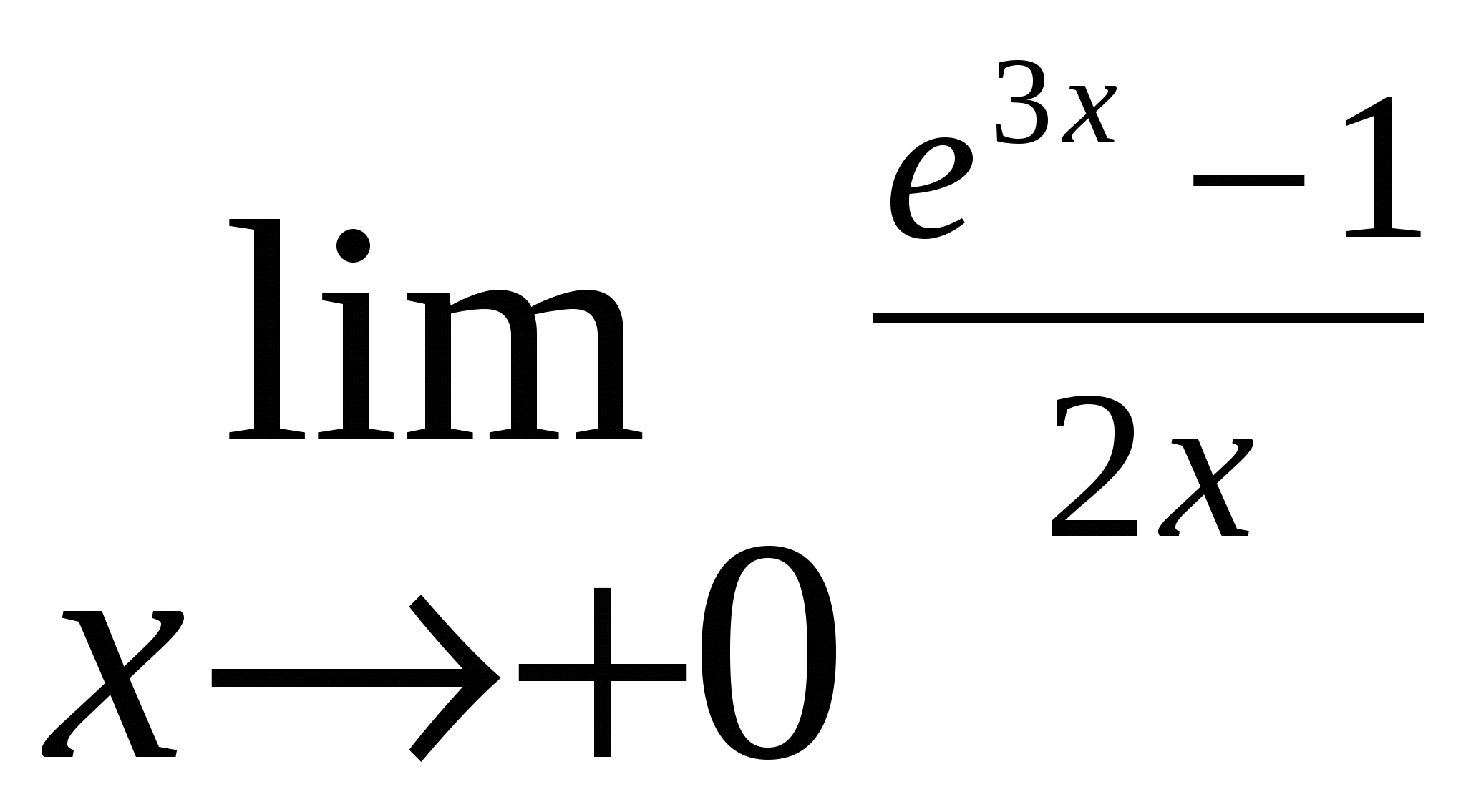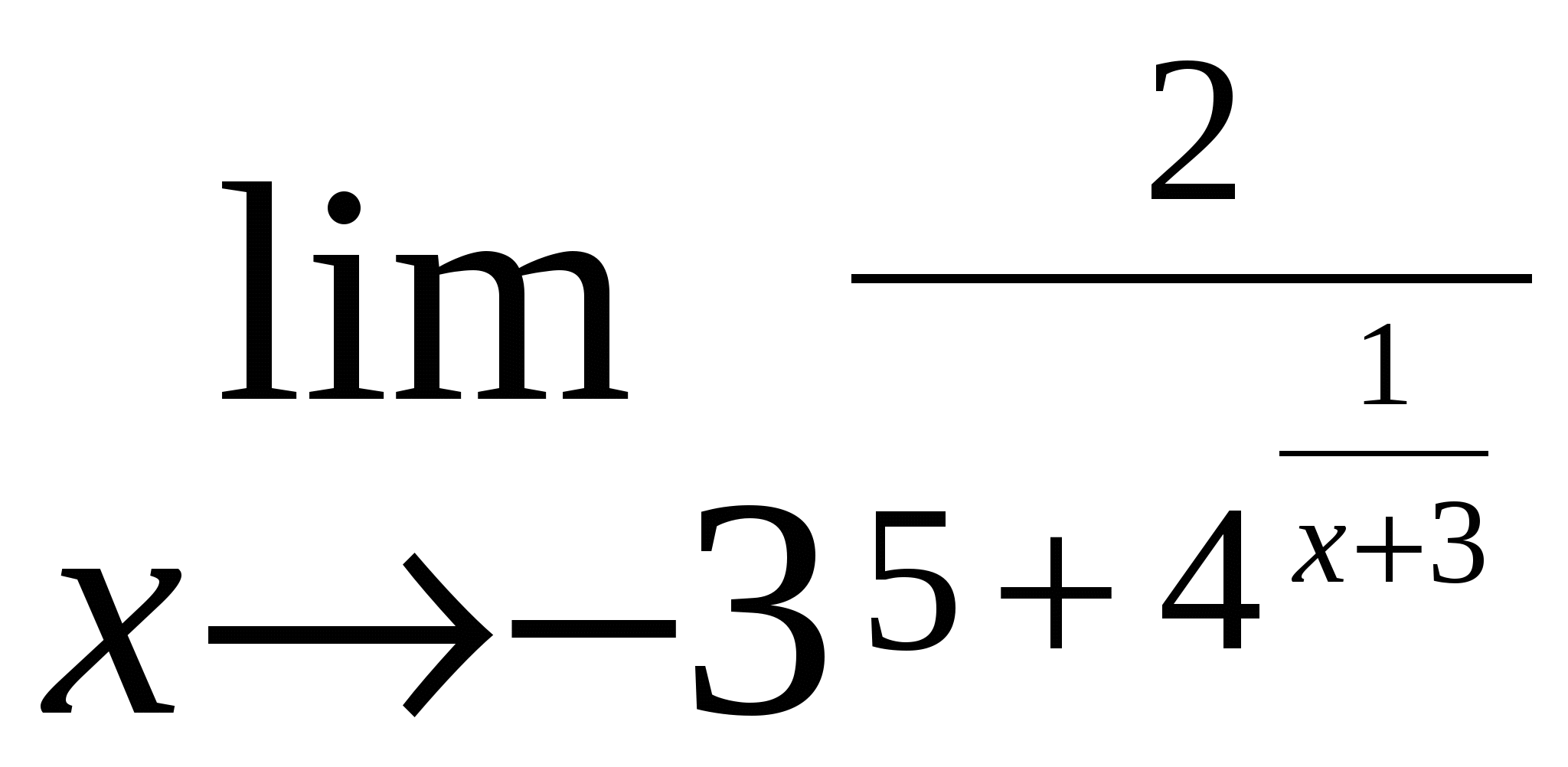ОСНОВЫ работы в MathCad. Основы работы в математическом пакете Mathcad

• Название: Основы работы в математическом пакете Mathcad
• Анкор: ОСНОВЫ работы в MathCad.doc
• Дата: 27.12.2017
• Размер: 8.94 Mb.
• Имя файла: ОСНОВЫ работы в MathCad.doc
• Тип: Документы; #13225
• страница: 7 из 12

6.3. Вычисление пределов и производных

Задача вычисления пределов может иметь самостоятельное значение. Ниже приведены примеры вычисления пределов от сложных функций.

Пример 12. Требуется вычислить следующие пределы [21]:


Решение. Для нахождения пределов достаточно обратиться к панели Calculus (Вычислить), на которых расположены кнопки с пределами, в том числе левосторонними и правосторонними. Выполненные команды предоставят шаблоны для заполнения, после чего следует выполнить команду Simplify (Упростить), предназначенную для символьных вычислений. Решение представлено на рис. 6.14.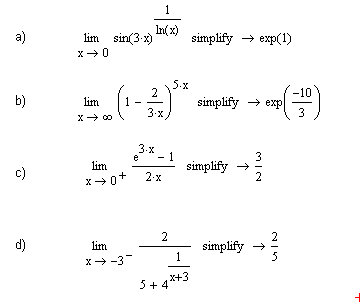


Рис. 6.14. Вычисление пределов
Пример 13. Требуется найти производные для заданных функций:

Решение. Для нахождения пределов достаточно обратиться к панели Calculus (Вычислить), на которых расположены команды для вычисления производных. Выполненные команды предоставят шаблоны для заполнения, после чего следует выполнить команду Simplify (Упростить), предназначенную для символьных вычислений. Для первой функции аналитическое выражение определено в виде функции, а во втором случае знак дифференцирования применен к аналитическому выражению. Решение представлено на рис. 6.15.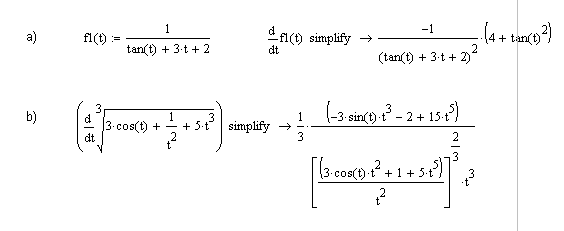



Рис. 6.15. Вычисление пределов

Пример 14. Требуется найти значение производной от функции в точке.

Решение. Для нахождения пределов достаточно обратиться к панели Calculus (Вычислить), на которых расположены команды для вычисления производных. Выполненные команды представлены на
рис. 6.16.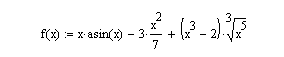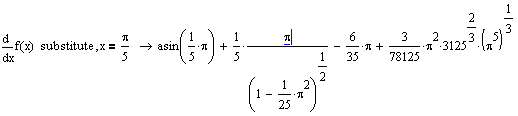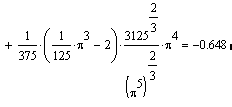






Рис. 6.16. Вычисление пределов

6.4. Решение систем трансцендентных уравнений

К настоящему времени разработано много методов решения систем уравнений. Для решения систем уравнений в системе MathCad предусмотрен, так называемый, блок решения. Он удобен тем, что при его использовании уравнения записываются в обычной форме, а также тем, что позволяет решать как системы линейных, так и системы нелинейных уравнений, причем, как в численном, так и символьном виде.

Последовательность действий при численном решении сводится к следующему:

1. 
   Задаются начальные значения для искомых переменных.
   
2. 
   Формируется блок решения, а именно: между ключевыми словами Given и find(список искомых переменных) записывается система уравнений. Напомним, что знак «=» при написании уравнений выделен цветом. Это – булевский знак! Его следует брать с панели Boolean.
   
3. 
   После конструкции find записывается знак «=».
   

При символьном решении задание начальных значений не требуется, а вместо знака «=» для решения следует использовать знак «».

Пример 15. Требуется найти точки экстремума функции .

Решение. Известно, что необходимым условием для существования экстремума – равенство нулю частных производных первого порядка. Поэтому на начальном этапе необходимо получить частные производные по переменной x и по переменной y и приравнять их нулю. Для вычисления производной можно воспользоваться соответствующей командой панели Calculus (Вычислить). После чего процесс решения задачи можно свести к процессу решения системы уравнений. На рис. 6.17 представлены фрагменты документа MathCAD, содержащие поиск экстремумов функции.

a)

b)

Рис. 6.17. Решение системы нелинейных уравнений в
задаче поиска экстремума
На рис. 6.17 представлены два варианта записи решения. На фрагменте, представленном на рис. 6.17, а, системы записаны в развернутом виде, а на рис. 6.17, b частные производные оформлены в виде функций и результаты решения заносятся в векторные значения.

Пример 16. Требуется найти точки пересечения параболы, заданной уравнением и прямой, заданной в виде: .

Решение. Предоставим два варианта решения задачи:

1. 
   решение с использованием блока решения;
   
2. 
   решение в графическом виде.
   

Вариант а

Поскольку точки пересечения линий являются общими для этих линий, то для определения точек пересечения следует решить систему из двух уравнений, описывающих эти линии. Если воспользоваться символьным блоком решения, то точки пересечения могут быть получены в виде, как это показано на рис. 6.18.

Рис. 6.18. Решение системы нелинейных уравнений в
задаче поиска экстремума
Поскольку используется символьный блок решения, для представления результатов в числовом виде используется команда float. Анализ полученных результатов показывает, что заданные линии пересекаются в двух точках с координатами (r, t) – (17.8, 3.49) и (10.0, –1.15).

Вариант b

Для получения графического решения представим уравнения линий в виде функций от одной из переменных. В качестве независимой переменной выберем переменную t, т.к. переменная r в данном случае входит в оба уравнения в первой степени. В результате придем сначала к двум уравнениям вида: и . А затем каждое из уравнений можно представить в виде функций, которые в дальнейшем будем использовать при построении графиков.

Изменение независимой переменной на начальном этапе будет взято «по умолчанию». Для уточнения координат точек пересечения выполняются следующие действия:

1. 
   переустанавливаются на графике диапазоны для изменения x и y;
   
2. 
   включается режим трассировки, путем щелчка правой кнопкой мыши на графике, выбор команды Trace… (Трассировка ...);
   
3. 
   активизирует окно с координатами трассировки – щелчок левой кнопкой мыши на графике;
   
4. 
   появившиеся координатные оси можно перемещать по графику от одной точки пересечения до другой.
   

На рис. 6.19 приведен фрагмент документа с графическим решением задачи – получение точек пересечения двух линий в декартовой системе координат.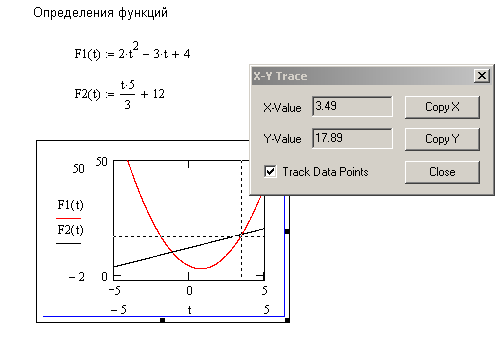

Рис. 6.19. Решение системы нелинейных уравнений в
задаче поиска экстремума
Анализ решений показывает, что результаты решений, произведенных разными способами, совпадают между собой.

При анализе систем нелинейных алгебраических уравнений важным обстоятельством явялется графическое построение систем функций.

Пример 17. Требуется построить график функции, заданной в параметрическом виде: .

Решение. Для построения графика функции, заданной в параметрическом виде, сначала нужно выбрать шаблон двумерного графика
X-Y Plot, в середине горизонтальных и вертикальных осей ввести функции Переменная может быть задана, как индексированная переменная. На рис. 6.20 представлены результаты построения требуемой функции.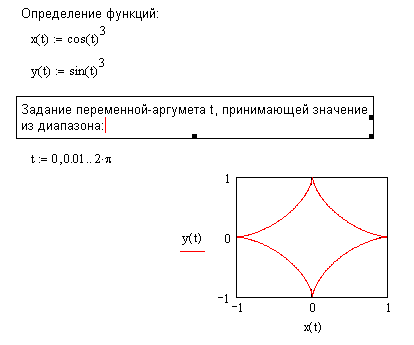



Рис. 6.20. График сложной функции, заданной парметрически