ОСНОВЫ работы в MathCad. Основы работы в математическом пакете Mathcad

• Название: Основы работы в математическом пакете Mathcad
• Анкор: ОСНОВЫ работы в MathCad.doc
• Дата: 27.12.2017
• Размер: 8.94 Mb.
• Имя файла: ОСНОВЫ работы в MathCad.doc
• Тип: Документы; #13225
• страница: 6 из 12

6.2. Решение неравенств

Для аналитического решения неравенств в MathCAD используется тот же самый оператор solve, расположенный на панели Symbolic (Символьные), что и для решения уравнений.

Пример 5. Требуется решить неравенство вида: в символьном виде.

Решение. Процесс решения задачи можно свести к выполнению следующих шагов:

1. 
   Выполнить команду solve, расположенную на панели Symbolics (Символьные).
   
2. 
   Заполнить предоставленный шаблон.
   
3. 
   Проанализировать результат.
   
4. 
   Решение неравенства из примера 5 предоставлено системой в виде, как это показано на рис. 6.10.
   

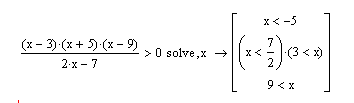Рис. 6.10. Решение неравенства
Полученное решение соответствует следующей записи в стандартной форме: .
Как вы уже, наверное, заметили, MathCAD выдает ответы в несколько отличном, от принятом в нашей математике, виде. Поэтому зачастую самой трудной частью работы при символьном решении неравенств является интерпретация результата. Тут нужно запомнить несколько правил:

1. 
   Ответ оператор solve возвращает в виде вектора, содержащего элементарные неравенства. Каждое такое неравенство описывает область, в которой решаемое неравенство справедливо.
   
2. 
   Если область открытая (то есть одной из ее границ является бесконечность), то задающее ее элементарное неравенство будет иметь вид х>а или х<а. В стандартном виде такие области запишутся как или .
   
3. 
   Если область замкнута и ее границам соответствуют значения аргумента а и b, то она будет описана элементарным неравенством вида . В стандартном виде эта запись будет выглядеть как .
   
4. 
   Области в векторе ответа будут расположены строго в направлении числовой оси. Поэтому преобразовывать в стандартную форму его можно чисто механически, сохраняя исходный порядок областей. Для объединения обозначений областей в одно выражение используется символ «».
   

Пример 6. Требуется найти область определения функции .

Решение. Как известно, под областью определения функции понимают совокупность значений аргумента, при которых выражение, определяющее функцию, имеет смысл. Область определения заданной функции определяется из следующих условий:

• 
  аргумент логарифма может принимать только положительные значения;
  
• 
  знаменатель у дроби, стоящей под знаком логарифма не должен обращаться в нуль (х2);
  
• 
  числитель не должен обращаться в нуль (х1).
  

На начальном этапе можно решить неравенство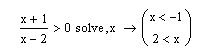. А затем из полученной области исключить точки –1 и 2. Решение неравенства:

Что соответствует области: . В исключении точек
–1 и 2 нет необходимости, так как они не входят в означенную область.

Пример 7. Требуется найти область определения функции. Если имеются точки разрыва, то установить тип разрыва.

Решение. Поскольку аналитическое выражение функции представлено в виде дроби, а знаменатель дроби не может быть равен 0, из области определения функции следует исключить точку 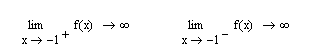, т.е. . Т.е. точка является точкой разрыва. Чтобы найти тип разрыва следует найти односторонние пределы (команды следует взять с панели Calculus (Вычислить)):



Вывод. Так как односторонние пределы равны , то имеет место неустранимый разрыв 2-го рода, а точка является точкой бесконечного скачка функции.

Пример 8. Требуется найти все асимптоты графиков функции. Найти подтверждение правильности решения на графике функции.

Решение. Известно, если точка 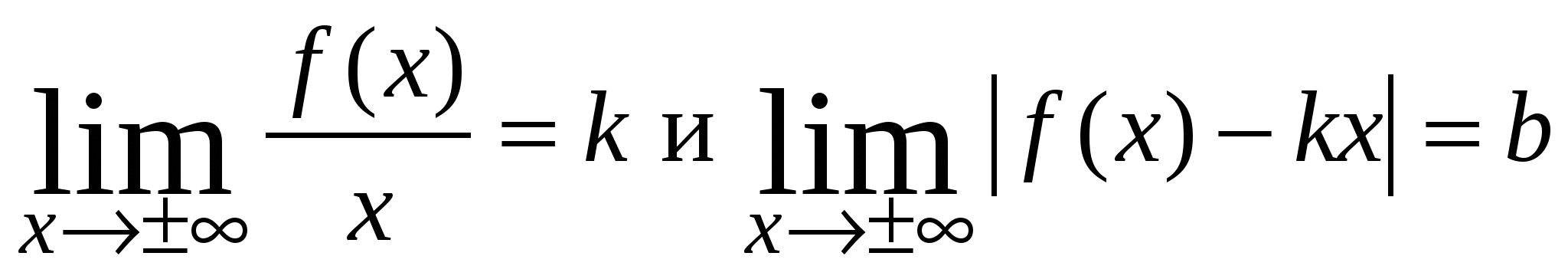является точкой бесконечного разрыва функции, то прямая есть вертикальная асимптота графика функции. В предыдущем примере было установлено, что точка является такой точкой бесконечного разрыва. Следовательно, прямая является вертикальной асимптотой графика заданной функции. Для получения наклонных асимптот нужно вычислить пределы: . Если эти пределы существуют, то прямая есть наклонная асимптота графика функции. Вычисление пределов и уравнение наклонной асимптоты представлены на
рис. 6.11.




Рис. 6.11. Вычисление параметров наклонной асимптоты

Таким образом, уравнение наклонной асимптоты имеет вид: . Анализ построенного графика функции и ее асимптот, представленного на рис. 6.12, показывает, что расстояния текущей точки кривой до каждой из асимптот стремится к нулю по мере удалении этой точки по кривой в бесконечность, что соответствует определению асимптоты.

Следует обратить внимание на формулу в определении вертикальной асимптоты, представленной на рис. 6.12. Здесь значение функции равно х, а область аргумента соответствует постоянному значению –1.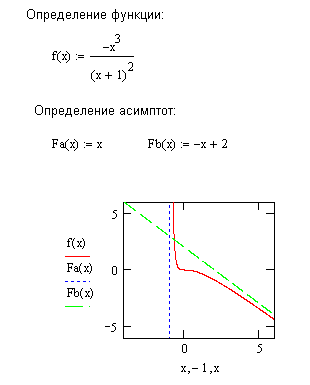



Рис. 6.12. Графическая интерпретация связи графика с асимптотами

Пример 9. Требуется на графике функциинайти точки, подозрительные на экстремум (критические точки).

Решение. Воспользуемся необходимым условием существования экстремума: если функция непрерывна в точке х₀ и ее окрестности и принимает в этой точке экстремальное значение, то первая производная f’(х₀) либо равна нулю или бесконечности, либо не существует. Следовательно, для того, чтобы найти точки, подозрительные на экстремум, следует найти решение уравнений: 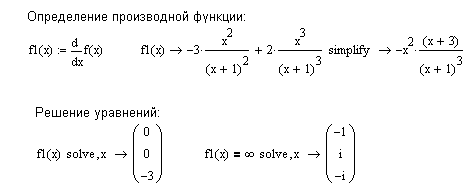и . Решение представлено на рис. 6.13.


Рис. 6.13. Определение критических точек графика функции

Из предоставленных решений берем только действительные корни:

.

Пример 10. Требуется на графике функциинайти точки, подозрительные на точки перегиба. Найти подтверждение правильности решения на графике функции.

Решение. Необходимое условие точки перегиба: если х₀ – точка перегиба кривой y=f(х), то вторая производная f’’(х₀) либо равна нулю или бесконечности, либо не существует. Решение представлено на
рис. 6.14. На рис. 6.15 изображены функция и ее вторая производная.



Рис. 6.14. Определение точек перегиба графика функции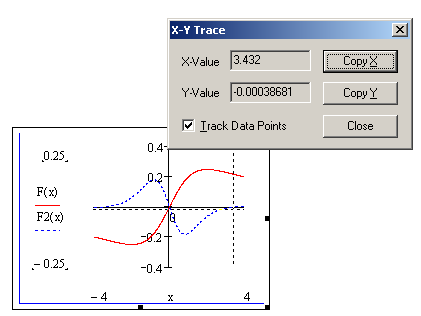



Рис. 6.15. Графика функции F(x) и ее второй производной F2(x)
Пример 11. Требуется найти максимум функции при ограничениях, заданных неравенствами вида: .

Решение. Для решения поставленной задачи можно воспользоваться следующей схемой [20]:

1. 
   Определить функцию.
   
2. 
   Задать начальные условия.
   
3. 
   Инициировать блок решения, в котором:
   

1. 
   Задать ограничения.
   
2. 
   Вычислить максимальное значение функции с помощью стандартной функции maximize, описанной в примере 2 главы 5.
   

4. 
   Отобразить результат вычислений.
   

Решение представлено на рис. 6.16.

Рис. 6.16. Решение неравенства