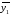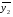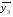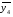Основы теории надёжности
 Скачать 0.92 Mb. Скачать 0.92 Mb.
|
|
ГЛАВА 7. Надёжность элементов механизма. §1. Надёжность подшипников качения. Вероятность безотказной работы отождествляется с вероятностью выполнения известного условия 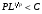 где P – приведенная нагрузка на подшипник: 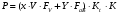 L – заданный ресурс: 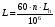 (млн. об.) (млн. об.)Р – показатель степени: Р = 3 для шарикоподшипников Р=10/3 для роликоподшипников В отличие от обычных расчётов, Р рассматривают как случайную величину, 90% динамического и грузоподъемного значения которой приводятся в каталогах и обозначается как С90 Среднее значение динамической грузоподъемности: 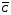 = 1,46 = 1,46 С90 – для роликоподшипников С90 – для роликоподшипников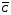 =1,52 =1,52 С90 – для шарикоподшипников С90 – для шарикоподшипниковПолагаем, что приведенная нагрузка Р и динамическая грузоподъемность С распределены по нормальному закону. Тогда вероятность безотказной работы определяем по квантили нормированного нормального распределения. 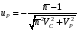 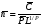 , т.е. , т.е. 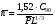 и и 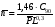 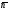 – коэффициент запаса по средним нагрузкам; – коэффициент запаса по средним нагрузкам;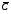 – среднее значение динамической грузоподъемности; – среднее значение динамической грузоподъемности;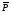 -среднее значение приведенной нагрузки; -среднее значение приведенной нагрузки;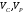 – коэффициенты вариации динамической грузоподъемности и приведенной нагрузки. – коэффициенты вариации динамической грузоподъемности и приведенной нагрузки.Среднее значение приведенной нагрузки 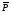 вычисляют по обычным зависимостям, в которые представляют средние значения радиальной и осевой нагрузок, действующих на подшипник. вычисляют по обычным зависимостям, в которые представляют средние значения радиальной и осевой нагрузок, действующих на подшипник.Коэффициент вариации приведенной нагрузки 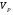 принимают равным коэффициенту вариации внешней нагрузки, действующей на подшипник, ввиду их линейной зависимости. принимают равным коэффициенту вариации внешней нагрузки, действующей на подшипник, ввиду их линейной зависимости.Коэффициент вариации динамической грузоподъемности VС принимают равным VС = 0,25 - для роликоподшипников VС = 0,27 - для шарикоподшипников Распределение ресурса подшипников подчиняется закону Вейбулла. В соответствии с этим законом связь между вероятностью безотказной работы 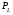 и ресурсом L выражается зависимостью и ресурсом L выражается зависимостью 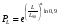 где L90 — 90% ресурс = 1,5 — параметр формы кривой распределения Вейбулла, связанный с распределением ресурса. В расчётах подшипников качения отношение 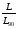 называют коэффициентом надёжности называют коэффициентом надёжности 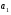 , который определяется по формуле, вытекающей из предыдущего выражения: , который определяется по формуле, вытекающей из предыдущего выражения: 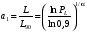 Учитывая, что между ресурсом L и динамической грузоподъёмностью C существует соотношение 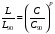 получаем получаем 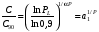 P = 3 – шарикоподшипниковый P = 10/3 – роликоподшипниковый Среднее значение грузоподъёмности 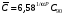 Среднеквадратическое отклонение динамической грузоподъёмности: 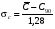 Коэффициент вариации динамической грузоподъёмности 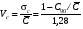 Средний ресурс: 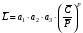 a1 – коэффициент надёжности; a2 – коэффициент материала; a3 – коэффициент смазки; Р = 3 – шарикоподшипниковый; Р = 10/3 – роликоподшипниковый; Пример расчёта: определить вероятность безотказной работы роликоподшипника № 2207, нагруженного случайной радиальной силой, коэффициент вариации которой 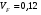 , частота вращения внутреннего кольца подшипника n = 300мин-1, требуемый ресурс , частота вращения внутреннего кольца подшипника n = 300мин-1, требуемый ресурс 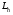 = 3500 час. Среднее значение приведённой нагрузки = 3500 час. Среднее значение приведённой нагрузки 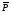 = 4500 Н = 4500 НРешение: 1. По каталогу-справочнику определяем 90% динамической грузоподъёмности: С90 = 25600Н 2. Вычисляем заданный ресурс: 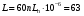 3. Находим среднее значение динамической грузоподъёмности: 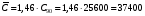 Н Н4. Определим коэффициент запаса по средним значениям: 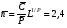 5. Коэффициент вариации эквивалентной динамической нагрузки принимаем равным коэффициенту вариации внешней нагрузки: Vp= VF= 0,12 6. Квантиль нормированного нормального распределения определяется по формуле: 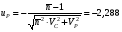 7. По таблицам нормального распределения в зависимости от полученной 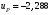 находим, что вероятность безотказной работы рассчитываемого подшипника находим, что вероятность безотказной работы рассчитываемого подшипника 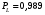 §2. Надёжность зубчатых передач. Вероятность безотказной работы 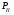 по критерию сопротивления контактной усталости определяем как вероятность того, что контактное напряжение H не превышает предела контактной выносливости (предельного значения расчетного параметра) по критерию сопротивления контактной усталости определяем как вероятность того, что контактное напряжение H не превышает предела контактной выносливости (предельного значения расчетного параметра) 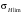 : :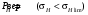 Контактное напряжение 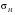 , действующее в полюсе зацепления: , действующее в полюсе зацепления: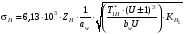 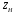 — коэффициент, учитывающий форму сопряженных поверхностей; — коэффициент, учитывающий форму сопряженных поверхностей;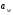 — межосевое расстояние, мм; — межосевое расстояние, мм;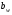 — рабочая ширина венца, мм; — рабочая ширина венца, мм;U — передаточное число; 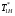 — крутящий момент на шестерне при работе в номинальном режиме (номинальный момент), — крутящий момент на шестерне при работе в номинальном режиме (номинальный момент), 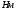 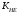 – коэффициент нагрузки – коэффициент нагрузки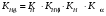 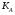 — коэффициент внешней нагрузки; — коэффициент внешней нагрузки;KH — коэффициент, учитывающий распределение нагрузки по ширине венца; KHV — коэффициент, учитывающий динамическую нагрузку, возникающую в зацеплении; KH — коэффициент, учитывающий распределение нагрузки между зубьями; Номинальный момент 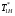 и другие параметры в формуле для H считаем детерминированными величинами. и другие параметры в формуле для H считаем детерминированными величинами.Полагаем, что KА, KH, KH, KH не коррелированны (не взаимосвязаны), тогда коэффициент вариации равен 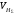 равен: равен: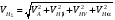 VА, VH, VHV, VH - коэффициенты вариации соответствующих величин KА, KH, KHV, KH . VА выбирается по таблице 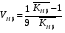 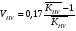 при H > HB350 при H > HB350 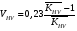 при H при H 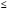 HB350 HB350 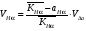 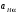 — предельная величина, зависящая от коэффициента перекрытия; — предельная величина, зависящая от коэффициента перекрытия;a — разность шагов зацепления; 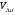 – коэффициент вариации разности шагов зацепления: – коэффициент вариации разности шагов зацепления:Обычно принимают 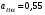 ; ; 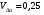 ; ; 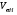 — коэффициент вариации контактного напряжения — коэффициент вариации контактного напряжения 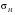 : :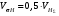 Коэффициент вариации предела контактной выносливости принимается несколько больше, чем для базового образца: 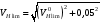 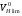 – коэффициент вариации для базового образца – коэффициент вариации для базового образцаВероятность безотказной работы по критерию сопротивления контактной усталости 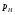 определяется по таблице в зависимости от величины квантили определяется по таблице в зависимости от величины квантили 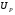 : :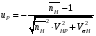 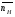 – коэффициент запаса прочности по средним напряжениям, равный: – коэффициент запаса прочности по средним напряжениям, равный: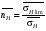 Пример расчёта: для цилиндрической прямозубой передачи рассчитать вероятность безотказной работы по критерию сопротивления контактной усталости. Среднее значение контактного напряжения 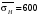 МПа. МПа.Средние значения частных коэффициентов  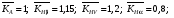 Коэффициент вариации VА = 0,1 Среднее значение предела выносливости 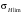 = 780 МПа = 780 МПаРешение: 1. Oпределяем коэффициент вариации частных коэффициентов напряжения 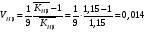 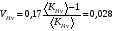 VH = 0,05 2. Определить коэффициент вариации нагрузки 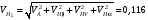 3. Находим коэффициент вариации контактного напряжения 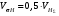 = 0,5 = 0,5 0,116 = 0,058 0,116 = 0,0584. Принимаем коэффициент вариации базового образца 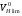 = 0,09 и определяем коэффициент вариации зубчатого колеса = 0,09 и определяем коэффициент вариации зубчатого колеса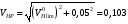 5. Коэффициент запаса прочности по средним напряжениям равен: 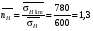 6. Квантиль нормального распределения равен 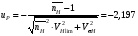 7. По таблицам зависимости от 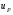 определим вероятность безотказной работы по критерию сопротивления контактной усталости определим вероятность безотказной работы по критерию сопротивления контактной усталости 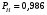 . .ГЛАВА 8. Научное планирование эксперимента. §1. Общие положения. Под научным планированием экспериментов понимают математическое установление оптимального плана их проведения. Основным требованием при организации любого эксперимента является минимизация времени и числа испытаний при сохранении требуемой достоверности результатов. Объект исследования X1 X2 факторы отклик Используя кибернетический подход, объект исследований рассматривают как «чёрный ящик», у которого известны входные и выходной параметры, но не известно внутреннее устройство. Входные параметры называют факторами, выходной параметр – откликом. Факторы рассматривают как детерминированные величины 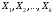 , отклик – как случайную величину Y. , отклик – как случайную величину Y.Обычно полагают, что закон распределения Y известен из теоретических соображений или экспериментальных исследований. Уравнение, связывающее отклик с факторами Y= (X1,X2) называют функцией отклика. Цель эксперимента — оценка наиболее простым способом функции отклика. В такой постановке эксперимент называют интерполяционным, основанным на интерполяции — нахождении функции по некоторым её значениям. Более сложным является экстремальный эксперимент, предназначенный для определения оптимума. Критерий оптимальности формируется исследователем. Примером экстремальных экспериментов в области деталей ТО могут служить: оптимизация состава антифрикционных сплавов и покрытий, металлокерамических материалов, пластмасс для отдельных групп элементов технологического оборудования. §2. Функция отклика. Вид функции отклика (линейная, степенная, логарифмическая и т.д.) или математическую модель объекта исследования устанавливают, исходя из физических представлений о самом объекте или на основе опыта предыдущих исследований. При отсутствии таких сведений функцию отклика представляют результатом её разложения в ряд Тейлора, т.е. использую модель в виде полинома. В простейшем случае выбирают полином первого порядка, линейный по всем переменным 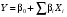 , где 0 и i — коэффициенты функции. , где 0 и i — коэффициенты функции.Функция отклика несколько усложняется, если необходимо учитывать взаимодействие факторов: 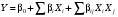 Для описания области, близкой к оптимуму, выбирают полином второго порядка 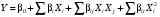 ; ;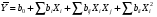 Значения факторов удобно задавать в относительных величинах: (1) — max, min; 0 — средний. В общем случае значение факторов равно: 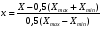 , ,где Xmax, Xmin — максимальное и минимальное абсолютные значения фактора, т.е. пределы варьирования фактора в эксперименте; X — абсолютное значение фактора. К исследуемым факторам предъявляют следующие требования: Управляемость — возможность установления и поддержания фактора на выбранном уровне; Независимость — возможность устанавливать фактор на выбранном уровне вне зависимости от уровней других факторов; Совместимость — все комбинации факторов осуществимы и безопасны. §3. Выбор числа уровней факторов. Планирование эксперимента в основном сводится к выбору числа уровней факторов и определённого значения каждого фактора в опыте. Выбранное число уровней p в сочетании с числом факторов k определяют число возможных опытов N, которое равно: 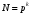 . .Если каждый опыт повторяют m раз, то число образцов соответственно равно 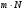 . .Число повторений m может быть выбрано по таблицам на основе задания допустимой ошибки и доверительной вероятности. Эксперимент, в котором реализуются все возможные сочетания значений факторов, называют полным факторным экспериментом (ПФЭ). §4. Двухфакторный эксперимент. Для линейной модели достаточно варьирование факторов на двух уровнях. В этом случае имеем ПФЭ типа 2k. Графический план такого эксперимента для двух факторов можно представить в координатах кодированных значений факторов X1 и X2. X1 X2 1 2 3 4 Условия проведения опытов соответствуют вершинам квадрата. Для первого опыта X1 = +1; X2 = –1; второго – X1 = +1; X2 = +1; третьего – X1 = –1; X2 = +1; четвёртого – X1 = – 1, X2= – 1.
План эксперимента можно задавать таблицей, называемой матрицей плана. Более исчерпывающая информация об эксперименте представляется матрицей для планирования эксперимента. Для ПФЭ типа 22 матрица планирования включает матрицу плана эксперимента, значения фиктивного фактора X0, эффект взаимодействия факторов X1 и X2 и значения отклика.
Формулы для определения оценок b0, bi, bij неизвестных коэффициентов 0, i, ij функции отклика имеют вид: 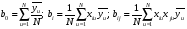 где 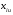 , ,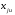 – величины i-го и j-го факторов (i j; i,j= 1,2,…,k) в u-м опыте. – величины i-го и j-го факторов (i j; i,j= 1,2,…,k) в u-м опыте.Среднее значение отклика 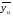 в u-м опыте определяется по формуле в u-м опыте определяется по формуле 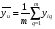 где m – число повторов опытов; yuq – текущее значение отклика в u-м опыте при q-м повторе. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||