Основы теории надёжности
 Скачать 0.92 Mb. Скачать 0.92 Mb.
|
|
ГЛАВА 5. Резервирование как метод повышения надёжности §1. Надёжность сложных систем. Под элементом будем понимать составную часть сложной системы, которая может характеризоваться самостоятельными входными и выходными параметрами. Двухступенчатый зубчатый редуктор. 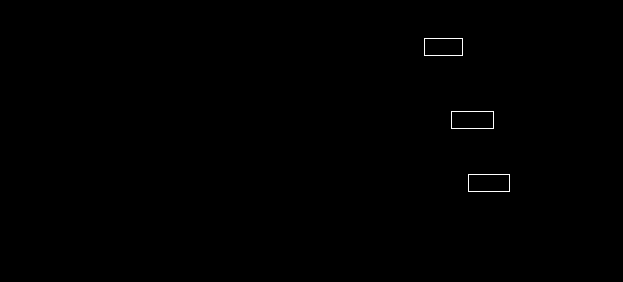  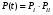 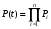 Если причина выхода из строя элемента т.о. связана только с внезапными отказами, которые подчинены экспоненциальному закону, то: 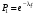 ; ; 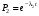 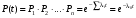 , ,где 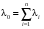 . .§2. Резервирование ненадёжных элементов. Для повышения надёжности сложных систем можно применять резервирование, т.е. создавать дублирующие элементы. При выходе из строя одного из элементов, дублёр выполняет его функции , элемент, таким образом не прекращает работу.  При постоянно нагруженном резерве резервные элементы находятся в одинаковом режиме работы с основным элементом. Схема расчета вероятности безотказной работы Пусть 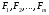 – вероятность появления отказа каждого из элементов за время T. – вероятность появления отказа каждого из элементов за время T. Отказ всей системы – сложное событие, которое будет иметь место при условии отказа всех элементов системы. Вероятность совместного появления всех отказов F(t) по теореме умножения вероятностей будет: 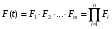 Тогда вероятность безотказной работы всей системы с параллельно резервированными элементами будет равна: 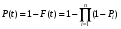  P(t)=1-(1-0,9)2=1-0,01=0,99 При m=2 P(t)=0,99 m=3 P(t)=0,999 m=4 P(t)=0,9999 Возможно создание ненагруженного резервирования (резервирования замещением), когда резервные цепи находятся в отключенном состоянии и включаются лишь в том случае, если основной элемент отказывает. Для нагруженного резерва надёжность резервных элементов не зависит от того, в какой момент времени они включились на место основного. Ненагруженные резервные элементы не работают до момента их включения вместо основного элемента. В этот период их отказ невозможен. §3. Задача о расчёте надёжности элемента с восстановлением (задача Гнеденко Б.В.). При отказе основного элемента его замещает резервный, а основной элемент начинает восстанавливаться (ремонтируется или заменяется), после чего становится в резерв. Отказ пары (элемента и дублёра) наступит тогда, когда на каком-либо цикле, во время восстановления одного элемента, отказывает другой. Пусть - интенсивность отказа основного элемента, а p – интенсивность отказа резервного элемента и G(t) – закон распределения времени ремонта. При малой вероятности 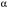 отказа пары на одном цикле, вероятность безотказной работы всей системы может быть выражена приближенной формулой: отказа пары на одном цикле, вероятность безотказной работы всей системы может быть выражена приближенной формулой: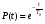 , , 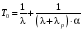 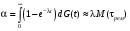 где 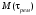 – математическое ожидание времени ремонта. – математическое ожидание времени ремонта.§4. Резервирование систем. Резервирование бывает общим или раздельным. Общее резервирование означает, что при выходе из строя любого элемента, включается резервная цепь, которая полностью заменяет данную. Раздельное резервирование обеспечивает возможность включения резервного элемента при выходе из строя любого элемента системы. Рассмотрим более подробно две эти схемы. Общее резервирование.  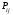 – вероятность безотказной работы одного элемента – вероятность безотказной работы одного элементаПервая цепь 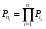 ; вторая цепь ; вторая цепь 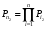 Вероятность безотказной работы всей системы: 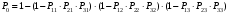 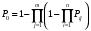 Раздельное резервирование. Та же цепь, но каждый элемент имеет свой резерв.  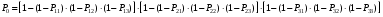 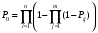 Это резервирование является наиболее эффективным. В соответствии с государственными стандартами показатели системы нормируются.
§5. Примеры расчёта надёжности с резервированием и без. Пример1. Определение вероятности безотказной работы привода, состоящего из электродвигателя, упругой муфты и двухступенчатого зубчатого редуктора.  Дано: P1 = 0,99 – вероятность безотказной работы ЭД P2=0,9973 – вероятность безотказной работы муфты P3,6,9 = 0,999 - вероятность безотказной работы валов Р4,7,10 = 0,99 - вероятность безотказной работы подшипников Р5,8 = 0,9973 - вероятность безотказной работы зубчатых передач РМ = 0,9999 - вероятность безотказной работы масла Расчёт: составляем структурную схему вероятностного расчёта 1 2 3 4 5 6 7 8 9 11 10 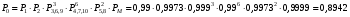 Пример 2. Определение вероятности безотказной работы привода, состоящего из электродвигателя, упругой муфты, двухступенчатого зубчатого редуктора, выполненного по соосной схеме с резервированием на полную мощность. Исходные данные применяются как в примере 1.  Расчёт: составляем структурную схему вероятностного расчёта. 2 3 4 1 6 8 10 12 5 7 9 11 13 14 15 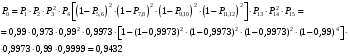 Примечание: Несмотря на то, что надёжность привода с резервированием выше на 5,5%, чем без резервирования, она так же невелика, что является следствием увеличения числа подшипников, вероятность безотказной работы которых принята весьма низкой из-за отсутствия методов расчёта на вероятность, большую чем 0,99. ГЛАВА 6. Диагностика технических объектов. §1. Задачи технической диагностики. Весьма важно иметь методы и средства для оценки технического состояния объекта, т.е. определения степени удалённости оценки от предельного состояния, выявления причин нарушения работоспособности, установления вида и места возникновения повреждения и т.п. Все эти задачи решаются методами диагностирования, применение которых позволяет получить большой экономический эффект за счёт более полного использования потенциальных возможностей т.о. Результаты диагностирования могут быть использованы для прогнозирования надёжности объекта и для принятия решения о проведении ремонта. Диагностические признаки:
Величины износа, деформации, вакуум являются теми диагностическими признаками, по которым можно сделать вывод о техническом состоянии объекта. В общем случае должен быть осуществлён поиск неисправностей, например методом последовательных разбиений всего множества элементов на две части. 1 1/2 1/2 1/4 1/4 испр. неиспр. испр. неиспр. Неисправную часть снова разбивают на две и продолжают анализ до тех пор, пока не будет обнаружено место повреждения. 3. Контроль работоспособности изделия по косвенным признакам производится в том случае, когда непосредственно измерение выходных параметров затруднено. Косвенными диагностическими признаками могут служить: изменения температуры, наличие в смазке продуктов износа. §2.Диагностирование сложных систем. Для диагностической модели входным параметром X будет значение показателя качества изделия, а входным параметром некоторый диагностический параметр – диагностический сигнал 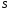 . .В общем случае в векторной форме можно записать 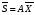 , ,где A-оператор, характеризующий те преобразования, которые необходимо осуществить с величиной Х, чтобы получить S. По совокупности значений множества параметров судят о принадлежности объекта к тому или иному классу: 1 класс: объект работоспособен 2 класс: объект работоспособен, но требует подналадки. 3 класс: объект неработоспособен и требует ремонта. §3. Структура системы диагностирования. В общем виде можно представить следующую структурную схему диагностики технических элементов: формирование эталонных значений самоконтроль тестовые воздействия оценка состояния принятие решения обработка информации первичные преобразования объект диагностики Датчики (преобразователи), установленные на объекте диагностирования, передают разнообразные сигналы, которые преобразуются в электрические величины и поступают в блок обработки информации и оценки состояния изделия или характера изменения его параметров. Для всех сигналов, с которыми необходимо сравнивать поступающие диагностические сигналы, предусматривается массив допустимых эталонных значений. В некоторых случаях, чтобы оценить техническое состояние объекта, на него подаются специальные тестовые воздействия для оценки реакции объекта диагностики. Для повышения достоверности получаемых данных осуществляется самоконтроль путем повторного выполнения отдельных операций (повторная диагностика) и сравнение полученных данных. §4. Диагностика технологических устройств на основе применения формулы Байеса. Задача ставится следующим образом: известны состояния системы, включающие нормальные и типовые состояния неисправностей и их вероятностей. Произведены наблюдения в эксплуатации или испытания, в результате чего зафиксированы некоторые признаки. Спрашивается, как в связи с этим изменятся (уточняться) вероятности состояния системы? Признаки: — нагрев — увеличение времени разгона — увеличение погрешности изделий (позиционирования). Для анализа необходимы статистические сведения о частости наблюдения отдельных признаков при каждом типовом состоянии системы. Эти частости в дальнейшем рассматриваются как вероятности. Вероятность сложного события возникновения состояния и проявления комплекса 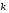 признаков признаков 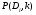 , согласно теореме умножения вероятностей: , согласно теореме умножения вероятностей: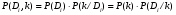 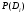 – априорная (известная) вероятность состояния Di; – априорная (известная) вероятность состояния Di;P(k/Di) – условная вероятность возникновения комплекса признаков k; P(k) – полная вероятность возникновения комплекса признаков в системе; P(Di/k) – условная вероятность состояния Di при комплексе признаков k; Отсюда, отбрасывая левую часть, получаем: 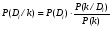 Состояние 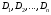 образуют полную группу несовместных событий, т.е. событий, из которых реализуется только одно. образуют полную группу несовместных событий, т.е. событий, из которых реализуется только одно. Полная вероятность появления комплекса признаков k в системе равна сумме вероятностей появления этого комплекса признаков при отдельных состояниях. 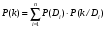 Подставляя 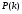 , получим формулу Байеса для вероятности некоторого состояния Di при комплексе признаков , получим формулу Байеса для вероятности некоторого состояния Di при комплексе признаков 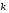 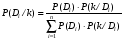 Комплекс признаков 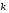 рассматривается состоящим из признаков рассматривается состоящим из признаков 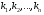 , которые полагаются независимыми. , которые полагаются независимыми. Тогда вероятность 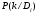 рассматривается как вероятность сложного события, равная произведению вероятностей простых событий: рассматривается как вероятность сложного события, равная произведению вероятностей простых событий: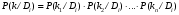 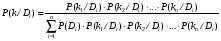 Если некоторые признаки являются зависимыми, то формула трансформируется. Например, если для состояния 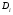 зависимыми являются признаки зависимыми являются признаки 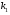 и и 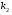 , то в формулу вместо произведения , то в формулу вместо произведения 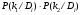 подставляют подставляют 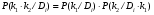 . .При использовании формулы, отсутствие какого-либо признака, например, 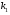 , рассматривается как противоположное событие с вероятностью , рассматривается как противоположное событие с вероятностью 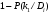 . .Если существует признак 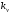 , встречающийся только при одном состоянии системы , встречающийся только при одном состоянии системы 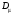 и не встречающийся при других, то он называется детерминированным. и не встречающийся при других, то он называется детерминированным.Из предыдущей формулы следует то, что при i= P(Di/k)=1, а при i P(Di/k)=0 Пример 1: Для обследуемого оборудование характерно три состояния: - состояние D1 – неисправности узла 1, наблюдаемые у 5% оборудования, т.е. P(D1)=0,05; - состояние D2 – неисправности узла 2, наблюдаемые у 15% оборудования, т.е. P(D2)=0,15; - нормальное состояние D3 – наблюдаемое у 80% оборудования, т.е. P(D3)=0,8. - Признак 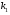 наблюдается при состоянии D1 в 20% случаев. Отсюда следует: наблюдается при состоянии D1 в 20% случаев. Отсюда следует:P(k1/D1)=0,2; при состоянии D2 в 40% будет P(k1/D2)=0,4 и при нормальном состоянии не наблюдается. - Признак k2 наблюдается при состоянии D1 в 30% случаев, 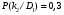 ; при состоянии ; при состоянии 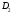 в 50% случаев, в 50% случаев, 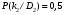 ; и при нормальном состоянии в 8% случаев, ; и при нормальном состоянии в 8% случаев, 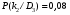 Условные вероятности состояний D1, D2, D3 по расчёту.
В первом случае с вероятностью 0,92 имеет место состояние 3, во втором случае с вероятностью 0,91— состояние 2, а в третьем случае вероятности второго и третьего состояния, близкие между собой. 1) 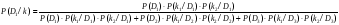 ; ;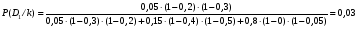 2) 2)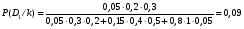 3) 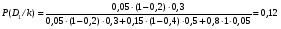 §5. Пути повышения надёжности ТО. 1. Повышение сопротивляемости ТО внешним воздействиям. Методы создания прочных, жёстких, износостойких узлов за счёт их рациональной конструкции. Применение виброзащитных схем. 2. Применение автоматики для повышения надёжности. Создание самонастраивающихся и саморегулируемых ТО, которые подобно живым организмам обладают функциями приспособления к изменившимся условиям работы и восстанавливают утраченную работоспособность, и это позволит ТО осуществлять свои функции длительное время. Автоматика так же необходима для обеспечения качества и надёжности ТО. 3. Создание ТО с регламентированными показателями надежности. Если сравнить две технические установки (для первой известны основные параметры и показатели, определяющие её надёжность, а для второй эти данные отсутствуют), то возможности по эффективному использованию этих установок различны. Информация о надёжности изделия имеет не меньшую ценность, чем достижения данного уровня качества. |
