Основы теории надёжности
 Скачать 0.92 Mb. Скачать 0.92 Mb.
|
Стохастическая природа изнашивания. - скорость изнашивания материала k – const, зависящая от материала и условий изнашивания (смазка, вакуум). Р – давление на поверхность трения V – скорость скольжения 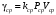 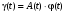 A(t) – случайная величина (t) – неслучайная величина Дисперсия процесса изнашивания.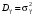 , ,где 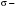 среднеквадратическое отклонение среднеквадратическое отклонениеДисперсия процесса изнашивания может быть подсчитана на основании теории о дисперсии независимых, не центрированных случайных величин. 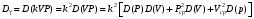 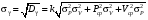 ГЛАВА 3. Модели формирования отказов. §1.Модель формирования постепенного отказа. 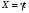 ; ;где X – толщина изношенного слоя, мкм; - скорость изнашивания, мкм/час; t – время работы механизма, час Скорость изнашивания подчиняется нормальному закону: 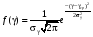 ; ; где 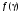 – плотность вероятности; – плотность вероятности; 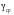 – среднее значение (мат. ожидание) скорости изнашивания; – среднее значение (мат. ожидание) скорости изнашивания; 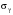 – среднеквадратическое отклонение скорости изнашивания. – среднеквадратическое отклонение скорости изнашивания.Предельно допустимое значение толщины изношенного слоя Xmax установлено из условия правильности функционирования изделия. При Х = Хmax наступает предельное состояние, которое и определяет срок службы (наработку) изделия до отказа. Это наступает в момент времени t = T (срок службы). Срок службы Т является функцией случайного аргумента , т.е. 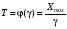 Средний срок службы изделия: 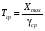 Задача заключается в отыскании плотности распределения 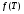 по заданной плотности распределения по заданной плотности распределения 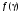 . . Для функции случайного аргумента в теории вероятности применяется формула: 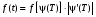 где (T) – функция, обратная функции (), т.е. если 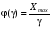 , то , то 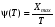 , , 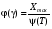 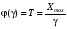 ; ;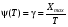 ; ;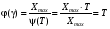 ; ;Итак, 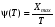 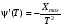 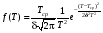 где 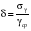 – коэффициент вариации, величина безразмерная – коэффициент вариации, величина безразмерная Для удобства расчётов введём безразмерное время 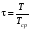 , тогда , тогда 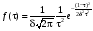 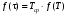 ; ; 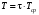 Для определения вероятности отказа F(T) необходимо проинтегрировать функцию плотности вероятности 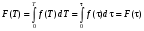 Если ввести переменную 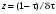 , данный интеграл сводится к функции Лапласа и, учитывая что вероятность безотказной работы , данный интеграл сводится к функции Лапласа и, учитывая что вероятность безотказной работы 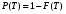 , получим , получим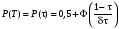 Зная, что 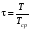 и и 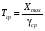 , получим , получим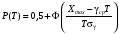 Подсчитаем вероятность F(): 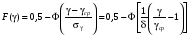 Из выражений 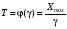 и и 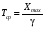 получаем получаем 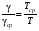 . . Тогда 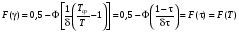 Т.е. 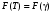 или или 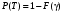 Параметр Х при заданном Т, так же как и скорость , распределен по нормальному закону с параметрами: 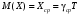 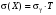 Поэтому вероятность безотказной работы численно равна площади под кривой плотности распределения f(X), заключённая от - до Xmax: 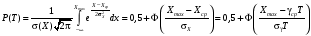 §2. Модель формирования постепенного отказа с учётом рассеивания начальных параметров. Более полная схема потери изделием работоспособности учитывает начальное рассеивание параметров изделия. 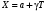 , ,где а – начальный параметр изделия, например, начальный зазор. Срок службы изделия является функцией двух независимых случайных аргументов a и . 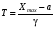 ; ; 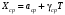 ; ; 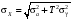 ; ; 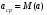 где 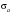 – среднеквадратическое отклонение случайного параметра – среднеквадратическое отклонение случайного параметра  Применяя условие, что 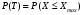 получаем: получаем: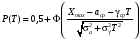 При 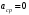 имеем имеем 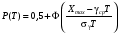 При 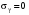 имеем имеем 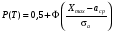 Последняя формула от времени 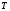 не зависит, т.е. это случай, когда не зависит, т.е. это случай, когда 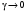 Пусть имеем Xmax и Xmin 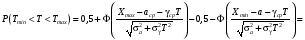 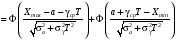 Если 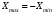 , a ср = 0, то , a ср = 0, то 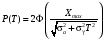 §3. Модели внезапных отказов.  Вероятность события В при условии выполнения события А: 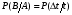 означает условную вероятность безотказной работы изделия за период времени t. означает условную вероятность безотказной работы изделия за период времени t.Применяя теорему умножения вероятностей для рассматриваемого случая, получим: 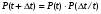 По определению, интенсивность отказов равна: 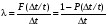 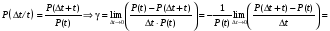 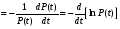 Откуда следует 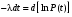 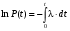 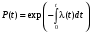 Эта формула выражает зависимость между вероятностью безотказной работы изделия и –характеристикой, которая в общем случае может быть функцией времени (t). Интенсивность отказов не является самостоятельной характеристикой, так как связана с P(t) и плотностью вероятности f(t): 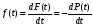 ; ;Поэтому 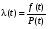 , т.к. , т.к. 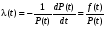 ; ;При = const: 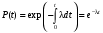 , , т.е. имеет место экспоненциальный закон Т.к. 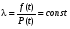 , то , то 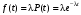 Средний срок службы (наработка) до отказа для экспоненциального закона будет: 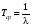 ; тогда ; тогда 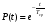 ; ;При 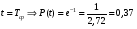 Т.е. при внезапных отказах после работы одинаковых деталей или узлов в течение времени 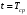 63% изделий откажут, а 37% — останутся работоспособными. 63% изделий откажут, а 37% — останутся работоспособными. Для современных деталей и узлов машин требуется высокая вероятность безотказной работы: P(t)=0,99  0,9999; 0,9999; Для значений P(t) > 0,9 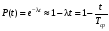 ГЛАВА 4. Надёжность в период постепенных отказов. §1.Нормальное распределение. Для постепенных отказов нужны законы распределения времени безотказной работы, которые дают в начале низкую плотность распределения, затем максимум и далее падение, связанное с уменьшением числа работоспособных элементов. Нормальное распределение является наиболее универсальным, удобным и широко применяемым для практических расчётов.   Нормальному распределению подчиняется наработка до отказа многих восстанавливаемых и невосстанавливаемых изделий, размеры и ошибки измерения деталей и т.д. Плотность распределения: 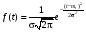 Распределение содержит два независимых параметра: 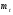 – математическое ожидание – математическое ожидание - среднеквадратическое отклонение Значения этих параметров оцениваются по результатам испытаний: 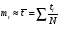 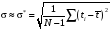 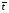 , * - оценки математического ожидания и среднеквадратического отклонения. , * - оценки математического ожидания и среднеквадратического отклонения.Функция распределения: 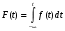 Вероятность отказа и вероятность безотказной работы соответственно равны: 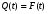 ; ; 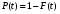 ; ; 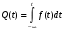 ; ; 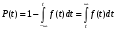 Вычисление интегралов заменяют использованием таблиц. Для использования таблиц применяют следующую подстановку: 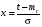 х – квантиль нормированного нормального распределения. Величину X обозначаем up. Часто в литературе по теории надёжности вместо интегральной функции распределения F(x) используют функцию Лапласа: 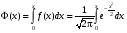 Очевидно, что 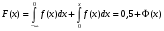 Вероятность отказа и вероятность безотказной работы, выраженные через функцию Лапласа, отличаются пределами интегрирования: 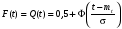  Помимо задачи оценки вероятности безотказной работы за данное время или за данную наработку встречается обратная задача: определение времени или наработки, соответствующих заданной вероятности безотказной работы. Значение этой наработки (времени) определяют с помощью квантилей нормированного нормального распределения. 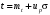 Отношение 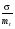 называют коэффициентом вариации называют коэффициентом вариации 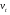 ЗАДАЧА 1 Оценить вероятность безотказной работы в течение времени 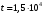 часов изношенного подвижного сопряжения, если ресурс по износу подчиняется нормальному распределению, часов изношенного подвижного сопряжения, если ресурс по износу подчиняется нормальному распределению, 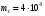 часов и = 10 часов. часов и = 10 часов.РЕШЕНИЕ: Находим квантиль  По таблице квантилей определяем нормальное распределение P(t) = 0,9938. ЗАДАЧА 2 Оценить 80% ресурса ТО, если известно, что его долговечность ограничена по износу, ресурс подчиняется нормальному распределению с параметрами: 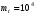 часов, часов, 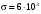 часа. часа.РЕШЕНИЕ: при P(t) = 0,8 по таблице находим 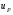 = - 0,84 и = - 0,84 и  часа часа§2 Усечённое нормальное распределение. Получается из нормального при ограничении интервала изменения случайной величины при том условии, что площадь под кривой должна оставаться равной единице. При этом график нормального распределения «приподнимается»: 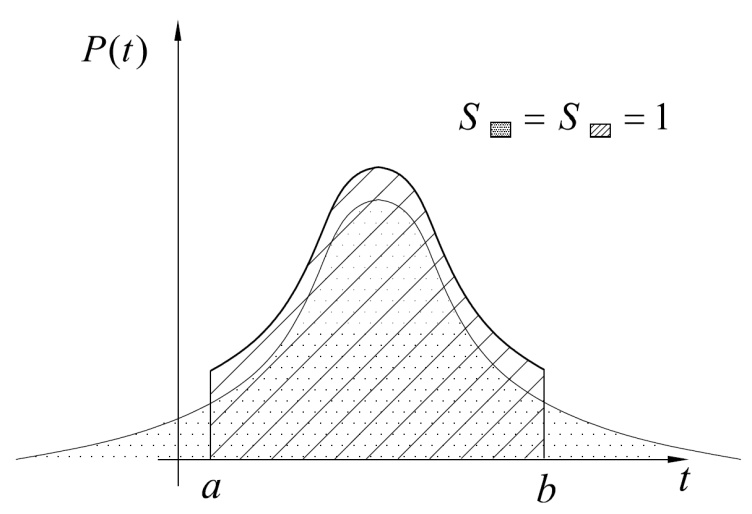 Плотность распределения записывается также, как и плотность нормального распределения, но с коэффициентом пропорциональности С: 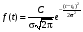 где 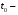 значение случайной величины, соответствующей максимуму f(t) и называемое модой. значение случайной величины, соответствующей максимуму f(t) и называемое модой.Коэффициент С для распределения, ограниченного пределами изменения от a до b определяется из условия: 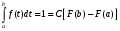 где 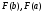 – значения функции нормального распределения для предельных значений t. Отсюда – значения функции нормального распределения для предельных значений t. Отсюда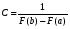 §3.Логарифмические нормальные распределения. Логарифм случайной величины распределяется по нормальному закону. Как распределение положительных величин, оно несколько точнее, чем нормальное, описывает наработку до отказа деталей, в частности, по усталости. Его успешно применяют для описания наработки подшипников качения, электронных ламп и других изделий. Плотность распределения описывается зависимостью 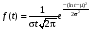 где и - параметры, оцениваемые по результатам испытания. При испытаниях N изделий до отказа 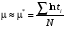 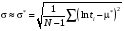 где *,* - оценка параметров и . Вероятность безотказной работы можно определить по таблицам для нормального распределения в зависимости от значения квантили. 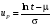 Математическое ожидание наработки до отказа: 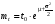 Среднеквадратическое отклонение: 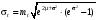 ; ;Коэффициент вариации: 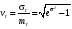 Часто применяют запись зависимости для логарифмического нормального распределения в десятичных логарифмах. Соответственно плотность распределения: 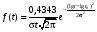 Оценки параметров 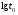 и определяются по результатам испытаний. и определяются по результатам испытаний.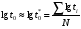 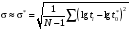 где 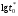 и и 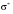 — оценки параметров — оценки параметров 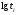 и и . .Математическое ожидание 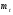 , среднеквадратическое отклонение , среднеквадратическое отклонение 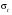 и коэффициент вариации и коэффициент вариации 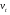 наработки до отказа соответственно равны: наработки до отказа соответственно равны: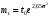 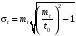 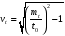 §4. Математические ожидания, мода и медиана непрерывной случайной величины.  Математическое ожидание (m) непрерывной случайной величины – это абсцисса центра тяжести фигуры, расположенной под кривой распределения. Мода непрерывной случайной величины (M) – это наиболее вероятное значение случайной величины или max кривой распределения. Медиана непр=ерывной случайной величины (Me) – это абсцисса точки, в которой площадь, ограниченная кривой распределения, делится пополам. Примечание: В случае симметрии нормального распределения медиана совпадает с модой и математическим ожиданием.  |
