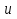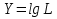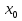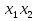Основы теории надёжности
 Скачать 0.92 Mb. Скачать 0.92 Mb.
|
|
§5. Статистический анализ результатов испытаний. Статистический анализ результатов испытаний необходим для оценки достоверности эксперимента и включает следующие этапы: 1. Проверка воспроизводимости или постоянства дисперсии отклика сводится к проверке гипотезы об однородности дисперсий 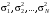 , найденных по результатам N опытов. , найденных по результатам N опытов.Дисперсия отклика 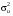 для u-го опыта равна: для u-го опыта равна: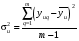 , u = 1,2,…N , u = 1,2,…Nгде yuq – отклик u-го опыта при q-м повторе, m – число повторов опыта. Вычисляем экспериментальные значения критерия Кохрена, т.е. отношение максимальной 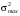 из N дисперсий к сумме всех дисперсий: из N дисперсий к сумме всех дисперсий: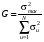 где G≤ G табл – соответствие выполненного условия однородности дисперсий. Гипотеза об однородности дисперсий подтверждается, если вычисленное значение критерия не превышает критического значения, определённого по соответствующим таблицам, в зависимости от числа степеней свободы k1 = m – 1; k2 = N и доверительной вероятности 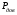 . .2. Адекватность модели, т.е. пригодность ранее принятой функции отклика для описания реального объекта исследования, проверяют по отношению дисперсий адекватности и воспроизводимости. Дисперсию воспроизводимости или оценку дисперсии отклика определяют по формуле 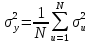 Дисперсию адекватности определяем по формуле: 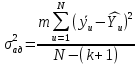 , , Где k – число факторов; 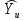 - расчетная оценка среднего значения отклика в u-м опыте, вычисляемая по соответствующему полиному. - расчетная оценка среднего значения отклика в u-м опыте, вычисляемая по соответствующему полиному. Например, для линейной модели 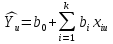 Где 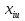 - значение i-го фактора в u-м опыте. - значение i-го фактора в u-м опыте.Экспериментальное значение F-критерия (критерия Фишера) равно 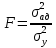 Модель считают адекватной, если вычисленное значение F меньше критического, определённого по таблицам F-распределения [5, 45], в зависимости от числа степеней свободы 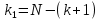 , ,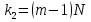 и доверительной вероятности и доверительной вероятности 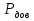 . .Для насыщенных планов, в которых число определяемых коэффициентов равно числу опытов, для проверки адекватности проводят дополнительные опыты. Так, для линейной модели дополнительно ставят опыты в центре плана. По расхождению между полученным и расчетным значениями отклика принимают решения об адекватности модели. При неадекватности модели возможны следующие действия: усложнение модели, достройка плана, преобразование переменных, изменение интервалов варьирования. 3. Значимость коэффициентов модели проверяем поt-критерию Стьюдента. Проверку начинаем с вычисления дисперсий коэффициентов. Для планов дробного и полного факторного эксперимента типа 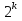 дисперсии оценок коэффициентов дисперсии оценок коэффициентов 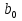 , , 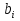 , , 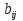 одинаковы и определяются по формуле одинаковы и определяются по формуле 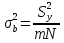 . .Экспериментальное значение критерия Стьюдента равно 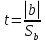 , ,Где 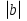 - абсолютное значение оценки проверяемого коэффициента, т.е. одного из коэффициентов - абсолютное значение оценки проверяемого коэффициента, т.е. одного из коэффициентов 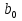 , , 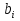 , , 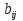 . .Коэффициент считают значимым, если вычисленное значение критерия больше, чем критическое значение, выбираемое по таблицам распределения Стьюдента , в зависимости от числа степеней свободы 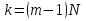 и доверительной вероятности и доверительной вероятности 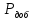 . .Для квадратичной модели, когда испытания проводят по ортогональному центральному плану, дисперсии оценок коэффициентов модели определяют по следующим зависимостям: 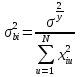 , , 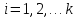 . . , , 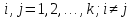 ; ;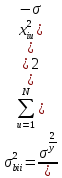 , , 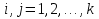 ; ;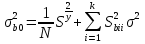 , ,Где 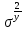 - общая дисперсия среднего значения отклика определяется по формуле - общая дисперсия среднего значения отклика определяется по формуле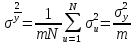 . .Далее для каждого из коэффициентов вычисляется t-критерий Стьюдента (отношение абсолютного значения коэффициента к его среднему квадратичному отклонению) и сравнивают с табличным значением, найденного в зависимости от числа степеней свободы 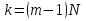 и доверительной вероятности и доверительной вероятности 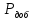 . .Пример. Исследовать влияние радиального 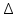 и углового и углового 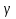 смещений осей соединяемых валов на долговечность муфты с резиновым торообразным элементом вогнутого профиля. Муфта нагружена номинальным моментом Т= 100 Нм, наружный диаметр муфты смещений осей соединяемых валов на долговечность муфты с резиновым торообразным элементом вогнутого профиля. Муфта нагружена номинальным моментом Т= 100 Нм, наружный диаметр муфты 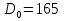 мм. мм.Решение: Схематизация эксперимента. На муфту (объект исследования) действуют два фактора: радиальное 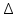 и угловое и угловое 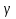 смещения полумуфт. Кодированные значения факторов обозначаем соответственно через смещения полумуфт. Кодированные значения факторов обозначаем соответственно через 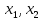 и определяем по следующим зависимостям: и определяем по следующим зависимостям: 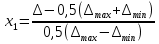 ; ; 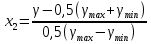 . .Предельные значения радиальных и угловых смещений устанавливаем, исходя из опыта эксплуатации муфт: 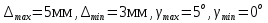 . Подставляя предельные значения в формулу для . Подставляя предельные значения в формулу для 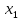 и и 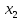 , получаем , получаем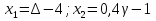 . .В качестве отклика Y рассматриваем логарифмы ресурса 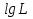 , где L-ресурс, выраженный в оборотах муфты. , где L-ресурс, выраженный в оборотах муфты.Требуется оценить функцию отклика, т.е. найти связь между факторами и откликом. Функцию отклика задаем полиномом первого порядка с учетом эффекта взаимодействия 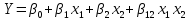 , ,Где 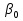 , ,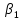 , , 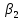 , , 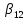 - коэффициенты функции. - коэффициенты функции.Соответственно оценку функций отклика (эмпирического уравнения регрессии) ищем в виде 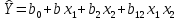 , ,Где 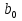 , ,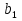 , , 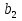 , , 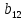 - оценки коэффициентов - оценки коэффициентов 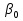 , ,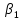 , , 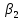 , , 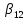 соответственно. соответственно.При планировании эксперимента выбран план полного факторного эксперимента типа 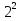 . Число опытов . Число опытов 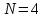 ;число повторов каждого опыта ;число повторов каждого опыта 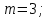 необходимое число образцов равно необходимое число образцов равно 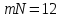 . .Испытания проводятся на стенде с замкнутым контуром, спроектированном и изготовленном в МВТУ им. Н. Э. Баумана. Циркулирующий в контуре момент соответствовал номинальному моменту испытуемой муфты. Конструкция стенда позволяет изменять радиальное и угловое смещение полумуфт в широких пределах. Результаты испытаний на долговечность представлены в виде значений логарифмов ресурса.
Учитывая, что число повторов m=3, среднее значение 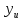 и среднее квадратичное отклонение и среднее квадратичное отклонение 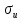 логарифмы ресурса в -м опыте, определяем по формулам логарифмы ресурса в -м опыте, определяем по формулам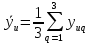 ; ; 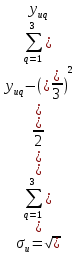 Где 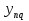 - текущее значение логарифма ресурса. - текущее значение логарифма ресурса.По результатам испытаний определяем оценки коэффициентов функций отклика 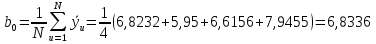 ; ;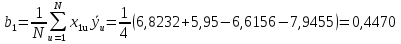 ; ;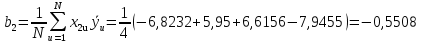 ; ;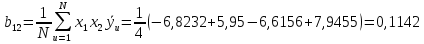 . .Оценка функции отклика в кодированных значениях факторов записываем в виде 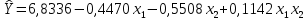 . .После подставки значений 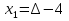 и и 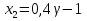 получаем оценку зависимости среднего значения логарифма ресурса от радиальных и угловых смещений осей соединяемых валов получаем оценку зависимости среднего значения логарифма ресурса от радиальных и угловых смещений осей соединяемых валов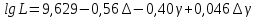 . .Статистический анализ результатов испытаний начинаем с проверки однородности дисперсии. Вычисляем критерий Кохрена 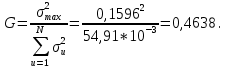 Критическое значение критерия 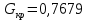 выбрано [45] в зависимости от числа степеней свободы выбрано [45] в зависимости от числа степеней свободы 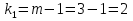 , , 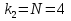 и доверительной вероятности и доверительной вероятности 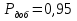 . .Критическое значение критерия 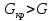 , что соответствует выполнению условия однородности дисперсий. , что соответствует выполнению условия однородности дисперсий.Для проверки значимости коэффициентов модели вычисляем дисперсию воспроизводимости 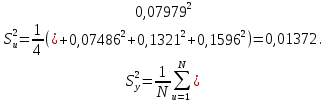 Дисперсия коэффициентов модели 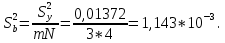 Экспериментальные значения критерия Стьюдента 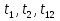 для коэффициентов для коэффициентов 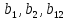 соответственно равны: соответственно равны: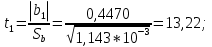 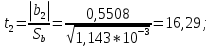 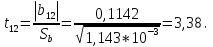 Критическое значение критерия 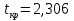 выбрано по [5.45] в зависимости от числа степеней свободы выбрано по [5.45] в зависимости от числа степеней свободы 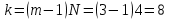 и доверительной вероятности и доверительной вероятности 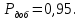 Так как значения критерия 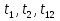 больше критического значения больше критического значения 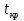 , полагают, что все коэффициенты модели значимы. Следовательно, ранее определенная зависимости среднего значения логарифма ресурса от радиального , полагают, что все коэффициенты модели значимы. Следовательно, ранее определенная зависимости среднего значения логарифма ресурса от радиального 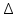 и углового и углового 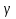 смещений остается в силе. смещений остается в силе. | |||||||||||||||||||||||||||||||||||||||||||||||