лекции по эконометрике. Основные понятия и определения эконометрики
 Скачать 0.78 Mb. Скачать 0.78 Mb.
|
4. СТАТИСТИЧЕСКИЕ СВОЙСТВА ОЦЕНОК КОЭФФИЦИЕНТОВМЛРМ. Полученные оценки неизвестных коэффициентов регрессионного уравнения Для того чтобы оценки, полученные по МНК, давали «наилучшие» результаты, мы потребуем от остаточного члена или ошибки и от X выполнения следующих условий (предположения относительно того, как генерируются наблюдения):
В матричной форме: 1-5 - КЛРМ, 1-6 - НЛРМ, условия 1-6 - условия Гаусса-Маркова. В случае НЛРМ условие 5. эквивалентно условию статистической независимости ошибок для разных наблюдений. Действительно, если две нормально распределенные величины не коррелированны, то они независимы. Обсудим эти условия.
Это условие состоит в том, что математическое ожидание случайного члена равно нулю в любом наблюдении. Иногда случайный член бывает положительным, иногда отрицательным, но он не должен иметь смещения ни в одном возможном направлении. Надо сказать, что если в уравнение включается постоянный член, то бывает разумным предположить, что первое условие выполняется автоматически, т. к. роль константы и состоит в определении любой систематической составляющей в Y, которую не учитывают объясняющие переменные (если спецификация модели выбрана правильно). Иллюстрация: предположим, что Таким образом, исходная модель эквивалентна новой модели с ошибкой, имеющей нулевое математическое ожидание и другим свободным членом. 4. Второе условие говорит нам о том, что дисперсии ошибок постоянны для всех наблюдений. Иногда случайный член будет больше, иногда меньше, иногда больше, но не должно быть априорной причины для того, чтобы он порождал большую ошибку в одних наблюдениях, чем в других. Условие независимости ошибок от номера наблюдения называют гомоскедастичностью. Случай, когда условие гомоскедастичности нарушается, называется гетероскедастичностью. Этот случай можно иногда наблюдать графически: Рисунок 1. рисунок про гомо и гетероскедастичность. 5. Условие указывает на некоррелированность ошибок для разных наблюдений. Условие предполагает отсутствие систематической связи между значениями случайного члена в любых двух наблюдениях. Это условие почти всегда нарушается, если наши данные представляют собой временные ряды. В случае если это условие не выполняется, говорят об автокорреляции остатков. Для простейшего случая Рисунок 2. рисунок про > 0 и < 0 6. Это предположение не является чем-то сверхъестественным и высосанным из теоретического пальца. Действительно, как мы отмечали на прошлом занятии, i включает в себя много факторов, которые, в принципе, можно считать независимыми. Отсюда, как следует из центральной предельной теоремы Ляпунова, i будут иметь почти нормальное распределение. Отметим, что в случае КЛРМ условие 6 эквивалентно условию статистической независимости ошибок для разных наблюдений. Действительно, если две нормально распределенные величины не коррелированны, то они независимы. В общем случае это не выполняется. А поскольку они независимы, то вектор ошибок имеет множественное нормальное распределение или величины i будут иметь совместное нормальное распределение с вектором средних 0 и ковариационной матрицы Итак, мы с вами находимся в условиях КЛРМ. Посмотрим, какими свойствами обладают в этом случае наши оценки Желаемые свойства оценок следующие несмещенность, эффективность, состоятельность. По имеющейся выборке мы можем построить несколько оценок одного и того же параметра. Нас будут интересовать не все возможные оценки, а лишь оценки, обладающие определенными свойствами. Вот эти свойства:
Как правило, эконометристов более интересует состоятельность оценки, чем ее Несмещенность. Смещенная, но состоятельная оценка может не равняться истинному значению в среднем, но с ростом выборки будет приближаться к истинному значению параметра. Пример несмещенной, но неэффективной оценкой и смещенной, но эффективной на рисунке. Свойства (с доказательствами для парного случая: Свойство 1. Линейная зависимость оценок от наблюдаемых значений Y. поскольку Легко убедится, что Аналогично преобразовывая выражение для Свойство 2. Для доказательства мы использовали 2 и 3. Свойство 3. Матрица ковариаций оценок: 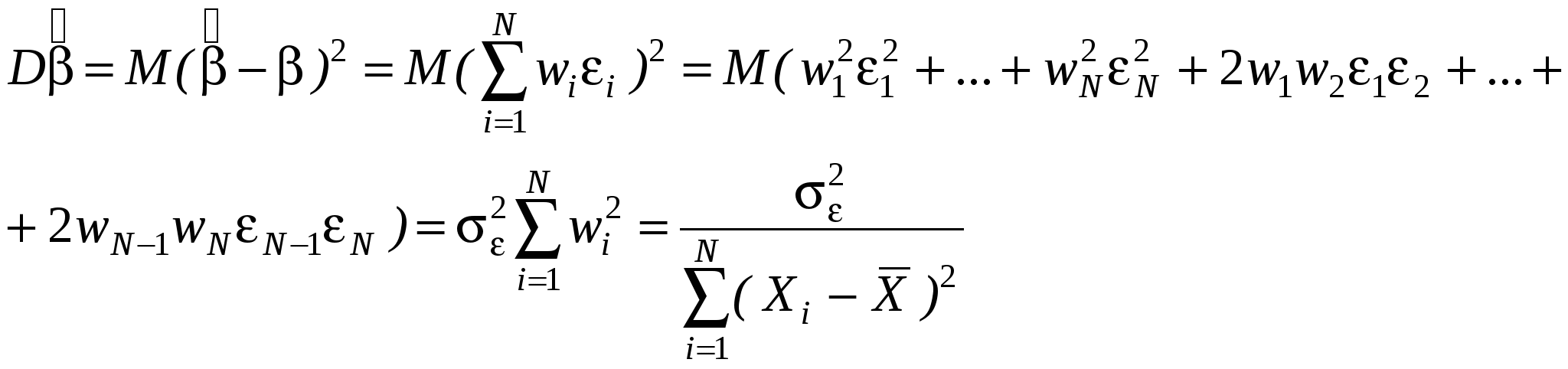 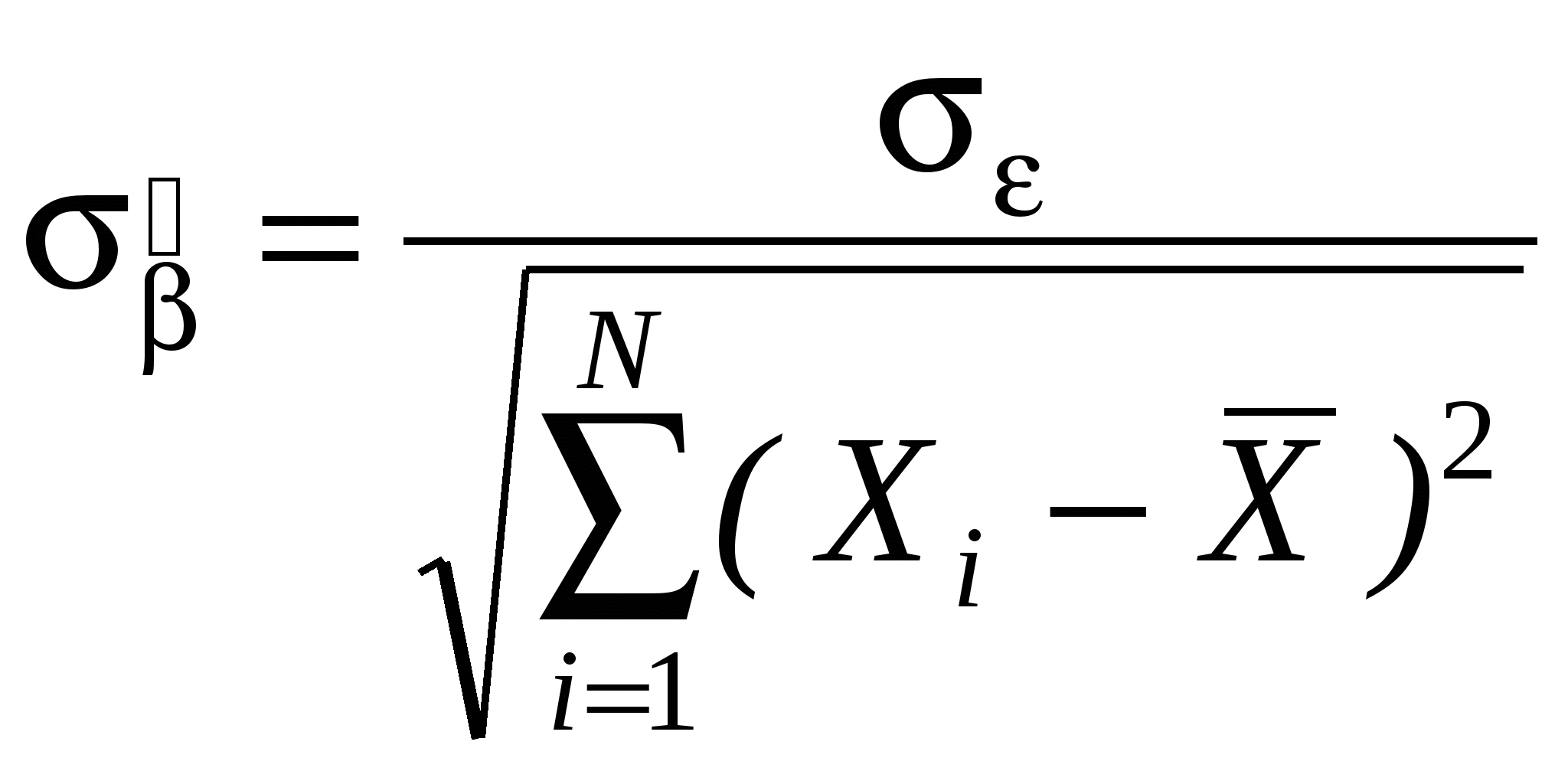 . .Аналогично выводится формула для . 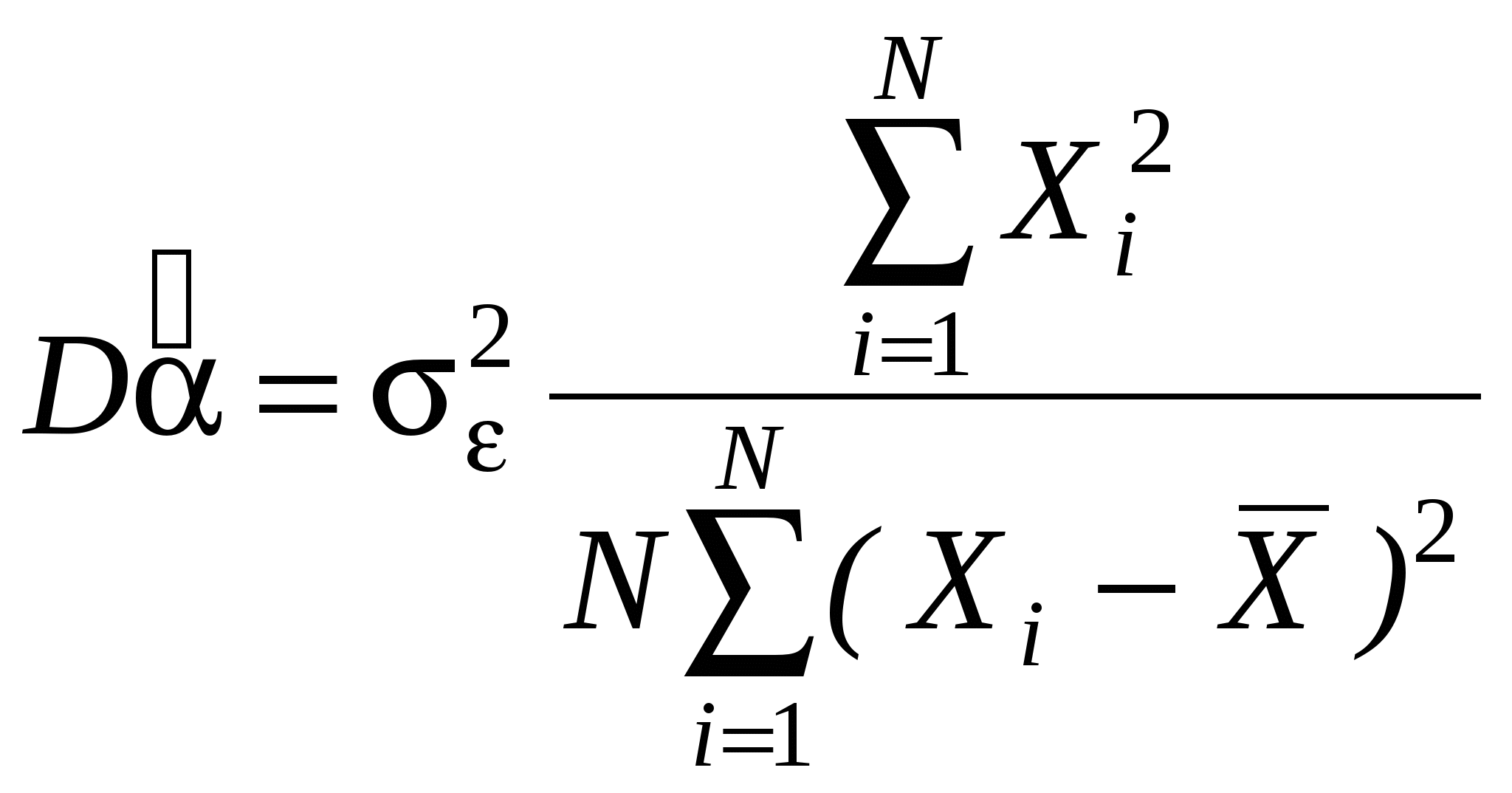 Подобным образом можно отыскать ковариацию: 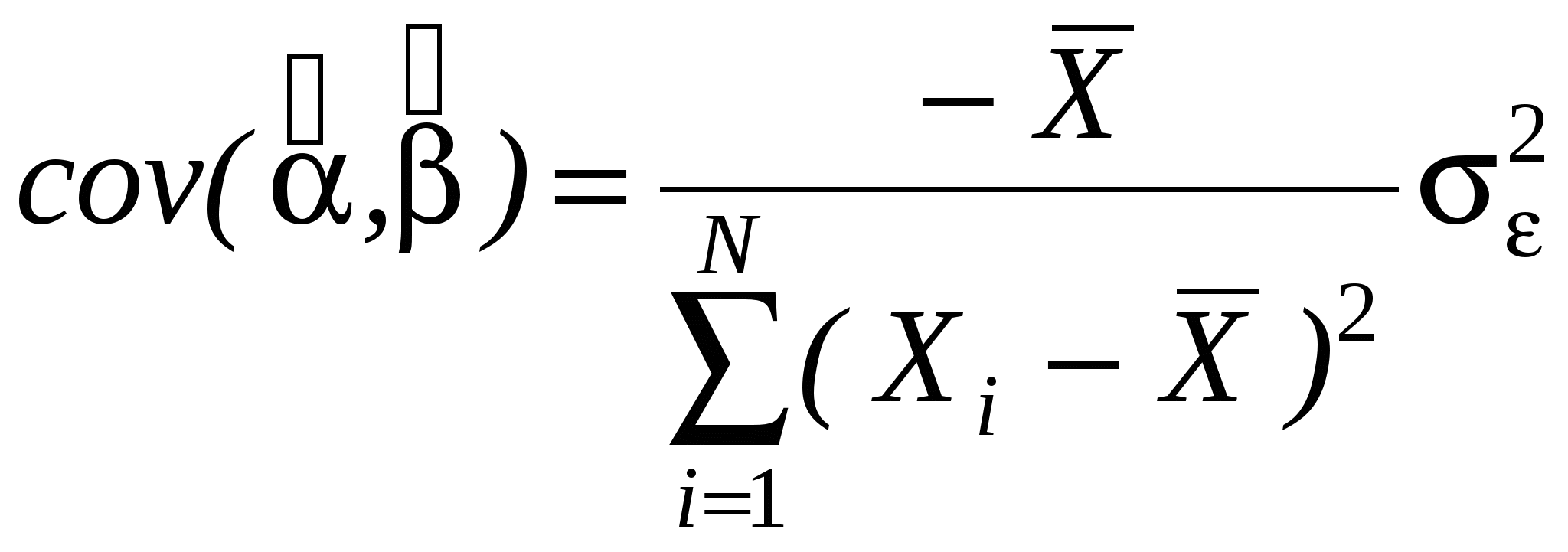 . .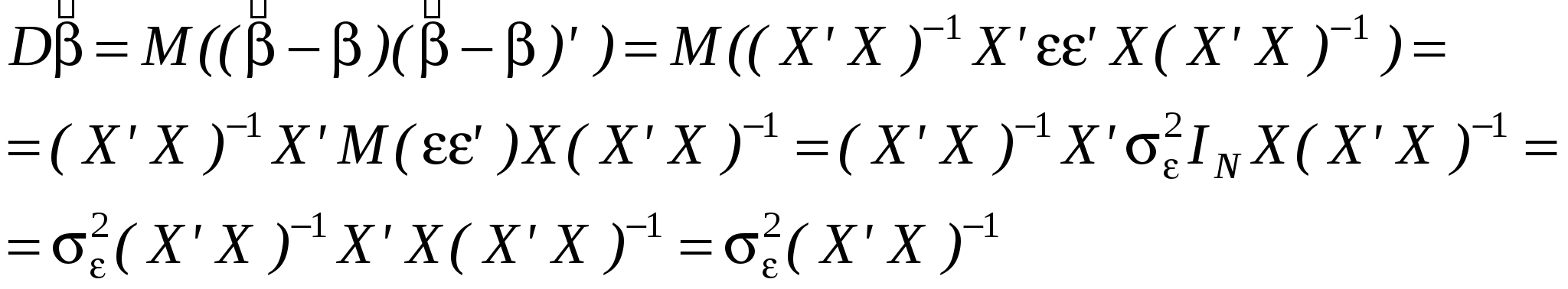 (пользовались тем, что матрица, обратная к симметричной, так же симметричная) посмотреть, что еще здесь надо пользовались 3, 4 и 5. Свойство 4. Теорема Гаусса-Маркова. В условиях 1-5 МНК-оценки МЛРМ представляют собой наилучшие линейные несмещенные оценки, т. е. в классе линейных несмещенных оценок МНК-оценки обладают наименьшей дисперсией. Best Linear Unbaised Estimation (BLUE) Важность теоремы Гаусса-Маркова. Мы можем придумать много оценок возможных для коэффициентов , в частности, можем придумать много линейных оценок, т. е. таких оценок, которые выражаются в виде взвешенного среднего наблюдений объясняемой переменной. Некоторые из этих оценок могут быть несмещенными как, например, «наивная» оценка. Так вот, оценки коэффициентов уравнения по методу наименьших квадратов в случае классической парной модели – это наилучшие оценки в том смысле, что среди всех возможных линейных несмещенных оценок эти оценки имеют наименьшую дисперсию. BestLinearUnbiasedEstimator – BLUE Вопрос нахождения такой оценки будет возникать в нашем курсе снова и снова, т. к. мы увидим, что при нарушении условий Гаусса-Маркова МНК-оценки уже не будут «BLUE». В этом случае наша цель будет заключатся в построении других оценок, не МНК, которые уже будут «BLUR». Обратите внимание, что в выражении матрицы ковариаций Свойство 5. 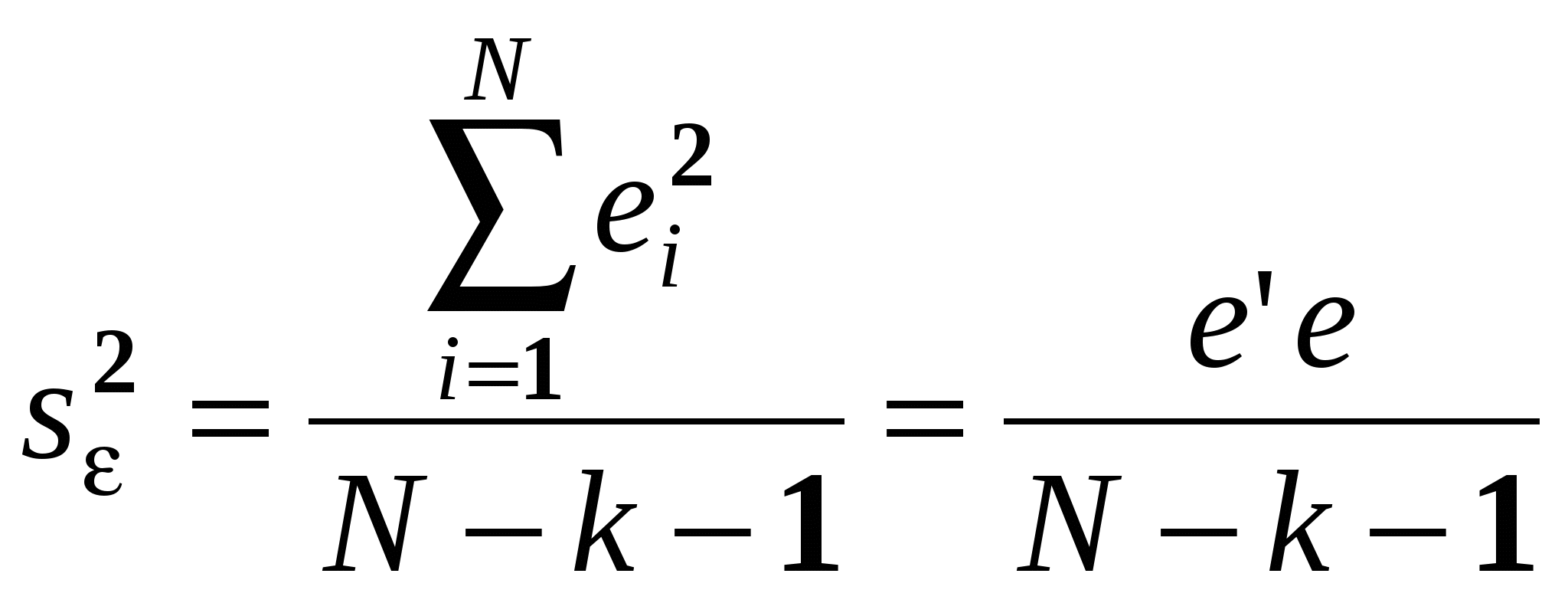 - несмещенная оценка - несмещенная оценка Итак, оценка Для парной модели 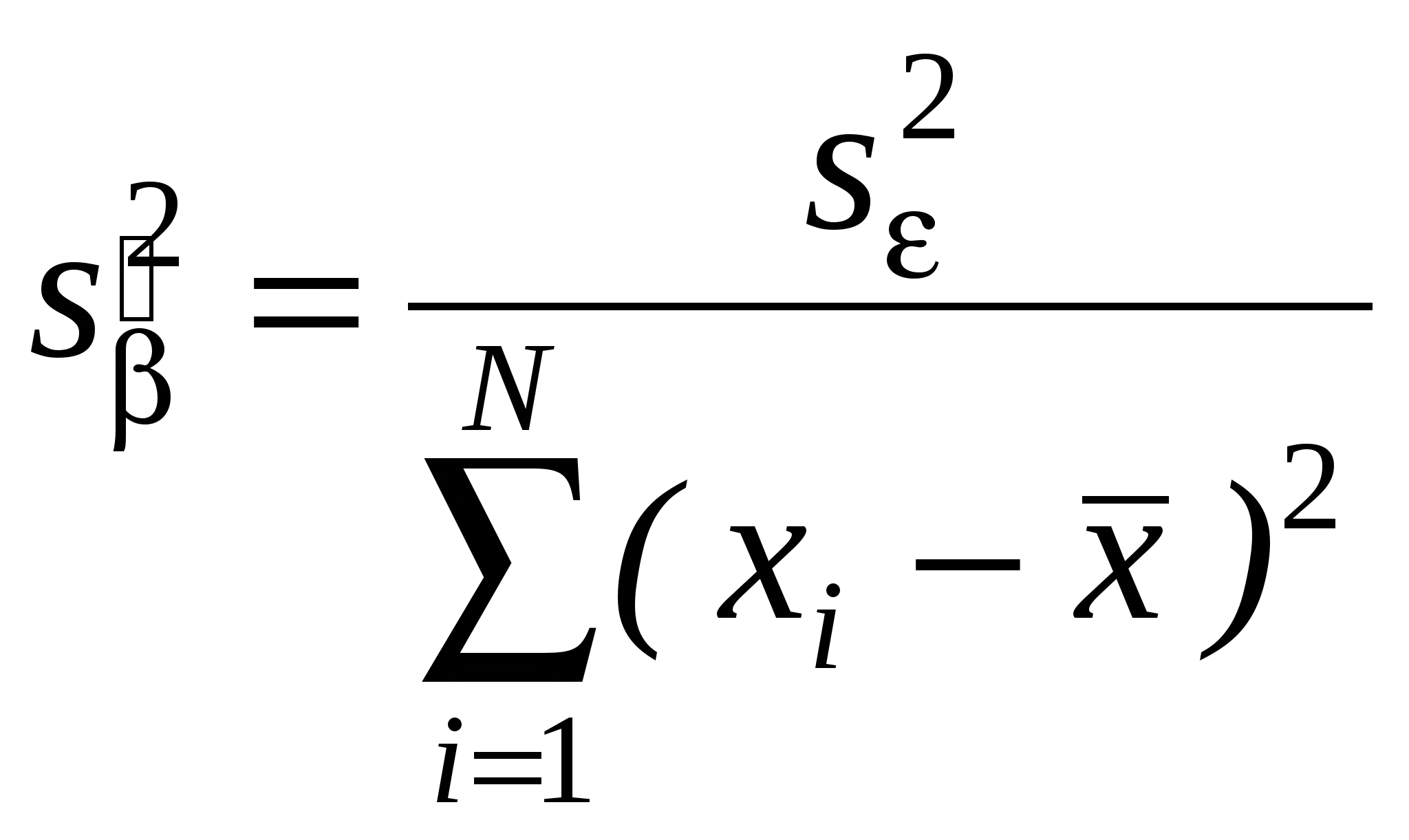 , , 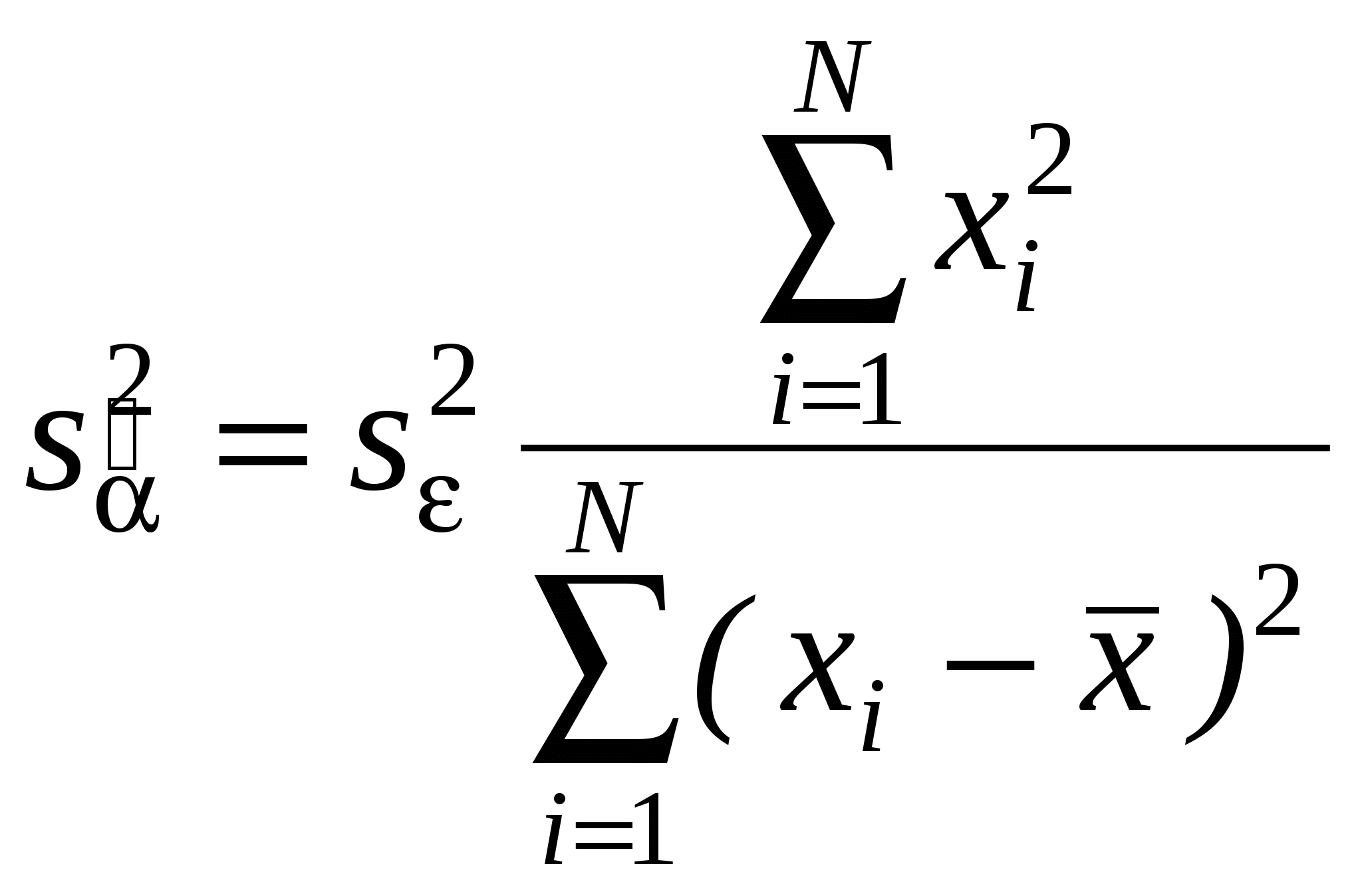 Стандартные отклонения коэффициентов регрессии, вычисленные на основе предыдущей формулы, приводятся в результатах регрессии практически во всех статистических пакетах. До сих пор мы нигде не использовали свойство 6, т. е. не делали никаких предположений о распределении вероятностей ошибок i. Что будет, если мы запостулируем нормальную форму этого распределения. Свойство 6. В предположениях НЛРМ Свойство 7. В случае НРЛМ 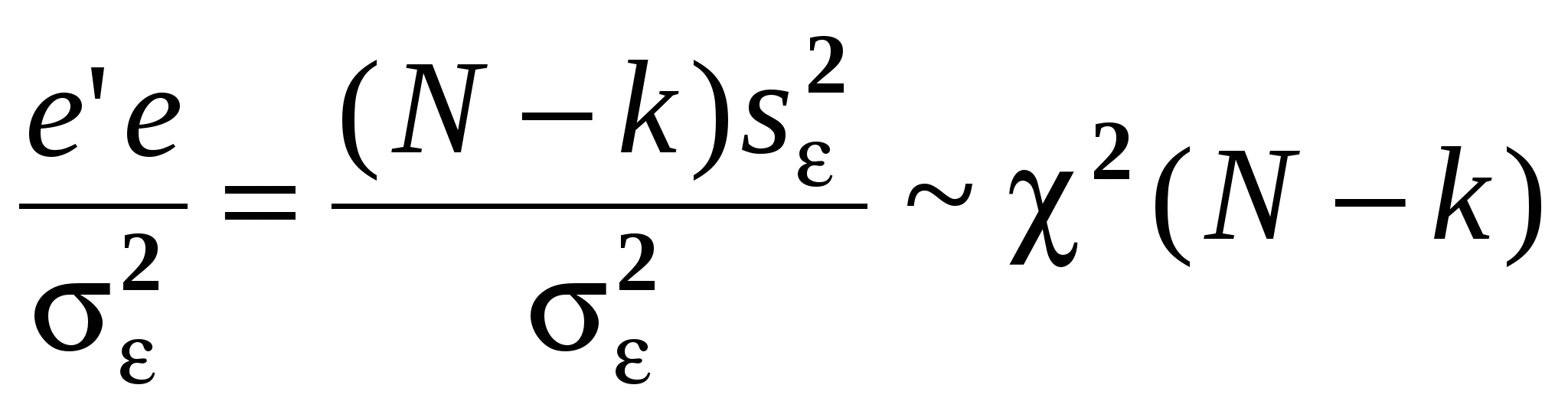 - без доказательства. - без доказательства.Свойство 8. В условиях НЛРМ оценки ПРОВЕРКА ГИПОТЕЗ ОТНОСИТЕЛЬНО КОЭФФИЦИЕНТОВ РЕГРЕССИИ. Предположим, что мы находимся в условиях НМЛРМ. 1. H0: = 0, или учитывая, что H0: M Поскольку 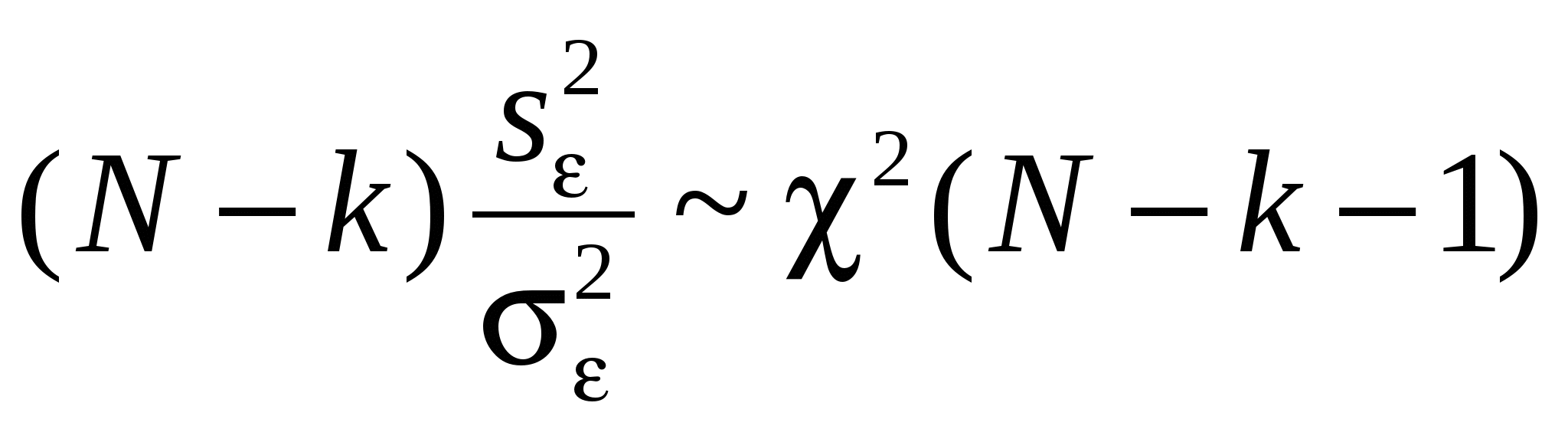 и оценки и оценки 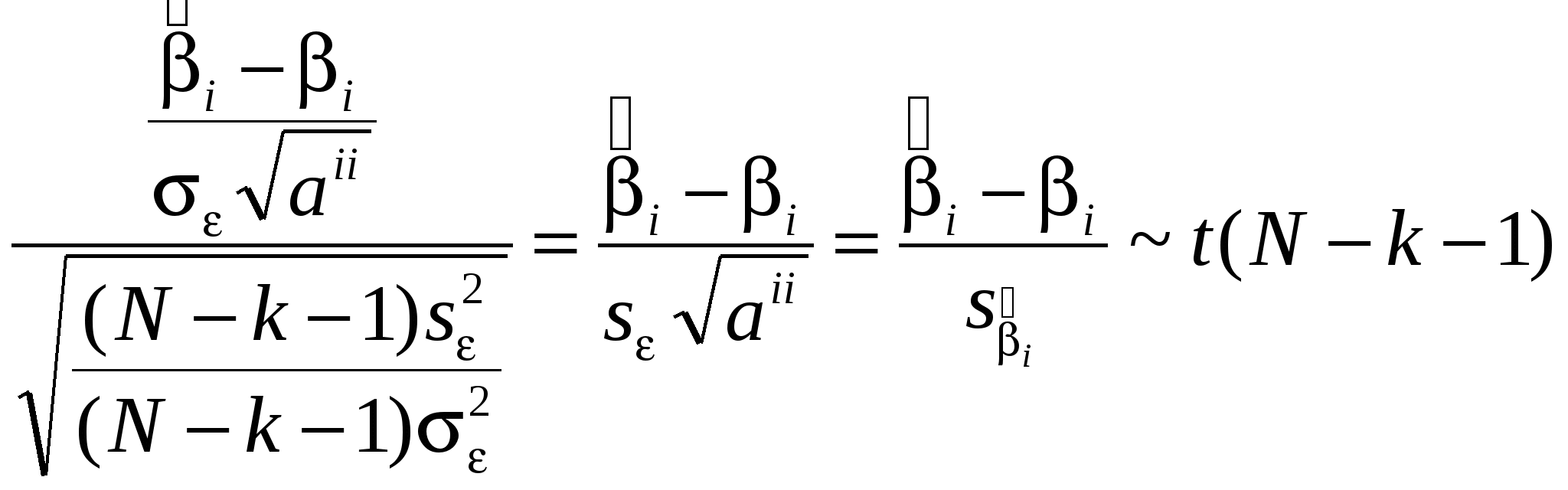 . .Вычисляем наблюдаемое значение критерия tнабл/. Для проверки нулевой гипотезы при различных альтернативных гипотезах: Hа: i i0. tкр находим из таблиц критических точек распределения Стьюдента с N-k-1 степенями свободы для выбранного уровня значимости и учитывая, что критическая область двусторонняя - Если же у нас критерий односторонний, то все сохраняется, за исключением критического значения статистики. Его мы ищем по таблицам критических точек распределения Стьюдента с N-k-1 степенями свободы для выбранного уровня значимости и учитывая, что критическая область односторонняя - Особенно просто критерий выглядит в случае, когда i0 = 0, т. е. в случае, когда мы хотим убедиться в значимости этого коэффициента и таким образом убедиться в наличии связи между Y и Xi: Если мы теперь рассмотрим неравенство Разрешим это неравенство относительно : Не говорят, что доверительный интервал содержит с вероятностью содержит истинное значение параметра . Поскольку истинное значение параметра существует независимо от нас, а доверительный интервал мы строим, т. о. не попадает в доверительный интервал, а доверительный интервал с той или иной вероятностью попадает на .
Пусть константа включена в число регрессоров. Процедура разделения вариации переменной Y на две составляющие позволяет провести нам тест на существование линейной зависимости между переменной Y и переменными X1,…,Xk. Н0: Таким образом, справедливость нулевой гипотезы означает, что ни одна из переменных X1,…,Xkне помогает нам объяснить вариацию Y. Эта гипотеза позволяет нам судить о значимости регрессии в целом. Эта гипотеза об отсутствии линейной связи между Y и X1,…,Xk. Проверка нулевой гипотезы осуществляется при помощи следующего критерия: При справедливости нулевой гипотезы данная статистика имеет распределение Фишера с числом степеней свободы числителя k и знаменателя N-k-1. Если нулевая гипотеза верна, то следует ожидать, что RSS, R2 и, следовательно, F, близки к нулю. Таким образом, если значение F-статистики велико, мы нулевую гипотезу отвергаем. Граничное значение, начиная с которого мы отвергаем гипотезу, находится из таблиц распределения Фишера для выбранного уровня значимости и числу степеней свободы числителя k и знаменателя N-k-1 - Итак, при помощи F-статистики мы проверяем значимость коэффициента детерминации. Если F-статистика незначимо отличается от нуля, это означает, что объясняющие переменные, участвующие в модели на самом деле не очень-то нам помогают объяснит вариацию переменной Y. Для парного случая F – статистика выглядит следующим образом: 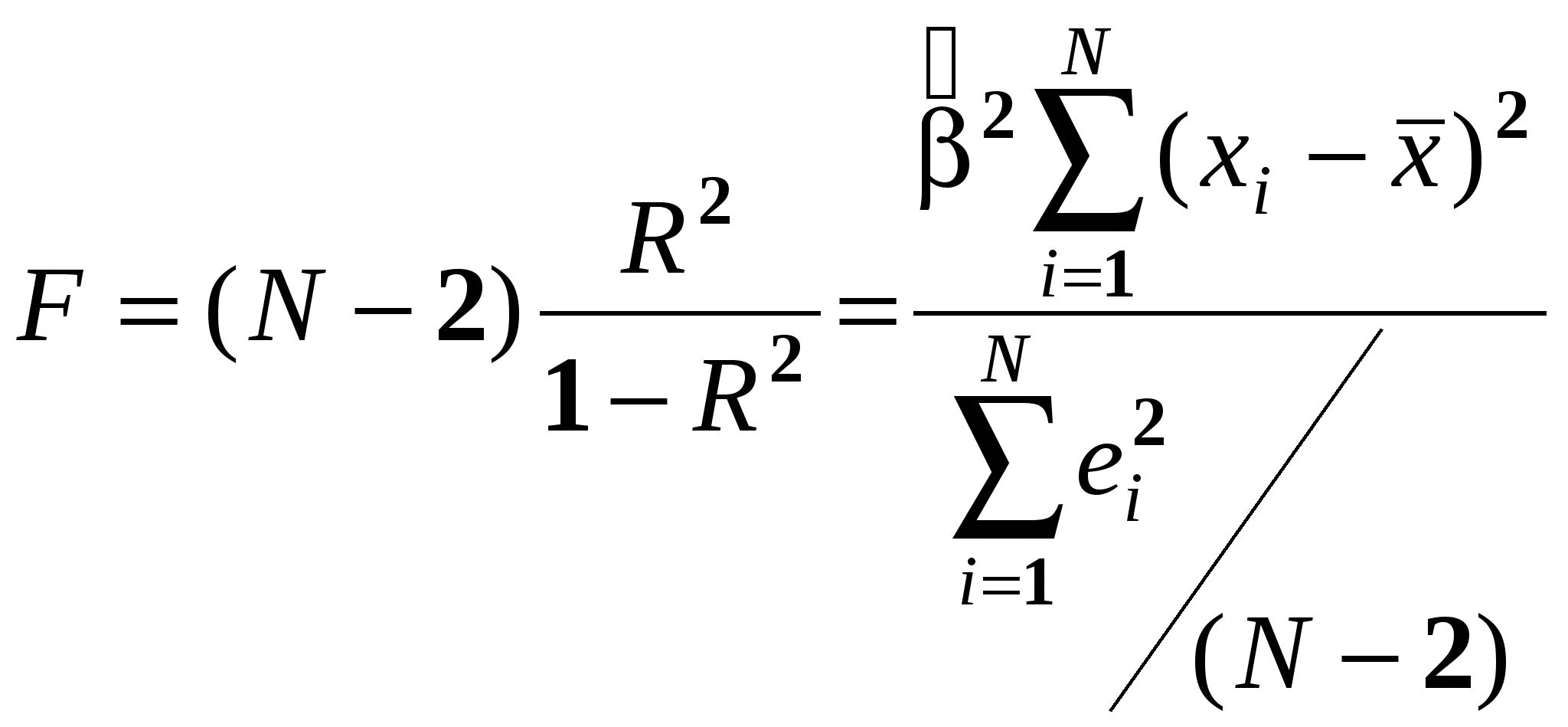 - Упражнение - УпражнениеСравнивая предыдущее выражение и выражение для t-статистики коэффициента наклона, получим, что F= t2: 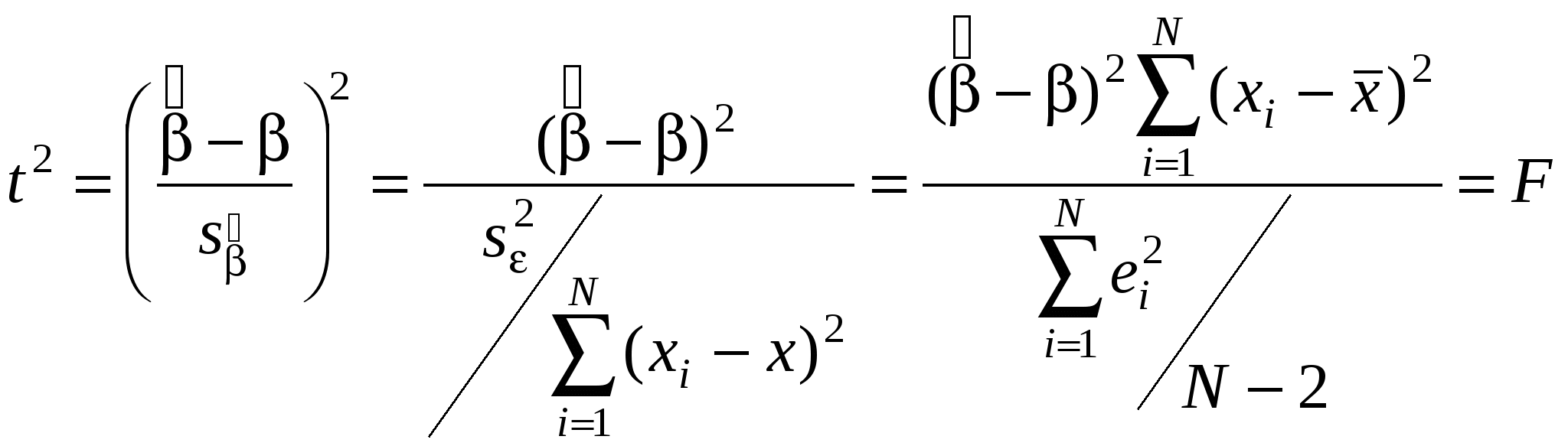 . .Таким образом, проверка гипотезы Н0: = 0 , используя F и t-статистики, дает для одномерной регрессионной модели дает тождественные результаты. 3. Объединенный тест на несколько коэффициентов регрессии. При помощи F-статистики мы теперь умеем проверять гипотезу о том, что все коэффициенты при объясняющих переменных равны нулю. Иногда возникают ситуации, когда нам необходимо проверить гипотезу о том, что нулю равны не все коэффициенты при объясняющих переменных, а некоторые из них. В этом случае осуществляется следующая процедура. Рассмотрим модель множественной регрессии: Назовем эту модель моделью без ограничений (UR), поскольку здесь мы не делаем никаких ограничений на возможные значения коэффициентов регрессии. Предположим, что мы хотим протестировать гипотезу о том, что q последних коэффициентов регрессии одновременно равны нулю. Т. е. мы хотим проверить гипотезу о том, что нулевая гипотеза выглядит следующим образом: Н0: В случае, если эта гипотеза справедлива, то истинная модель выглядит следующим образом: Назовем эту модель моделью с ограничениями (R –restricted model). Оценим обе эти модели и посчитаем сумму квадратов остатков в модели с ограничениями и в модели без ограничений – ESSR и ESSUR соответственно. ESSR всегда больше, чем ESSUR. Этот результат эквивалентен тому, что R2 всегда увеличивается при добавлении в модель новых объясняющих переменных. Если нулевая гипотеза справедлива, выбрасывание из уравнения q последних объясняющих переменных несильно скажется на объясняющих качествах уравнения, и ESSR будет ненамного отличатся от ESSUR. Таким образом, если нулевая гипотеза справедлива, разница ESSR - ESSUR будет ненамного отличатся от нуля. Статистический критерий для проверки нулевой гипотезы следующий: При справедливости нулевой гипотезы данная статистика имеет распределение Фишера с числом степеней свободы числителя q и знаменателя N-k-1. Если нулевая гипотеза справедлива, выбрасывание из уравнения q последних объясняющих переменных несильно скажется на объясняющих качествах уравнения, и ESSR будет ненамного отличатся от ESSUR. Таким образом, если нулевая гипотеза справедлива, разница ESSR - ESSUR. будет ненамного отличатся от нуля. Следовательно, F-статистика будет достаточно мала. Граничное значение, при котором нулевую гипотезу отвергают, зависит от выбранного уровня значимости . Оно находится из таблиц распределения Фишера для выбранного уровня значимости и числу степеней свободы числителя q и знаменателя N-k-1. Таким образом, если мы нулевую гипотезу отвергаем, то делаем вывод о том, что наши переменные действительно оказывают влияние на переменную Y и включение их в модель существенно повышает объясняющую силу уравнения. Похожий подход – рассмотрение регрессии с ограничение регрессии без ограничений – можно применить и для проверки гипотезы о наличии линейных связей между коэффициентами. Например, нам может понадобиться в ходе нашего исследования проверить гипотезу о равенстве между собой нескольких коэффициентов регрессии.
Предположим, мы рассматриваем и оцениваем функцию потребления: Рассмотрим сначала первый случай. Суть подхода к проверке таких гипотез такая же, как и в предыдущем пункте. Мы оцениваем две регрессии регрессию без ограничений и регрессию с ограничениями, составляем F статистику и проверяем ее значимость при помощи таблиц распределения Фишера. Рассмотрим сначала первый случай. Нулевая гипотеза: H0: Модель без ограничений: модель с ограничениями: Во втором случае моделью с ограничениями будет следующая модель: Здесь мы просто подставили в исходную модель выражение для 2: Статистический критерий для проверки нулевой гипотезы следующий: При справедливости нулевой гипотезы данная статистика имеет распределение Фишера с числом степеней свободы числителя q и знаменателя N-k-1, где q чисто ограничений, накладываемых на коэффициенты. В нашем случае оно равно 1. В статистических пакетах проверка гипотезы о наличии линейных ограничений на коэффициенты называется тестом Вальда (Wald test). Рассмотрим эту гипотезу в общем виде: H0: H = r. Например: 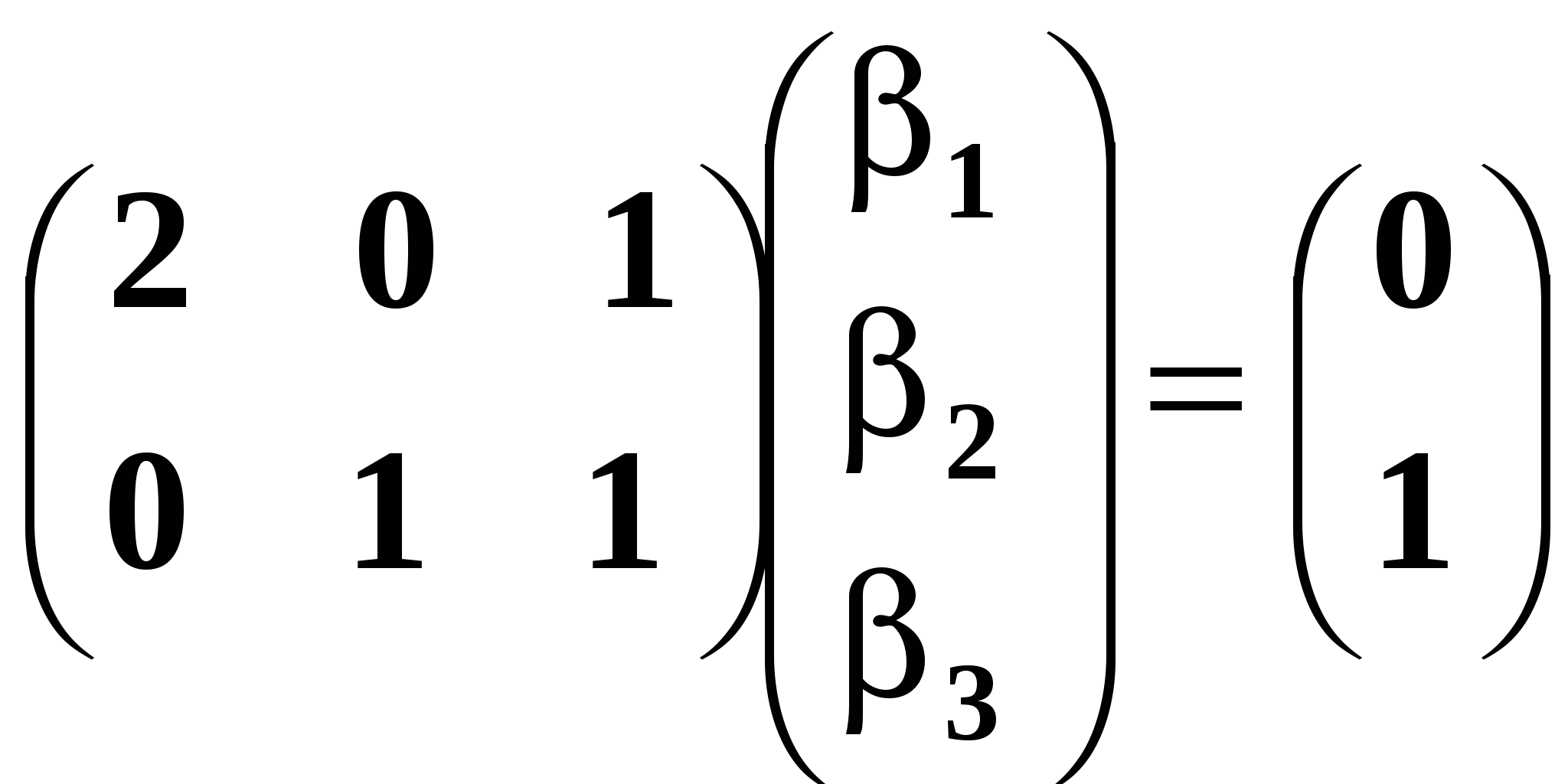 означает, что означает, что H матрица размера Для проверки такой гипотезы используется статистика Вальда: При справедливости нулевой гипотезы эта статистика распределена асимптотически как Ту же самую гипотезу можно проверить при помощи статистики Фишера, вычислив суммы квадратов остатков для моделей с ограничением и модели без ограничений. Как связаны между собой эти статистики? Оказывается, что
|
