лекции по эконометрике. Основные понятия и определения эконометрики
 Скачать 0.78 Mb.
|
9. ГЕТЕРОСКЕДАСТИЧНОСТЬКак было сказано выше, гетероскедастичность – ситуация, когда нарушено пятое условие Гаусса-Маркова: ошибки для разных наблюдений имеют разную дисперсию (  ). Пример с фирмами, работающими в одной сфере. Естественно ожидать, что ошибки для больших фирм будут иметь большую дисперсию, чем ошибки маленьких фирм. Объем продаж, например.
Для случая парной модели  .Интуиция неэффективности. Наблюдение, дисперсия ошибки которого будет меньше, обычно будет находиться ближе к линии регрессии, поэтому будет служить хорошим ориентиром, указывающим место этой линии. Наблюдение же, которое имеет большую дисперсию, будет обычно находится дальше от линии и не сможет существенно помочь в определении местоположения этих линий.
Мы попрежнему рассматриваем модель  Нулевая гипотеза отсутствие в модели гетероскедастичности, т. е. гомоскедастичность: Вид альтернативной гипотезы специфичен для каждого теста, т. е зависит от теста, при помощи которого мы проверяем наличие гетероскедастичности. Не смотря на то, что таких тестов существует несколько, все они базируются на одном: анализе квадратов остатков исходной регрессии. Поскольку остатки регрессии снабжают нас информацией об ошибках регрессии, мы можем проанализировать остатки для того, чтобы посмотреть, отличается ил разброс остатков (вокруг нуля) или разброс наблюдений вдоль линии регрессии от наблюдения к наблюдению разброс остатков вокруг нуля будет отражать разброс ошибок вокруг нуля. Эти рассуждения должны навести нас на мысль, что ситуацию гетероскедастичности можно отследить графически. Если наши данные представляют собой временной ряд, то отсортировав остатки или квадраты остатков по времени и изобразив их на графике мы можем заметить, что остатки растут во времени. Если же мы анализируем пространственные данные, изобразив остатки на графике в зависимости от одной из объясняющих переменных, можно заметить разницу в разбросе остатков. Это эвристический, опытный подход. Теперь приведем несколько формальных тестов. Все тесты предполагают, что дисперсии ошибок наблюдений зависят от некоторой переменной, которая может входить в модель, а может и не входить.
Исходная модель:  Н0:  . Предположим, что нулевая гипотеза неверна и в нашей модели присутствует гетероскедастичность и  . Предположим также, что  , где Zi – может быть одной из объясняющих переменных, группой объясняющих переменных, или вообще переменной, не участвующей в модели. Форма f(Z) может быть различной – линейной, логарифмической, квадратичной.Тест Уайта заключается в следующем:
 В этой регрессии мы учитываем больше форм зависимостей  от независимых переменных. Если нулевая гипотеза справедлива и не зависит никак ни от одной из независимых переменных, то наша регрессия практически ничего не объясняет, следовательно, ее R2 мал. Если же есть гетероскедастичность, то R2 «большой». Границы «малости»: при справедливости нулевой гипотезы статистика  имеет распределение «хи-квадрат» с числом степеней свободы q, где q – число переменных в регрессии пункта 2 вместе со свободным членом.Пример
Задача – уточнить оценки коэффициентов и исправить стандартные ошибки, чтобы модно было пользоваться тестами для проверки гипотез. Предположим ненадолго, что мы знаем величины ошибок  . Тогда поделим обе части уравнения нашей модели на  : , где  .Но  мы никогда не знаем.
Для случая парной модели: ,  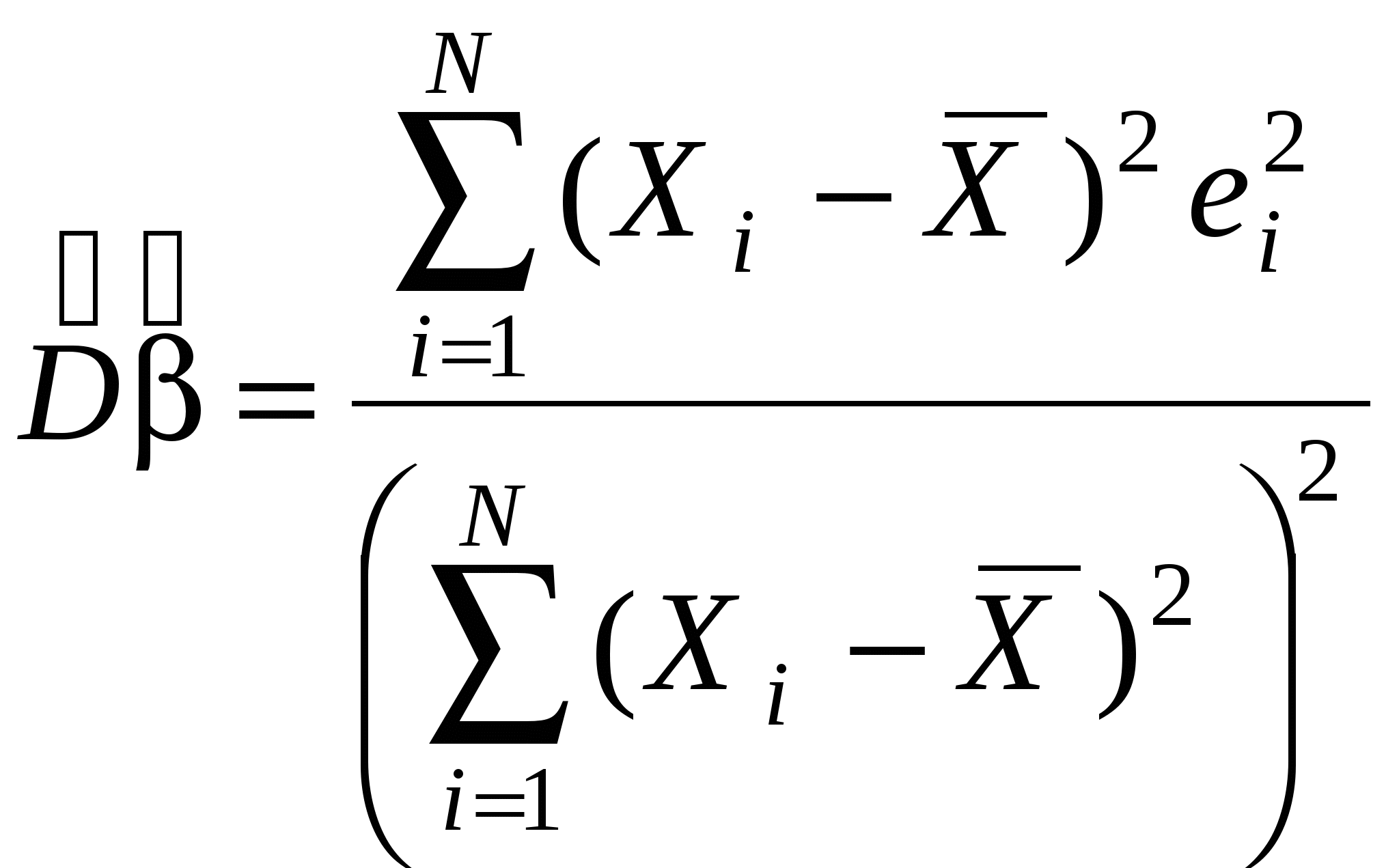.Стандартные ошибки в форме Уайта можно получить практически во всех статистических пакетах, в том числе и в Eviews-е.
Пусть у нас есть основания предполагать, что значения дисперсий ошибок в i-м наблюдении пропорционально значениям некоторой объясняющей переменной (пусть, для определенности, X1), т. е.  или  Тогда мы можем сделать следующее: поделим обе части уравнения нашей модели на  : , где  .Упражнение. Показать, что дисперсия vi не зависит от номера наблюдения. Если же дисперсия ошибок зависит от значений нескольких переменных и форма этой зависимости не обязательно линейная (логарифмическая, например), то проводим двухшаговую процедуру коррекции на гетероскедастичность:
 , получаем 
9. СТОХАСТИЧЕСКИЕ РЕГРЕССОРЫ. До сих пор мы с вами предполагали, что переменные, участвующие в правой части регрессионного уравнения, детерминированные, т. е. не являются случайными. Теперь мы с вами введем в рассмотрение объясняющие переменные, которые берут свои значения из некоторого распределения вероятностей, т. е. являются случайными величинами, со всеми присущиим случайным величинам атрибутами. Как мы увидим, переход от детерминированных регрессоров к случайным при наложении ряда ограничений оставит все наши прежние результаты в силе. Вот эти ограничения:
Все основные свойства МНК-оценок при выполнении условий 7 и 8 сохраняются. | ||||||||
). Дело в том, что 
только в случае выполнения условия Гаусса-Маркова. т. е. дисперсия в условиях гетероскедастичности будет другой, что же на самом деле оценивают 
- ? В этом случае говорят, что МНК-оценки стандартных ошибок смещены. Скорее всего, они занижают истинное значение дисперсии. Теперь мы с вами уже не сможем для оценки гипотезы о значимости коэффициентов пользоваться t-статистиками., поскольку в них фигурируют неверные (смещенные) оценки