лекции по эконометрике. Основные понятия и определения эконометрики
 Скачать 0.78 Mb.
|
|
Эконометрика, часть 1. 1. ЭКОНОМЕТРИЧЕСКОЕ МОДЕЛИРОВАНИЕ. ОСНОВНЫЕ ПОНЯТИЯ И ОПРЕДЕЛЕНИЯ ЭКОНОМЕТРИКИ. Эконометрика – измерения в экономике. Слово «эконометрика» введено в 1926 году норвежским экономистом и статистиком, лауреатом Нобелевской премии Рагнаром Фришем. Современное экономическое образование на западе держится на трех китах: макроэкономике, микроэкономике и эконометрике. В централизованной плановой экономике эконометрика была не нужна, поскольку все планы спускались сверху, не возникало необходимости прогнозировать возможные модели экономического поведения в той или иной ситуации, например. Кроме того, эконометрические методы способны были выявить те или иные нежелательные для властей тенденции экономического развития. В настоящее время наши вузы стали перестраиваться в этом направлении. Почему же эконометрика так важна? Ответить на этот вопрос сложно, и, я надеюсь, что к концу нашего курса вы немного на этот вопрос ответите. Чем больше профессионалом становится экономист, тем он больше понимает, что в экономике все зависит от всего. Для того чтобы понять, каким именно образом выражается эта зависимость, и служат эконометрические методы. Что же за наука эконометрика? Дать определение живой, развивающейся науке, описать ее предмет и метод достаточно трудно. «Эконометрика» – наука об экономических измерениях, но это то же самое, что сказать, что математика – наука о числах. Понятие эконометрика имеет несколько более узкое содержание и назначение, чем это выражено в буквальном переводе и, в то же время, более широкое, чем просто набор статистических инструментов. Современный взгляд на эконометрику отражен в следующем определении: Эконометрика – научная дисциплина, объединяющая совокупность теоретических результатов, приемов, методов и моделей, предназначенных для того, чтобы на базе
придавать конкретное количественное выражение общим (качественным) закономерностям, обусловленным экономической теорией. (С. А. Айвазян, В. С. Мхитарян. Прикладная статистика и основы эконометрики.) Иными словами, эконометрика позволяет на базе положений экономической теории и исходных данных экономической статистики, используя необходимый математико-статистический инструментарий, придавать конкретное количественное выражение общим (качественным) закономерностям. Другие взгляды: Метод экономического анализа, который объединяет экономическую теорию со статистическими и математическими методами анализа. Это попытка улучшить экономические прогнозы и сделать возможным успешное планирование [экономической] политики. В эконометрике экономические теории выражаются в виде математических соотношений, а затем проверяются эмпирически статистическими методами. Данная система используется, чтобы создать модели народного хозяйства с целью прогнозирования таких важных показателей, как валовой национальный продукт, уровень безработицы, темп инфляции и дефицит федерального бюджета. Эконометрика используется все более широко, несмотря на то, что полученные с помощью нее прогнозы не всегда оказывались достаточно точными. The Concise Columbia Electronic Encyclopedia, Third Edition. http://www.encyclopedia.com/ «Подобно математической экономике, эконометрика — это скорее нечто, чем занимаются экономисты, чем определенная предметная область. Эконометрика связана с изучением эмпирических данных статистическими методами; цель этого — проверка гипотез и оценка соотношений, предложенных экономической теорией. В то время как математическая экономика занимается чисто теоретическими аспектами экономического анализа, эконометрика пытается подвергнуть проверке [falsify] теории, которые уже представлены в явной математической форме. Однако часто эти две области экономической науки пересекаются». из статьи Марка Блауга для Британской энциклопедии «Проблемы в эконометрики многочисленны и разнообразны. Экономика — это сложный, динамический, многомерный и эволюционирующий объект, поэтому изучать ее трудно. Как общество, так и общественная система изменяются со временем, законы меняются, происходят технологические инновации, поэтому найти в этой системе инварианты непросто. Временные ряды коротки, сильно агрегированы, разнородны, нестационарны, зависят от времени и друг от друга, поэтому мы имеем мало эмпирической информации для изучения. Экономические величины измеряются неточно, подвержены значительным позднейшим исправлениям, а важные переменные часто не измеряются или ненаблюдаемы, поэтому все наши выводы неточны и ненадежны. Экономические теории со временем меняются, соперничающие объяснения сосуществуют друг с другом, и поэтому надежная теоретическая основа для моделей отсутствует. И среди самих эконометристов, по-видимому, нет согласия по поводу того, как следует заниматься их предметом». из книги Д. Хендри D. F. Hendry, Dynamic Econometrics, Oxford University Press, 1995, p.5. «Существует две вещи, процесс изготовления которых лучше не видеть: сосиски и эконометрические оценки». Э. Лимер E. E. Leamer, "Lets’s Take the Con out of Econometrics," American Economic Review, 73 (1983), 31-43. В редакционной статье, открывающей первый номер журнала Econometrica (старейшего эконометрического журнала) нобелевский лауреат Р. Фриш писал: «... Основной целью [Эконометрического общества] будет стимулирование исследований, которые направлены на объединение теоретико- количественного и эмпирико- количественного подходов к экономическим проблемам, и которые проникнуты конструктивными и строгими рассуждениями того рода, которые преобладают в естественных науках. Но количественный подход к экономике имеет несколько аспектов, и сам по себе ни один из этих аспектов не следует путать с эконометрикой. Таким образом, эконометрика - это ни в коей мере не то же самое, что экономическая статистика. Она также не совпадает и с тем, что мы называем общей экономической теорией, хотя значительная часть этой теории, безусловно, имеет количественный характер. Эконометрику нельзя также рассматривать как синоним применения математики в экономической теории. Опыт показал, что каждая из этих точек зрения, т.е. статистики, экономической теории и математики, является необходимым, но по отдельности не достаточным, условием реального понимания количественных отношений современной экономической жизни. Сила заключается в объединении этих трех элементов. И именно это объединение составляет эконометрику». Frisch, R. "Editorial," Econometrica, 1 (1933), 1-4. Согласно же нашему определению, эконометрика – синтез экономической статистики, экономической теории и математики, наука, связанная с эмпирическим выводом экономических законов, синтез экономической статистики, экономической теории и математики. Т. е. мы используем данные или наблюдения для того, чтобы получить количественные зависимости для экономических законов. Заметим, что отсюда уже следует, что для использования эконометрических методов, нам нужны данные или наблюдения состояния или поведения какого-то экономического объекта. Данные эти как правило, не являются экспериментальными, в отличие от других наук, где используются методы мат. статистики – физики, биологии и др. В экономике мы не можем проводить многократные эксперименты, для того, чтобы проверить правильность наших выводов и в этом специфика экономических данных. Прикладные цели эконометрики.
Как же экономист добивается поставленных перед собой целей. В ходе эконометрического исследования экономист последовательно проходит несколько этапов. Этапы эконометрического моделирования:
На этом этапе процесс формирования значений объясняемой переменной можно представить в виде следующей схемы: X  1,…Xk – выделенные переменные (наиболее существенно влияющие или представляющие для нас определенный интерес).
Таким образом, на этом этапе эконометрист занимается моделированием поведения экономических объектов. Моделирование – упрощение реальности объекта. Задача, искусство моделирования состоит в том, чтобы как можно более лаконично и адекватно именно те стороны реальности, которые интересуют исследователя. Математическая модель схемы:  (1.1).Если  , то уравнение (1) называют уравнение регрессии Y на X1,…Xk . Функция f – регрессионная функция, линия, которую эта функция описывает в пространстве – линия регрессии.Пример с заработной платой и возрастом – заработная плата с возрастом растет. Первая задача – перевести эти предположения на математический язык. К сожалению, проделать это единственным образом нельзя. Что означает возрастающая функция. Есть много функций, которые являются возрастающим функциями своих аргументов. Линейные, нелинейные, разные. Выход – первоначально сформулировать самую простую модель. Введем следующие обозначения для наблюдаемых экономических параметров: W – Заработная плата человека; А – возраст человека; Простейшая модель (линейная):  Уравнение поведения здесь имеют форму точных функциональных зависимостей. Однако, как мы увидим позднее, это нереалистично и нельзя приступать к эконометрической разработке, не пользуясь некоторыми дополнительными стохастическими спецификациями. Мы добавляем в поведенческие уравнения стохастический член. Поскольку ни для каких реальных экономических данных нельзя обеспечить постоянное соблюдение простых соотношений. Кроме того, из всех возможных объясняющих переменных в спецификацию включается лишь небольшое их подмножество, т. е. мы можем говорить только об аппроксимации моделью некоторых, по-видимому достаточно сложных, но неизвестных нам взаимосвязей. Чтобы обеспечить равенство между правой и левой частью, в каждое соотношение приходится вводить случайную ошибку. В нашей модели рассматриваются зависимости между некоторыми переменными. Переменные, значения которых объясняются в рамках нашей модели, называются эндогенными. Переменные, значения которых нашей моделью не объясняются, являются для нее внешними, ничего о том, как формируются эти значения, мы не знаем, называются экзогенными. Еще одна переменная – лаговое значение эндогенной переменной. Она тоже для нашей модели внешняя. Экзогенные переменные и лаговые значения эндогенных переменных – предопределенные переменные. В ходе нашего с вами курса мы с вами столкнемся с несколькими типами эконометрических моделей, которые применяются для анализа и прогноза: а) модели временных рядов. Такие модели объясняют поведение переменной, меняющейся с течением времени, исходя только из его предыдущих значений. К этому классу относятся модели тренда, сезозонности, тренда и сезонности (аддитивная и мультипликативная формы) и др. б) регрессионные модели с одним уравнением. В таких моделях зависимая (объясняемая) переменная представляется в виде функции от независимых (объясняющих) переменных и параметров. В зависимости от вида функции модели бывают линейными и нелинейными. Будем изучать именно их. в) Системы одновременных уравнений. Ситуация экономическая, поведение экономического объекта описывается системой уравнений (наш пример). Системы состоят из уравнений и тождеств, которые могут содержать в себе объясняемые переменные из других уравнений (поэтому вводят понятия экзогенных и эндогенных переменных). Пункт 2 носит название спецификация модели. Необходимо: а) определить цели моделирования; б) определения списка экзогенных и эндогенных переменных; в) определение форм зависимостей между переменными; г) формулировка априорных ограничений на случайный член, что важно для свойств оценок и выбора метода оценивания, и некоторые коэффициенты
Типы данных, с которыми эконометристу приходится сталкиваться при моделировании экономических процессов: а) cross-sectional data – пространственные данные – набор сведений по разным экономическим объектам в один и тот же момент времени; б) time-series data – временные ряды – наблюдение одного экономического параметра в разные периоды или моменты времени. Эти данные естественным образом упорядочены во времени. Инфляция, денежная эмиссия (годовые), курс доллара США (ежедневные); в) panel data – панельные данные – набор сведений по разным экономическим объектам за несколько периодов времени (данные переписи населения).
Итак, эконометрические методы разработаны, в основном, для оценивания параметров экономических моделей. Каждая модель содержит, как правило, несколько уравнений, а в уравнение входит несколько переменных. Начнем с самого простого – парной линейной регрессионной модели. 2. ПАРНЫЙ РЕГРЕССИОННЫЙ АНАЛИЗ. Эконометрические методы разработаны, в основном для оценивания параметров экономических моделей. Каждая модель содержит, как правило, несколько уравнений, а в каждое уравнение входит несколько переменных. Чтобы понять техническую основу, на которой возникают эти достаточно сложные методы, мы начнем с рассмотрения самого простого случая, рассмотрев одно уравнение, которое содержит только две переменных. Итак, у нас есть переменная Y, зависимая или эндогенная, характеризующая результат или эффективность функционирования экономической системы, которую мы анализируем. Ее значения формируются в процессе и внутри функционирования этой системы под воздействием ряда других переменных и факторов. По своему характеру переменная Y всегда случайна. Есть набор объясняющих переменных, экзогенных, характеризующих состояние экономической системы. Эти переменные в существенной степени объясняют процесс формирования эндогенных переменных. Эти переменные, как правило, поддаются хотя бы частичному регулированию и управлению. По своей природе они могут быть как случайными, так и детерминированными. Две переменные могут быть связаны либо функциональной зависимостью (т.е. существует функция f что Y= f(X), значения переменной Y полностью определяются значениями переменной X), либо статистической, либо быть независимыми. Определения.
Приведем пример случайной величины Y, которая не связана с величиной X функционально, а связана корреляционно. Пусть Y – урожай зерна, а X – количество удобрений. С одинаковых по площади участков земли при равных количествах внесенных удобрений снимают различный урожай, т. е. Y не является функцией от X. Это объясняется влиянием случайных факторов (осадки, температура воздуха и др.). Вместе с тем, как показывает опыт, средний урожай является функцией от количества удобрений, т. е. Y связан с X корреляционной зависимостью.
Если каждому значению величины X соответствует свое значение  , то говорят, что существует корреляционная функция = f(X) (2.1)Уравнение (2.1) называют уравнением регрессии Y на X. Т. о. f(X) = M(Y|X=x) – описывает изменение условного среднего значения результирующей переменной в зависимости от изменения значений X объясняющих переменных. Функциональная зависимость наблюдается крайне редко. Тем не мене, большая часть традиционных экономических теорий, в которой связи между экономическими категориями отражаются с помощью формул, имеют дело с точными алгебраическими соотношениями. Однако если мы посмотрим на отдельные наблюдения переменных, фигурирующих в этих законах, то мы увидим, что они не будут точно соответствовать этим соотношениям. (Функция Коба-Дугласа, например). Кроме того, они почти никогда не будут соответствовать любому другому гладкому соотношению. В учебниках по экономической теории эта проблема решается обычно следующим образом: соотношение приводится, как если бы оно было точным, а читателя предупреждают, что это только аппроксимация. Но нас с вами такой подход устраивать не должен. В математической статистике факт точности соотношения признается путем включения в уравнение случайного фактора, описываемого случайным остаточным членом. В простейшей модели Y=+X+. Величина Y, рассматриваемая как зависимая переменная, состоит из двух составляющих:
Откуда берется этот случайный член. Причин может быть несколько и основная:
Если бы мы точно знали, какие переменные сюда входят и как их надо измерять и имели бы возможность точно их измерить, мы бы могли включить их в уравнение, исключив тем самым соответствующий элемент из случайного члена. Проблема состоит в том, что мы никогда не можем быть уверены, что входит в данную совокупность, а что нет. Даже если бы мы включили все эти факторы в уравнение, то мы бы могли оказаться в ситуации, когда число факторов превысило бы число наблюдений так, что любое статистическое усреднение потеряло бы всякий смысл. Итак, мы можем сказать, что вместо зависимости Y= f(X1,…,Xn), где n слишком велико для практических целей, мы рассматриваем зависимость с меньшим числом наиболее важных переменных или переменных, которые представляют для нас наибольший интерес.
Остаточный член является суммарным проявлением всех факторов. Если бы он отсутствовал, мы бы знали, что каждое изменение Y от наблюдения к наблюдению вызвано изменением X и смогли бы точно вычислить коэффициенты. А так каждое изменение Y вызвано изменением X и , поэтому иногда называют шумом. Итак, мы предполагаем, что значения результирующей переменной Y выступают в роли функции, значения которой определяются с некоторой погрешностью значениями объясняющей переменной X, выступающих в роли аргументов этой функции. Математически это может быть выражено в виде уравнения регрессионной связи:  . где  ,  Последнее соотношение в (2.2) следует из смысла функции регрессии, действительно, поскольку  , а M(Y(X)|X)=f(X) по определению, M[f(X)|X]=f(X), поскольку величина f(X) при фиксированных значениях параметра X не является случайной.Содержательные соображения должны подсказать нам форму f(X) – теория, интуиция, опыт, анализ эмпирических данных. Выбор вида функции f(X) – спецификация модели. Одним и тем же условиям могут удовлетворять несколько различных функций, поэтому нам придется обратиться к статистическому анализу и с его помощью осуществить выбор из возможных альтернативных вариантов. Начинают, обычно, с самого простого соотношения между двумя переменными – линейного. (греческие буквы – неизвестные параметры, латинские – оценки) Возможны и другие формы зависимости (примеры). Нас интересуют только те формы зависимости, которые путем преобразования переменных и параметров можно свести к линейным. Т. е. после преобразования переменных и коэффициентов новые переменные и ошибка будут связаны линейным соотношением. Для нелинейных соотношений так же разработан метод оценивания – нелинейный МНК. Рассмотрим парную линейную модель: Y=+X+. Например, мы хотим исследовать зависимость между уровнем заработной платы и возрастом. Для оценки коэффициентов этого уравнения у нас есть набор наблюдений переменной X и соответствующий набор наблюдений переменной Y. Всего у нас N пар чисел (Xi,Yi). Этот набор наблюдений называется выборкой. Расположим их на плоскости. Если бы соотношение между Y и X было бы точным, то соответствующие значения Y лежали бы на прямой. Наличие случайного члена приводит к тому, что в действительности значения Y на прямой не лежат. Рассмотрение ошибок на графике. Yi=+Xi+i – выполняется для каждого наблюдения. , и i нам неизвестны и никогда не будут известны. Мы сможем получить только оценки, хорошие или плохие. Они могут случайным образом совпасть с реальными значениями, но мы этого никогда не узнаем. Каким образом получить эти оценки? Мы предположили, что переменные Y и X связаны линейной зависимостью, т.е. эта зависимость описывается прямой линией. И теперь наша задача – построить прямую. Из всех возможных прямых мы хотим выбрать ту, чтобы она «наилучшим образом» подходила к нашим данным, т. е. отражала бы линейную зависимость Y от X. Иными словами, мы хотим чтобы каждое Yi лежало бы как можно ближе к прямой. В качестве меры близости точек к прямой мы введем разность  - остаток или невязка регрессии. - прогнозное значение переменной Y в i—м наблюдении.Можно сказать, мы хотим, чтобы желаемая прямая была бы в центре скопления наших данных, т. е. чтобы все Yi как можно ближе лежали к нашей прямой. Очевидно, значения a и b надо подбирать таким образом, чтобы минимизировать некоторую интегральную (т. е. по всем имеющимся наблюдениям) характеристику невязок или остатков: МНК – минимизируем 1. Для нахождения минимума функции двух переменных, нам надо взять частные производные по каждой из них и приравнять их к нулю: 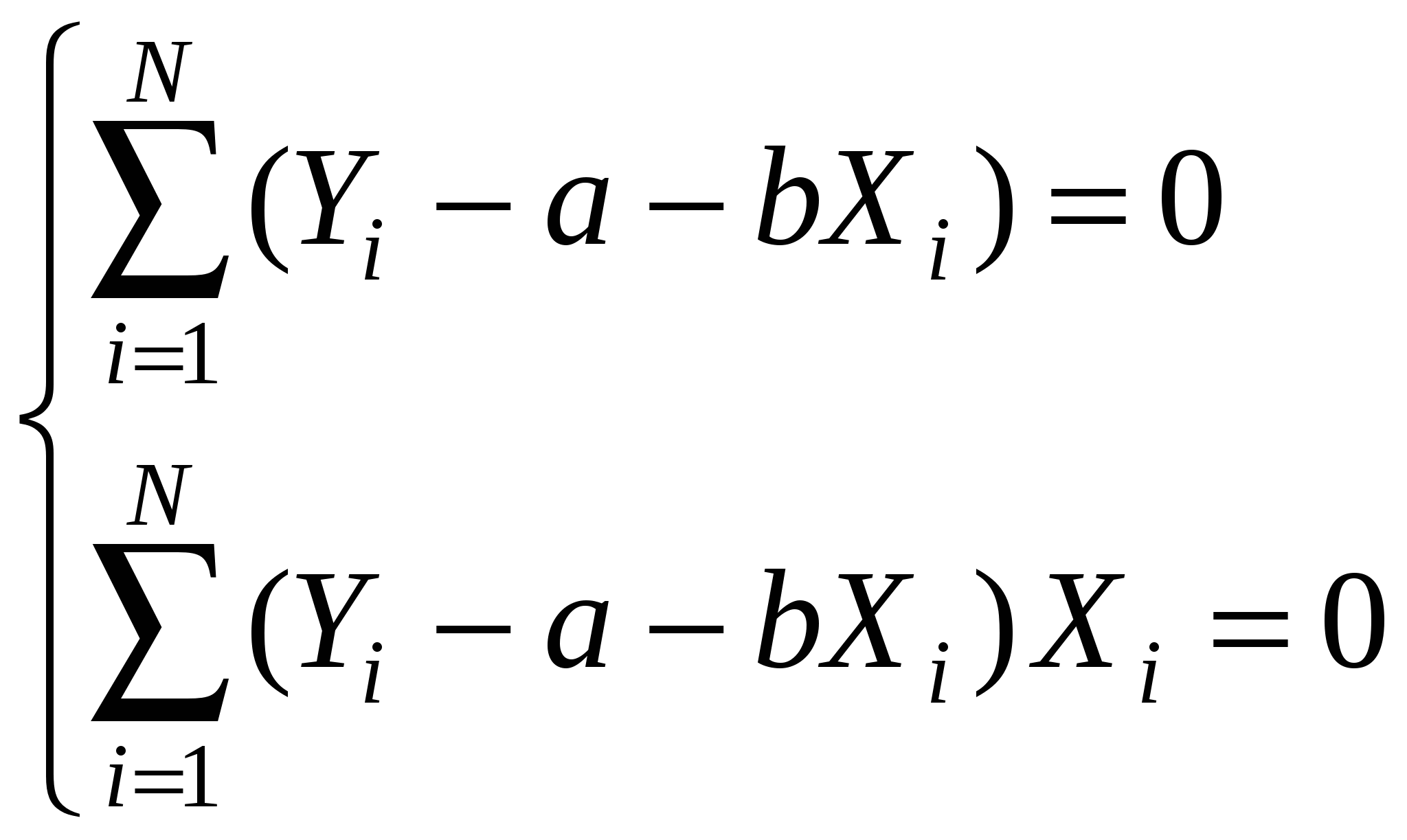  , или  или 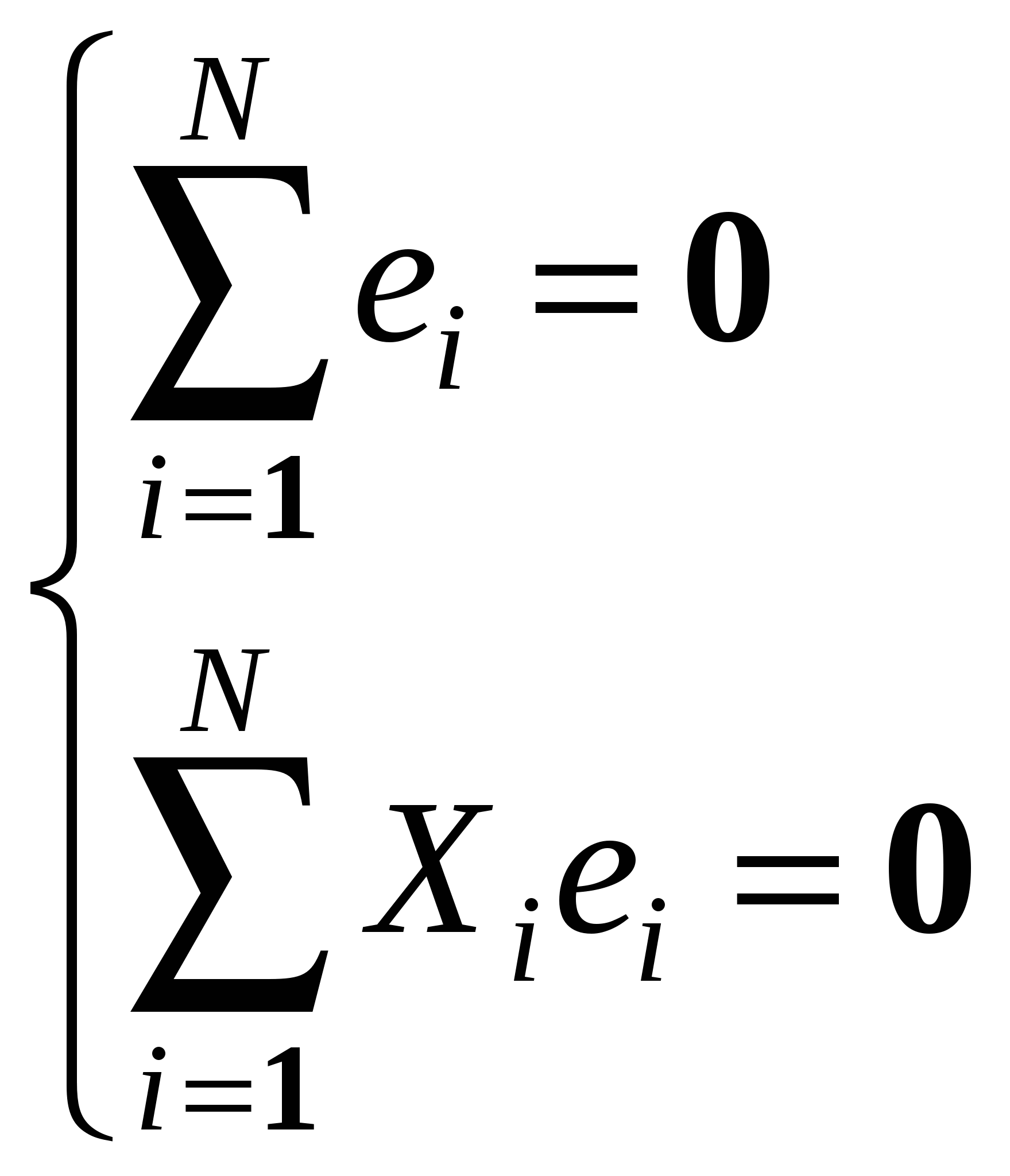 Поделим обе части на N, раскроем скобки и перегруппируем слагаемые, получим  из (2.5) получим, что  .Замечание 1. Линия регрессии проходит через точку  .Замечание 2. Мы предполагаем, что среди Xi есть разные, тогда X 0. 3. МНОЖЕСТВЕННАЯ ЛИНЕЙНАЯ РЕГРЕССИЯ Множественный регрессионный анализ является расширением парного регрессионного анализа на случай, когда зависимая переменная гипотетически связана с более чем одной независимой переменной. В этом случае возникает новая проблема, которой не было в случае парной модели. При оценке влияния данной независимой переменной на зависимую переменную нам надо будет разграничить воздействие на зависимую переменную ее и другие переменные. Кроме того, мы должны будем решить проблему спецификации модели. Если в парном регрессионном анализе эта проблема заключалась только в выборе вида функции f(Х), то теперь нам, кроме этого, надо будет решить, какие мы будем включать в модель, а какие – нет. Иначе говоря, если предполагается, что несколько переменных могут оказывать влияние на зависимую переменную, то другие могут и не подходить для нашей модели. Итак, у нас есть независимая переменная Y, которая характеризует состояние или поведение экономического объекта, и есть набор переменных X1,…,Xk, характеризующие этот экономический объект качественно или количественно, которые, как мы предполагаем, оказывают влияние на переменную Y, т. е. мы предполагаем, что значения результирующей переменной Y выступают в виде функции, значения которой определяются. правда, с некоторой погрешностью, значениями объясняющих переменных, выступающих в роли аргументов этой функции, т. е. Y = f(X1,…,Xk) + , где - случайный член, который входит в наше уравнение по тем же самым причинам, что и в случае парного регрессионного анализа. Поначалу, среди всех возможных функций f(Х1,…,Хk) мы выбираем линейные:  (*) (*) – множественная линейная регрессионная модель (МЛРМ) со свободным членом.  - МЛРМ без свободного члена.Например, если мы изучаем величину спроса на масло, то модель может выглядеть следующим образом:  ,где QD объем спроса на масло, Х доход, P цена на масло, PM цена на мягкое. Здесь нам неизвестны коэффициенты и параметры распределения , Зато мы имеем выборку из N наблюдений над переменными Y и X1,…,Xk. Для каждого наблюдения должно выполнятся следующее равенство:  или в матричной форме: 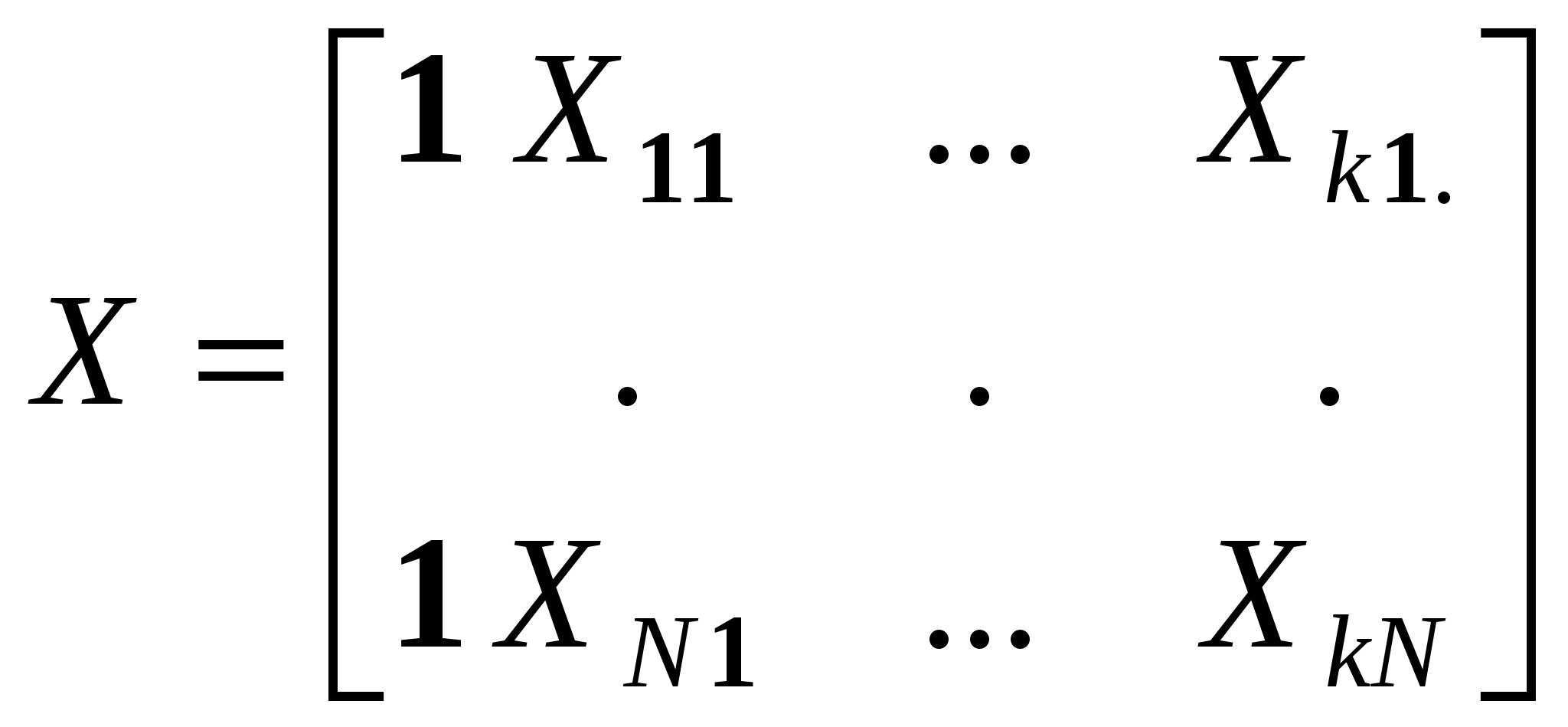 , 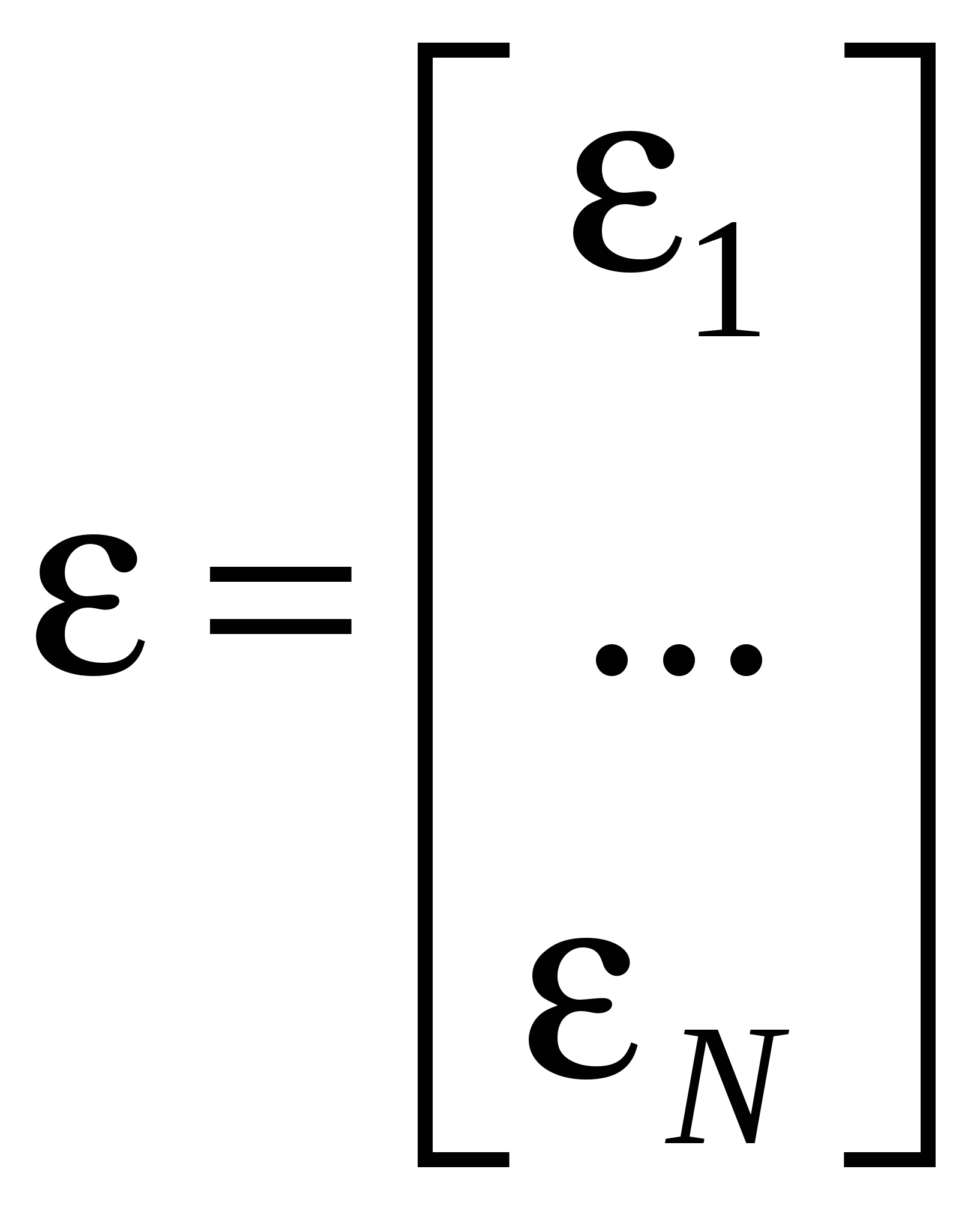где ,  ,  ,  .Наша задача по результатам наблюдений, на основе этих наблюдений, получить надежные оценки неизвестных коэффициентов (оценить неизвестные параметры) и проверить, насколько хорошо выбранная модель соответствует исходным данным. Каким образом получить эти оценки? Нам надо построить гиперплоскость. Из всех возможных гиперплоскостей мы хотим выбрать ту, чтобы она «наилучшим образом» подходила к нашим данным, была бы в центре скопления наших данных, т. е. чтобы все Yi как можно ближе лежали к нашей гиперплоскости. В качестве меры близости точек к прямой мы введем разность   Очевидно, значения b1,…,bk надо подбирать таким образом, чтобы минимизировать некоторую интегральную (т. е. по всем имеющимся наблюдениям) характеристику невязок или остатков:   ,  , тогда  . Здесь мы воспользовались тем, что  - скаляр, и поэтому он совпадает со своим транспонированным значением. Необходимое условие минимума (в матричной форме): .Здесь мы воспользовались свойствами векторного и матричного дифференцирования: Что значит продифференцировать вектор-функцию по вектору переменных: 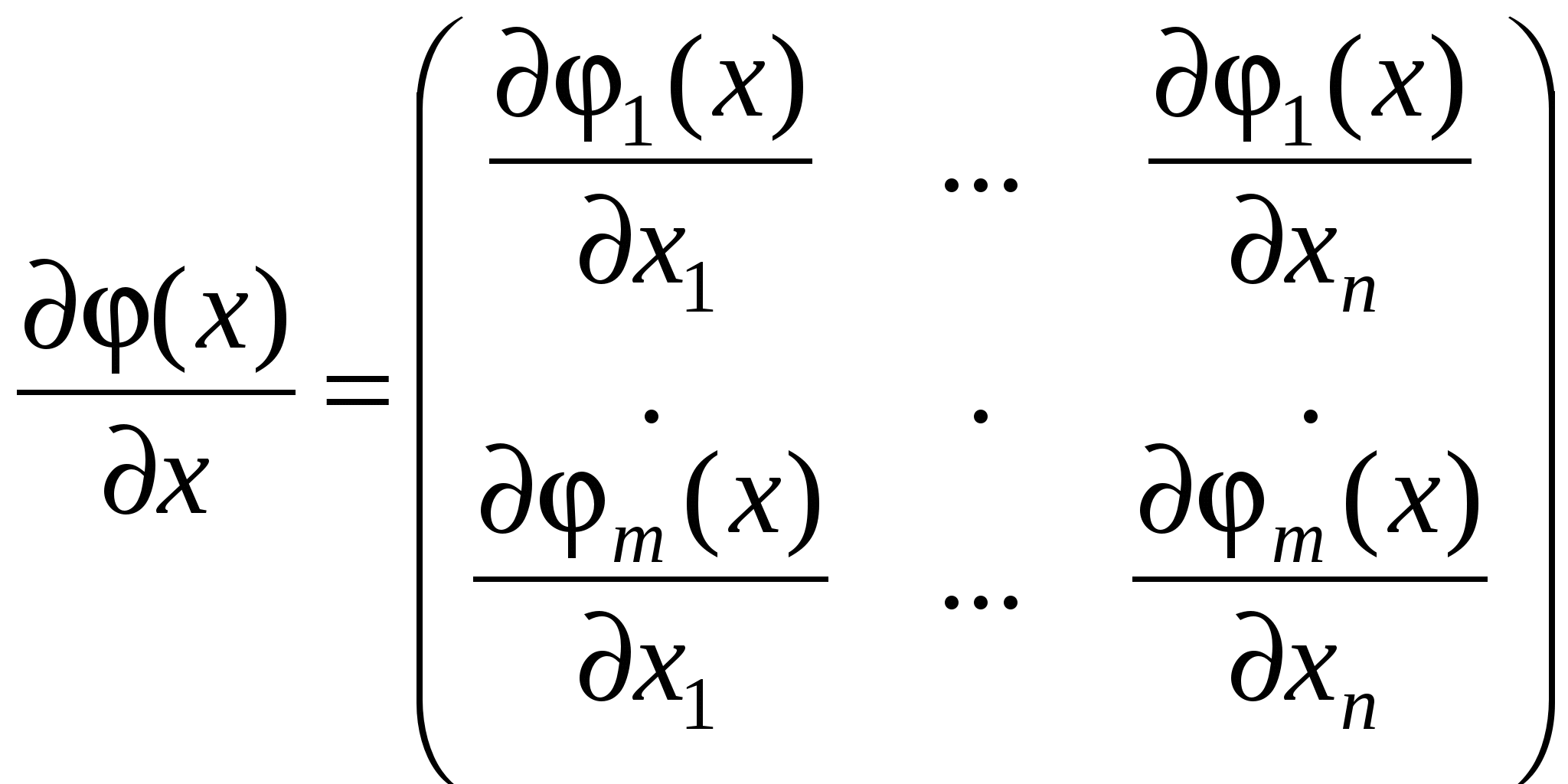 Здесь (х) – m-мерная вектор-функция, х – n-мерный вектор. Случаи:
 , если матрица А симметричная, то
 Итак,    , если матрица  невырождена, то - МНК оценки коэффициентов МЛРМ.Итак, гиперплоскость мы построили. Насколько хорошо нам удалось объяснить изменение переменной Y нашей моделью. Разложим вариацию Y на две части. Насколько наше уравнение объясняет вариацию Y и какова часть Y, которую мы не можем объяснить нашим уравнением. Рассмотрим  - величина, являющаяся мерой вариации переменной Y вокруг ее среднего значения. Распишем эту величину: I II IIIВ этой сумме II = 0, если в уравнении есть свободный член. 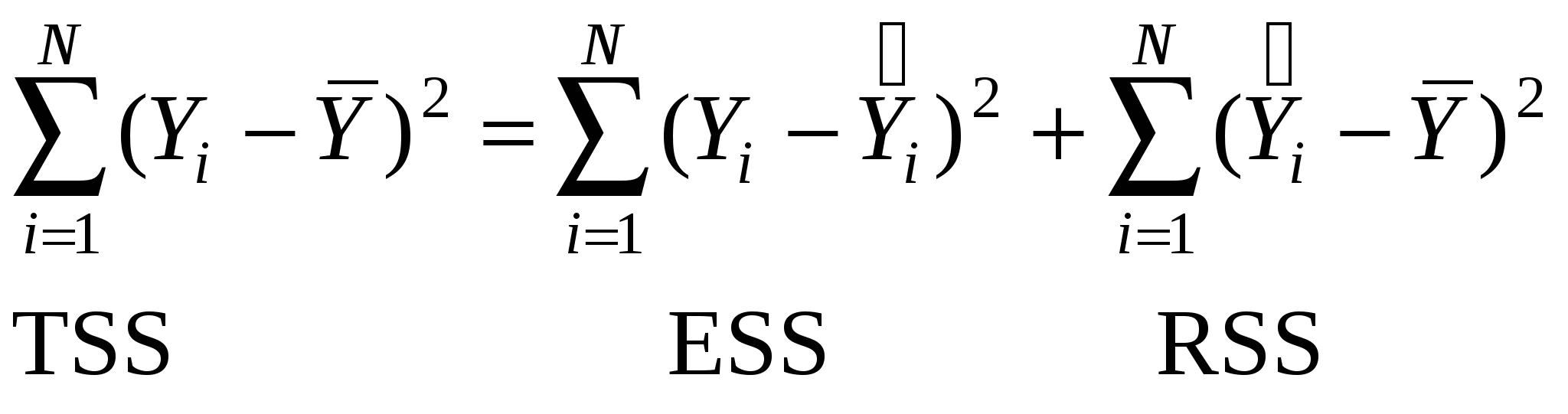 где TSS – total sum of squares – вся дисперсия или вариация Y, характеризует степень случайного разброса значений функции регрессии около среднего значения Y; ESS – error sum of squares – есть сумма квадратов остатков регрессии, та величина, которую мы минимизируем при построении прямой, часть дисперсии, которая нашим уравнением не объясняется; RSS – regression sum of squares – объясненная часть дисперсии. Определение. Коэффициентом детерминации или долей объясненной нашим уравнением дисперсии называется величина  Свойства коэффициента детерминации:
Попыткой устранить эффект, связанный с ростом R2 при увеличении числа регрессоров, является коррекция R2 на число регрессоров - наложение "штрафа" за увеличение числа независимых переменных. Скорректированный R2 - 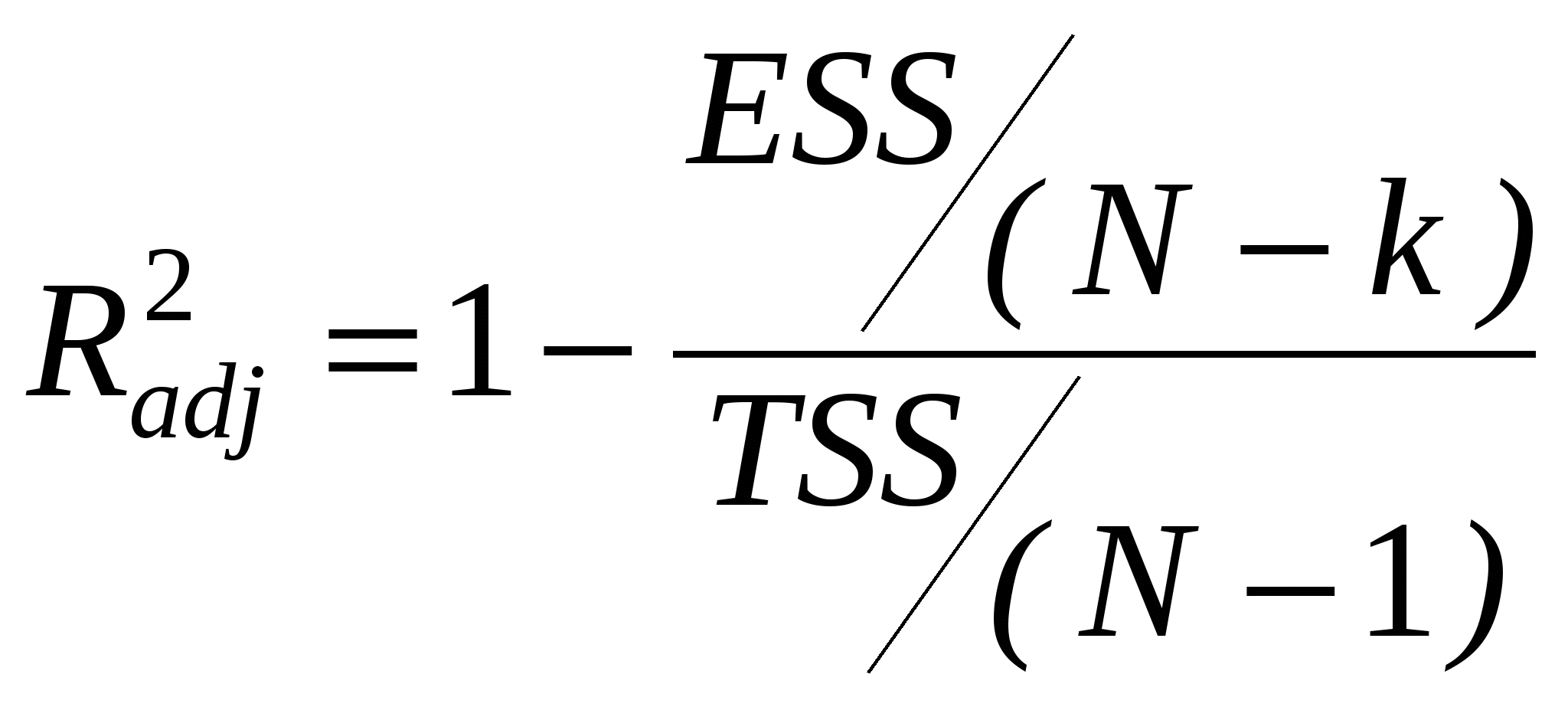 :  (3.9)здесь в числителе - несмещенная оценка дисперсии ошибок (как увидим позднее), в знаменателе - несмещенная оценка дисперсии Y. (Совпадают ли они?). Свойства:
 , k > 1;
В определенном смысле использование для сравнении регрессий при изменении числа регрессоров более корректно.Упражнение. Показать, что статистика увеличится при добавлении новой переменной тогда и только тогда, когда t-статистика коэффициента при этой переменной по модулю больше 1.Следовательно, если в результате регрессии с новой переменной увеличилась, это еще не означает, что коэффициент при этой переменной значимо отличается от нуля, поэтому мы не можем сказать, что спецификация модели улучшилась. Это первая причина, почему не стал широко использоваться в качестве диагностической величины. Вторая причина - уменьшение внимания к самому R2. На практике даже плохо определенная модель регрессии может давать высокий коэффициент R2. Поэтому теперь он рассматривается в качестве одного из целого ряда диагностических показателей, которые должны быть проверены при построении модели регрессии. Следовательно, и корректировка его мало что дает.Итак, при помощи регрессионного анализа мы с вами получили оценки интересующей нас зависимости (*): Однако, это всего лишь оценки. Возникает вопрос, насколько они хороши. Оказывается, что при выполнении некоторых условий наши оценки получаются достаточно надежными. |
, 
, 
, 
- матрица
- матрица.
в силу определения; 
- в это м случае RSS = 0, т. е. наша регрессия ничего не объясняет, ничего не дает по сравнению с тривиальным прогнозом 
. Наши данные позволяют сделать вывод о независимости Yи X, изменение в переменной X никак не влияет на изменение среднего значения переменной Y (примеры, когда зависимость между переменными есть, а коэффициент детерминации равен нулю);
- в этом случае все точки (Xi, Yi) лежат на одной прямой (ESS = 0). Тогда на основании наших данных можно сделать вывод о наличии функциональной, а именно, линейной, зависимости между переменными Y и X. Изменение переменной Y полностью объясняется изменением переменной X; 
- в этом случае чем ближе R2 к 1, тем лучше качество подгонки кривой к нашим данным, тем точнее 
аппроксимирует Y.
- доказать самим;
, k > 1:
, но может быть и < 0.