Ррр. Основные понятия математической логики

• Название: Основные понятия математической логики
• Дата: 03.10.2022
• Размер: 2.23 Mb.
• Имя файла: ege15.doc
• Тип: Закон; #710566
• страница: 20 из 48

Ещё пример задания:

Р-05. На числовой прямой даны два отрезка: P = [2, 20] и Q = [15, 25]. Выберите такой отрезок A, что формула

( (x  А) → (x  P) ) \/ (x  Q)

тождественно истинна, то есть принимает значение 1 при любом значении переменной х.

1) [0, 15] 2) [10, 25] 3) [2, 10] 4)[15, 20]

Решение (отрезки на оси):

1. 
   два условия связаны с помощью операции \/ («ИЛИ»), поэтому должно выполняться хотя бы одно из них
   
2. 
   для того, чтобы упростить понимание выражения, обозначим отдельные высказывания буквами
   

A: x  А, P: x  P, Q: x  Q

3. 
   учтем, что в формуле используется знак  («не принадлежит»), поэтому при переходе к более простым обозначениям получаем:
   

4. 
   представим импликацию через операции «ИЛИ» и «НЕ»: , так что получаем
   
5. 
   это значит, что для тождественной истинности выражения Z нужно, чтобы для любого x было выполнено одно из условий: , , Q; из всех этих выражений нам неизвестно только
   
6. 
   посмотрим, какие интервалы перекрываются условиями 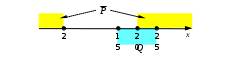иQ; область состоит из двух участков числовой оси, которые не входят в отрезок [2,20], а область Q – это отрезок [15,25]:
   

7. 
   таким образом, область истинности выражения должна перекрывать оставшуюся часть – отрезок [2,15]
   
8. 
   из всех отрезков, приведенных в условии, только отрезок [0,15] (вариант 1) полностью перекрывает отрезок [2,15], это и есть правильный ответ
   
9. 
   Ответ: 1.
   

Решение (таблицы истинности, Е.А. Смирнов):

1. 
   пп. 1-4 такие же, как и в предыдущем способе решения
   
2. 
   если рассматривать все значения x на числовой прямой, то логические значения формул могут измениться только при переходе через граничные точки заданных промежутков
   
3. 
   эти точки (2,15,20 и 25) разбивают числовую прямую на несколько интервалов, для каждого из которых можно определить логическое значение выражения
   

x	P		Q
x < 2	0	1	0	1
2 < x < 15	1	0	0	0
15 < x < 20	1	0	1	1
20 < x < 25	0	1	1	1
x > 25	0	1	0	1

для упрощения записи не будем рассматривать значения формул на концах отрезков, так как это не влияет на решение

4. 
   по условию выражение должно быть равно 1 при любых значениях x, то есть, в соответствующем столбце таблицы должны быть все единицы; отсюда можно найти, каким должно быть значение для каждого интервала:
   

   x	P		Q
   x < 2	0	1	0	1	любое	1
   2 < x < 15	1	0	0	0	1	1
   15 < x < 20	1	0	1	1	любое	1
   20 < x < 25	0	1	1	1	любое	1
   x > 25	0	1	0	1	любое	1

5. 
   таким образом, область истинности выражения должна перекрывать отрезок [2,15]
   
6. 
   из всех отрезков, приведенных в условии, только отрезок [0,15] (вариант 1) полностью перекрывает отрезок [2,15], это и есть правильный ответ
   
7. 
   Ответ: 1.