математика (wecompress.com). Основные теоремы теории вероятностей

• Название: Основные теоремы теории вероятностей
• Дата: 17.05.2023
• Размер: 82.42 Kb.
• Имя файла: математика (wecompress.com).docx
• Тип: Документы; #1138195

Автономная некоммерческая организация высшего образования

«МОСКОВСКИЙ МЕЖДУНАРОДНЫЙ УНИВЕРСИТЕТ»

Кафедра Экономика

Форма обучения: заочная/очно-заочная

ВЫПОЛНЕНИЕ

ПРАКТИЧЕСКИХ ЗАДАНИЙ

ПО ДИСЦИПЛИНЕ

МАТЕМАТИКА

Группа Ал21Э211в

Студент: Шаниязов Муратбай Оразбай улы

МОСКВА 2022

Основные теоремы теории вероятностей

Классическое определение вероятности

Вероятностью события А называется отношение чсла исходов m, благоприятствующих его наступлению к числу всех исходов n (несовместных, единственно возможных и равновозможных): 

 P(A) = m/n.

Будем различать достоверные и невозможные события. По определению, их вероятности соответственно равны 1 и 0.

Геометрическое определение вероятности

Если число исходов некоторого опыта бесконечно, то
классическое определение вероятности не может служить характеристикой степени возможности наступления того или иного события. В этом случае пользуются геометрическим подходом к определению вероятности. При этом вероятность события A есть отношение меры A (длины, площади, объема) к мере U пространства элементарных событий.

Теоремы о вероятностях событий

Произведением событий A и B называется событие C = A• B, состоящее в том, что в результате испытания произошло и событие A, и событие B, т. е. оба события произошли.

Два событияA иB называются независимыми, если вероятность появления каждого из них не зависит от того, появилось другое событие или нет. В противном случае события A и B называются зависимыми.

Теорема. Вероятность произведения двух независимых событий A и B равна произведению этих вероятностей: P(AB) = P(A) • P(B).

Противоположные события

Два события называются совместными, если появление одного из них не исключает появление другого в одном и том же испытании.

Два события называются противоположными, если в данном испытании они несовместны и одно из них обязательно происходит. Вероятности противоположных событий в сумме дают 1.

Если событие A может произойти с вероятностью p и опыт повторяют n раз, то вероятность, что оно наступит хотя бы один раз, есть: 1 - qⁿ, где q = 1 - p.

Сложение вероятностей

Суммой событий A и B называется событие C = A + B, состоящее в наступлении, по крайней мере, одного из событий A или B, т. е. в наступлении события A, или события B, или обоих этих событий вместе, если они совместны.

Теорема. Вероятность суммы двух несовместных событий A и B равна сумме вероятностей этих событий: P(A+B) = P(A) + P(B).

Условная вероятность

Пусть A и B— зависимые события. Условной вероятностью P_A(B) события B называется вероятность события B, найденная в предположении, что событие A уже наступило.

Теорема. Вероятность произведения двух зависимых событий A и B равна произведению вероятности одного из них на условную вероятность другого, найденного в предположении, что первое событие уже наступило: P(AB) = P(A) • P_A(B).

Теорема. Вероятность суммы двух совместных событий A и B равна сумме вероятностей этих событий минус вероятность их произведения: P (A + B) = P(A) + P(B) – P(AB).

Формула Бернулли

Для многократно повторяемых опытов справедлива формула Бернулли:

P _m, n = C _n^m • p^m •q ^n-m, где m — число удачных исходов среди проводимых n опытов, p — вероятность наступления благоприятного исхода в единичном опыте, q = 1 – p.

Рассмотрим некоторые задачи с решениями. 

Задание 5. № 319353. Две фабрики выпускают одинаковые стекла для автомобильных фар. Первая фабрика выпускает 45% этих стекол, вторая — 55%. Первая фабрика выпускает 3% бракованных стекол, а вторая — 1%. Найдите вероятность того, что случайно купленное в магазине стекло окажется бракованным.

Решение.
Вероятность того, что стекло куплено на первой фабрике и оно бракованное: 0,45 · 0,03 = 0,0135.

Вероятность того, что стекло куплено на второй фабрике и оно бракованное: 0,55 · 0,01 = 0,0055.

Поэтому по формуле полной вероятности вероятность того, что случайно купленное в магазине стекло окажется бракованным равна 0,0135 + 0,0055 = 0,019. 

Ответ: 0,019.

Задание 5. № 319355. Если гроссмейстер А. играет белыми, то он выигрывает у гроссмейстера Б. с вероятностью 0,52. Если А. играет черными, то А. выигрывает у Б. с вероятностью 0,3. Гроссмейстеры А. и Б. играют две партии, причем во второй партии меняют цвет фигур. Найдите вероятность того, что А. выиграет оба раза.

Решение.
Возможность выиграть первую и вторую партию не зависят друг от друга. Вероятность произведения независимых событий равна произведению их вероятностей: 0,52 · 0,3 = 0,156.

Ответ: 0,156

Задание 5. № 320171. На экзамене по геометрии школьнику достаётся один вопрос из списка экзаменационных вопросов. Вероятность того, что это вопрос на тему «Вписанная окружность», равна 0,2. Вероятность того, что это вопрос на тему «Параллелограмм», равна 0,15. Вопросов, которые одновременно относятся к этим двум темам, нет. Найдите вероятность того, что на экзамене школьнику достанется вопрос по одной из этих двух тем.

Решение.
Вероятность суммы двух несовместных событий равна сумме вероятностей этих событий: 0,2 + 0,15 = 0,35.

Ответ: 0,35.

5. № 320172. В торговом центре два одинаковых автомата продают кофе. Вероятность того, что к концу дня в автомате закончится кофе, равна 0,3. Вероятность того, что кофе закончится в обоих автоматах, равна 0,12. Найдите вероятность того, что к концу дня кофе останется в обоих автоматах.

Решение.
Рассмотрим события 


А = кофе закончится в первом автомате,
В = кофе закончится во втором автомате. 

Тогда


A·B = кофе закончится в обоих автоматах,
A + B = кофе закончится хотя бы в одном автомате. 


По условию P(A) = P(B) = 0,3; P(A·B) = 0,12.

События A и B совместные, вероятность суммы двух совместных событий равна сумме вероятностей этих событий, уменьшенной на вероятность их произведения: 


P(A + B) = P(A) + P(B) − P(A·B) = 0,3 + 0,3 − 0,12 = 0,48. 


Следовательно, вероятность противоположного события, состоящего в том, что кофе останется в обоих автоматах, равна 1 − 0,48 = 0,52.

Ответ: 0,52.

Можно привести и другое решение.
Вероятность того, что кофе останется в первом автомате равна 1 − 0,3 = 0,7. Вероятность того, что кофе останется во втором автомате равна 1 − 0,3 = 0,7. Вероятность того, что кофе останется в первом или втором автомате равна 1 − 0,12 = 0,88. Поскольку P(A + B) = P(A) + P(B) − P(A·B), имеем: 0,88 = 0,7 + 0,7 − х, откуда искомая вероятность х = 0,52.

Примечание.
Важно понимать, что события А и В не являются независимыми. Действительно, вероятность произведения независимых событий была бы равна произведению вероятностей этих событий: P(A·B) = 0,3·0,3 = 0,09, однако по условию эта вероятность равна 0,12.

Задание 5. № 320173. Биатлонист пять раз стреляет по мишеням. Вероятность попадания в мишень при одном выстреле равна 0,8. Найдите вероятность того, что биатлонист первые три раза попал в мишени, а последние два промахнулся. Результат округлите до сотых.

Решение.
Поскольку биатлонист попадает в мишени с вероятностью 0,8, он промахивается с вероятностью 1 − 0,8 = 0,2. События попасть или промахнуться при каждом выстреле независимы, вероятность произведения независимых событий равна произведению их вероятностей. Тем самым, вероятность события «попал, попал, попал, промахнулся, промахнулся» равна 

                                              0,8 ∙ 0,8 ∙ 0,8 ∙ 0,2 ∙ 0,2 = 0,02048 ≈ 0,02

Ответ: 0,02.

Задание 5. № 320174. В магазине стоят два платёжных автомата. Каждый из них может быть неисправен с вероятностью 0,05 независимо от другого автомата. Найдите вероятность того, что хотя бы один автомат исправен. 

Решение.
Найдем вероятность того, что неисправны оба автомата. Эти события независимые, вероятность их произведения равна произведению вероятностей этих событий: 0,05 · 0,05 = 0,0025.

Событие, состоящее в том, что исправен хотя бы один автомат, противоположное. Следовательно, его вероятность равна 1 − 0,0025 = 0,9975.

Ответ: 0,9975.


Есть другое решение.
Вероятность того, что исправен первый автомат (событие А) равна 0,95. Вероятность того, что исправен второй автомат (событие В) равна 0,95. Это совместные независимые события. Вероятность их произведения равна произведению вероятностей этих событий, а вероятность их суммы равна сумме вероятностей этих событий, уменьшенной на вероятность их произведения. Имеем: 


P(A + B) = P(A) + P(B) − P(A·B) = P(A) + P(B) − P(A)P(B) = 0,95 + 0,95 − 0,95·0,95 = 0,9975.

Основные теоремы теории вероятностей

Дата публикации   16.03.2012 |



На практике обычно требуется определить вероятность событий, непосредственное экспериментальное воспроизведение которых затруднено.

Обычно такая оценка и производится с целью выявления наиболее рациональных конструктивных параметров элементов перспективной техники.

Поэтому, как правило, для определения вероятностей событий применяются не непосредственные прямые методы, а косвенные, позволяющие по известным вероятностям одних событий определять вероятности других событий, с ними связанных.

Применяя эти косвенные методы, мы всегда в той или иной форме пользуемся основными теоремами теории вероятностей. Этих теорем две:
• теорема сложения вероятностей;
• теорема умножения вероятностей.

Введем понятие о сумме событий и произведении событий.
Суммой двух событий А и В называется событие С состоящее в появлении хотя бы одного из событий А и В. Суммой нескольких событий называется событие, состоящее в появлении хотя бы одного из этих событий.

Геометрическая интерпретация: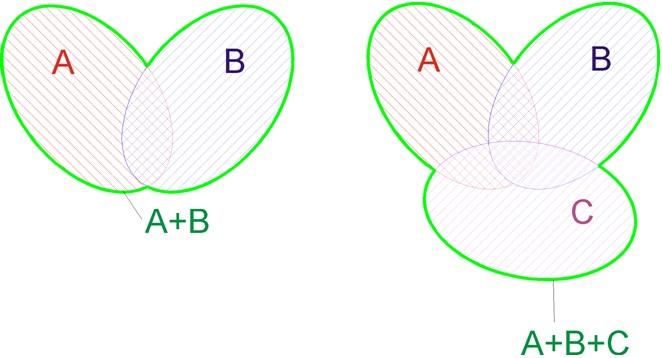




Произведением двух событий А и В называется событие С, состоящее в совместном выполнении события А и В. Произведением нескольких событий называется событие, состоящее в совместном появлении всех этих событий.

Геометрическая интерпретация: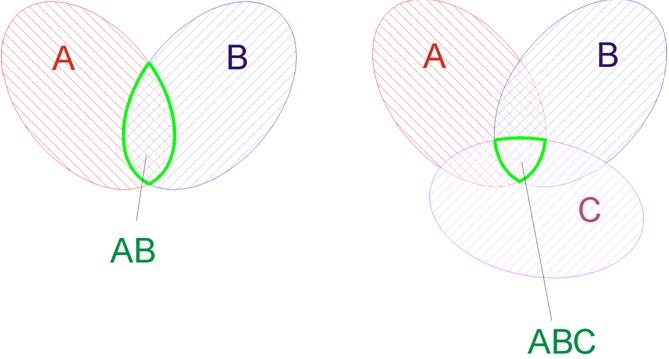



Теорема сложения вероятностей

Вероятность суммы двух несовместных событий равна сумме вероятностей этих событий:

Р(А+В) = Р(А) + Р(В) (1)

Теорема сложения вероятностей применима к любому числу несовместных событий. В общем виде ее удобно записать:

Р(∑A_i) = ∑Р(A_i) (2)

Отметим следствия вытекающие из теоремы сложения вероятностей.

Следствие 1: Если события А₁, А₂, …, А_n образуют полную группу несовместных событий, то сумма их вероятностей равна единице:

∑Р(A_i) = 1 (3)

Перед тем как вывести второе следствие теоремы сложения, введем понятие «противоположные события».

Противоположными событиями называются два несовместных события, образующих полную группу. Событие противоположное событию А принято обозначать A.

Пример:
Событие А – безотказная работа всех элементов технической системы; A — отказ хотя бы одного элемента.

Следствие 2: Сумма вероятностей противоположных событий равна единице:

P(A) + P(A) =1 (4)

Следствие 2 есть частный случай следствия 1.

Вероятность суммы двух совместных событий выражается формулой:

Р(А+В) = Р(А) + Р(В) – P(AB) (5)

Аналогично вероятность суммы трех совместных событий вычисляется по формуле:

Р(А+В+С) = Р(А) + Р(В) + Р(С) – P(AB) – P(AС) – P(ВС) + Р(АВС) (6)

Общая формула для вероятности суммы любого числа совместных событий:

Р(∑A_i) = ∑Р(A_i) — ∑Р(A_iA_j) + ∑Р(A_iA_jA_k) — (-1)^n-1P(A₁A₂…A_n) (7)

где суммы распространяются на различные значения индексов i; i, j; i, j, k и т.д.

Из формул (5) и (6) можно записать аналогичную формулу для произведения событий

P(AB) = Р(А) + Р(В) – Р(А+В) (8)

Р(АВС) = Р(А) + Р(В) + Р(С) – P(A+B) – P(A+С) – P(В+С) + Р(А+В+С) (9)

Теорема умножения вероятностей

Введем понятие независимые и зависимые события.

Событие А называется независимым от события В, если вероятность события А не зависит от того, произошло событие В или нет.

Событие А называют зависимым от события В, если вероятность события А меняется в зависимости от того, произошло событие В или нет.

Вероятность события А, вычисленная при условии, что имело место другое событие В, называется условной вероятностью события А и обозначается Р (А/В)

Пример:
В урне два белых и один черный. Два лица вынимают из урны по одному шару. Рассматриваются события: А- появление белого шара у 1-го лица; В – появление белого шара у 2-го лица.
Решение: Р(А) до того как произошло событие В равно 2/3. Если событие В произошло, то Р(А)=1/2. Таким образом, событие А зависит от события В.

Условие независимости события А от события В можно записать в виде:

Р(А/В) = P(A) (10)

а, условие зависимости: Р(А/В) ≠ P(A) (11)

Теорема умножения: Вероятность произведения двух событий равна произведению вероятности

Р(АВ) = P(A)⋅Р(В/А) (12)

Вероятность произведения нескольких событий равна произведению вероятностей этих событий, причем вероятность каждого следующего по порядку события вычисляется при условии, что все предыдущие имели место:

Р(А₁А₂…А_n ) = P(A₁)⋅Р(А₂/А₁)⋅Р(А₃/А₁А₂)⋅…⋅Р(А_n/А1А2…А n-1) (13)

Следствие 1: Если событие А не зависит от события В, то и событие В не зависит от события А

Следствие 2: Вероятность произведения двух независимых событий равна произведению вероятностей этих событий

P(AВ) = P(А)⋅Р(В) (14)
Р(А₁А₂…А_n ) = P(A₁)⋅Р(А₂)⋅….⋅Р(А_n) (15)

Формула полной вероятности

Следствием основных теорем является так называемая формула полной вероятности.

Пусть требуется определить вероятность некоторого события А, которое может произойти вместе с одним из событий:
Н₁, Н₂, ….Н_n,
Образующих полную группу несовместных событий. Будем эти события называть гипотезами.

В этом случае, вероятность события А вычисляется как сумма произведений вероятности каждой гипотезы на вероятность события при этой гипотезе

Р(А)=∑Р(H_i)⋅P(A/H_i) (16)

Теорема гипотез (формула Бейеса)

Имеется полная группа несовместных гипотез Н₁, Н₂, …., Н_n. Вероятности этих гипотез до опыта известны и равны соответственно Р(Н₁), Р(Н₂)…. Р(Н_n).

Произведен опыт, в результате которого наблюдалось появление некоторого события А. Как следует изменить вероятность гипотез в связи с появлением этого события? По существу речь идет о том, чтобы найти условную вероятность Р(Н_i/А) для каждой гипотезы.

Р(Н_i/А) = [Р(Н_i)⋅Р(Н_i/A] / [∑Р(H_i)⋅P(A/H_i)], i = 1, 2, …, n (17)