+для статьи_ММлесн.экосистем. Основные типы моделей

• Название: Основные типы моделей
• Дата: 07.07.2018
• Размер: 146.52 Kb.
• Имя файла: +для статьи_ММлесн.экосистем.docx
• Тип: Документы; #48398
• страница: 1 из 12

Основные типы моделей

Математическое моделирование - один из основных инструментов системного анализа, позволяющий в ряде случаев избежать трудоемких и дорогостоящих натурных экспериментов. На основе результатов прогнозирования динамики геосистем решаются вопросы рационального применения удобрений и средств защиты растений, проведения комплексной мелиорации и окультуривания полей, оптимизации структуры землепользования и другие. Ведутся исследования в области организации "ландшафтного земледелия" - оптимизации сельскохозяйственного использования земель в зависимости от местных условий (рельефа, климата, почвенных условий, размещения других хозяйственных объектов)

Диапазон и масштаб моделируемых процессов крайне велик - от глобальной экологии до прогнозирования динамики отдельных компонентов агроценозов, поэтому при классификации экологических моделей могут быть использованы различные подходы. Многие авторы выделяют статические и динамические модели Статические модели формализуют связь между показателями без учета переменной времени. Динамические модели используются для оценки явлений в развитии. Функциональные модели отличаются от эмпирических тем, что учитывают механизм процесса. Это позволяет использовать их для прогноза не наблюдавшихся ранее состояний объекта. Различие между стохастическими и детерминированными моделями следует из их названия. При описании неопределенных процессов в природных системах (агрометеорологические условия, миграция веществ по профилю почв, трансформация пестицидов, выделение границ почвенных ареалов, возникновение вспышек болезней растений, динамика численности вредителей и иных) более предпочтительно использовать вероятностные подходы. Важнейшей задачей моделирования является прогнозирование и управление объектом, выделяются модели без управления и оптимизационные (с участием одной или нескольких сторон).

Наиболее часто применяются: статистические, модели математической физики (диффузные), балансовые динамические, матричные модели, модели теории исследования операций, частные модели типа "ресурс-потребитель" и аналогичные им, а также целая группа дискретных математических моделей

Статистические модели экологии и почвовед

Статистические модели – это обычно алгоритмы со случайным характером значений используемых переменных и связей между операторами.

[+] высокая точность, возможность учета очень многих параметров, также нет допущений.

[-] громоздкая, для ее исследования требуются большие затраты времени, плохая обозримость модели до специальной (вторичной) обработки, сложно выявить присущие модели закономерности (не можем менять по одному параметру…), сложно получить оптимальный результат.

Пример: разработка телефонной станции. Используется метод статистического моделирования, случайным образом формируются данные для работы какого-либо объекта.

По степени отражения времени модели делятся на статические, динамические и кинематические.

Статические модели – модели состояния объекта в определенный, фиксированный момент времени. Для описания статической модели используются алгебраические или булевские уравнения (пример – модель комбинационной схемы – проверяем закон функционирования, однократное обращение к модели – одна строка таблицы истинности). Статическая модель – в некотором приближении проверка закона функционирования.

Нормальное распределение, также называемое распределением Гаусса — распределение вероятностей, которое в одномерном случае задается функцией плотности вероятности, совпадающей с функцией Гаусса: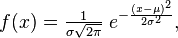



где параметр μ — математическое ожидание, медиана и мода распределения, а параметр σ — стандартное отклонение (σ² — дисперсия) распределения.

Таким образом, одномерное нормальное распределение является двухпараметрическим семейством распределений. Многомерный случай описан в многомерном нормальном распределении.

Стандартным нормальным распределением называется нормальное распределение с математическим ожиданием μ = 0 и стандартным отклонением σ = 1. Генеральная совокупность – это совокупность всех мысленно возможных объектов данного вида, над которыми проводятся наблюдения с целью получения конкретных значений определенной случайной величины.

Генеральная совокупность может быть конечной или бесконечной в зависимости от того, конечна или бесконечна совокупность составляющих ее объектов.

Выборкой (выборочной совокупностью)называется совокупность случайно отобранных объектов из генеральной совокупности.

Выборка должна быть репрезентативной (представительной), то есть ее объекты должны достаточно хорошо отражать свойства генеральной совокупности.

Выборка может быть повторной, при которой отобранный объект (перед отбором следующего) возвращается в генеральную совокупность, и бесповторной, при которой отобранный объект не возвращается в генеральную совокупность

Применяют различные способы получения выборки.

1) Простой отбор – случайное извлечение объектов из генеральной совокупности с возвратом или без возврата.

2) Типический отбор, когда объекты отбираются не из всей генеральной совокупности, а из ее «типической» части.

3) Серийный отбор – объекты отбираются из генеральной совокупности не по одному, а сериями.

4) Механический отбор - генеральная совокупность «механически» делится на столько частей, сколько объектов должно войти в выборку и из каждой части выбирается один объект.

Число объектов генеральной совокупности и число объектов выборки называют объемами генеральной и выборочной совокупностей соответственно. При этом предполагают, что (значительно больше).