+для статьи_ММлесн.экосистем. Основные типы моделей

• Название: Основные типы моделей
• Дата: 07.07.2018
• Размер: 146.52 Kb.
• Имя файла: +для статьи_ММлесн.экосистем.docx
• Тип: Документы; #48398
• страница: 4 из 12

Метод наименьших квадратов

Метод наименьших квадратов — математический (математико-статистический) прием, служащий для выравнивания динамических рядов, выявления формы корреляционной связи между случайными величинами и др. Состоит в том, что функция, описывающая данное явление, аппроксимируется более простой функцией. Причем последняя подбирается с таким расчетом, чтобы среднеквадратичное отклонение (см.Дисперсия) фактических уровней функции в наблюдаемых точках от выровненных было наименьшим.

Напр., по имеющимся данным (x_i,y_i) (i = 1, 2, ..., n) строится такая кривая y = a + bx, на которой достигается минимум суммы квадратов отклонений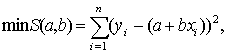



т. е. минимизируется функция, зависящая от двух параметров: a — отрезок на оси ординат и b — наклон прямой.

Уравнения, дающие необходимые условия минимизации функции S(a,b), называются нормальными уравнениями. В качестве аппроксимирующих функций применяются не только линейная (выравнивание по прямой линии), но и квадратическая, параболическая, экспоненциальная и др. Пример выравнивания динамического ряда по прямой см. на рис. M.2, где сумма квадратов расстояний (y₁ – ȳ₁)² + (y₂ – ȳ₂)² .... — наименьшая, и получившаяся прямая наилучшим образом отражает тенденцию динамического ряда наблюдений за некоторым показателем во времени.

Для несмещенности МНК-оценок необходимо и достаточно выполнения важнейшего условия регрессионного анализа: условное по факторам математическое ожидание случайной ошибки должно быть равно нулю. Данное условие, в частности, выполнено, если: 1.математическое ожидание случайных ошибок равно нулю, и 2.факторы и случайные ошибки — независимые случайные величины. Первое условие можно считать выполненным всегда для моделей с константой, так как константа берёт на себя ненулевое математическое ожидание ошибок. Второе условие — условие экзогенности факторов — принципиальное. Если это свойство не выполнено, то можно считать, что практически любые оценки будут крайне неудовлетворительными: они не будут даже состоятельными (то есть даже очень большой объём данных не позволяет получить качественные оценки в этом случае).

Наиболее распространенным в практике статистического оценивания параметров уравнений регрессии является метод наименьших квадратов. Этот метод основан на ряде предпосылок относительно природы данных и результатов построения модели. Основные из них - это четкое разделение исходных переменных на зависимые и независимые, некоррелированность факторов, входящих в уравнения, линейность связи, отсутствие автокорреляции остатков, равенство их математических ожиданий нулю и постоянная дисперсия.

Одной из основных гипотез МНК является предположение о равенстве дисперсий отклонений еi, т.е. их разброс вокруг среднего (нулевого) значения ряда должен быть величиной стабильной. Это свойство называется гомоскедастичностью. На практике дисперсии отклонений достаточно часто неодинаковы, то есть наблюдается гетероскедастичность. Это может быть следствием разных причин. Например, возможны ошибки в исходных данных. Случайные неточности в исходной информации, такие как ошибки в порядке чисел, могут оказать ощутимое влияние на результаты. Часто больший разброс отклонений єi, наблюдается при больших значениях зависимой переменной (переменных). Если в данных содержится значительная ошибка, то, естественно, большим будет и отклонение модельного значения, рассчитанного по ошибочным данным. Для того, чтобы избавиться от этой ошибки нам нужно уменьшить вклад этих данных в результаты расчетов, задать для них меньший вес, чем для всех остальных. Эта идея реализована во взвешенном МНК.

Пространственные модели в экологии и почвоведении

Для решения информационных и расчетных задач, анализа, моделирования, отображения обстановки и местности многочисленные пользователи применяют пространственные (трехмерные) модели местности. Вместе с электронными картами они являются составной частью картографического обеспечения имеющихся и создаваемых систем управления, информационно-расчетных систем.

Пространственные модели местности позволяют решить следующие задачи: 

- общую оценку местности; 

- изучение и оценку свойств местности и отдельных наземных и подземных (подводных) объектов;

- ориентирование на местности;

- отображение данных о местности и обстановке;

- моделирование обстановки;

- решение информационных, расчетных и навигационных задач;

- обучение пользователей на тренажерах реального времени;

- проведение учебных занятий, тренировок и других мероприятий, связанных с подготовкой специалистов для решения задач на местности;

- повышение качества создаваемых пространственных моделей местности;

- информационную совместимость различных систем управления и навигации, геоинформационных систем и тренажеров.

Область применения – для организаций и предприятий независимо от форм собственности и подчинения, которые занимаются сбором, систематизацией, анализом, обработкой и передачей пространственных данных, созданием и применением пространственных моделей местности, организацией баз и банков пространственных данных. Пространственная модель местности: Наглядное и измеримое трехмерное изображение земной поверхности на электронных средствах отображения информации, воспроизведенное в соответствии с заданными условиями наблюдения (обзора) на основе цифровой информации о местности (электронных карт, цифровых моделей местности), полученной с географических карт, кадастровых планов и космоаэрофотографических материалов, рельефных карт и видеоизображений.

Пространственная модель местности может быть представлена в виде двух изображений на экранах мониторов, обеспечивающих объемное (стереоскопическое) наблюдение участка местности и объектов (наземных, подземных, подводных).

Требования к пространственным моделям местности: должны обеспечивать

- возможность наглядного представления трехмерного образа местности с топологическими связями и характеристиками в зависимости от времени суток, года и обстановки на экранах индивидуального и коллективного пользования;

- возможность наглядного зрительного восприятия рельефа, пространственных форм, размеров и положения наземных и подземных объектов местности, коммуникаций;

- читаемость и распознаваемость элементов и объектов местности;

- многоплановость изображения элементов и объектов местности;

- измеримость изображения;

- визуальную оценку взаимного пространственного расположения объектов.

Математическая основа моделей местности (проекция, масштаб) должна обеспечивать получение наглядного и топографически точного без разрывов изображения местности в определенном масштабе.

Содержание модели местности должно включать следующие элементы: рельеф, гидрографию, населенные пункты, сельскохозяйственные, промышленные и социально-культурные объекты, дорожную сеть, растительный покров и грунты, границы, подписи названий объектов местности и их характеристик, в том числе подземных (подводных) объектов и топологических связей между ними с необходимыми характеристиками. 

ARIMA (англ. autoregressive integrated moving average) — интегрированная модель авторегрессии — скользящего среднего — модель и методология анализа временных рядов, иногда называемых моделями (или методологией) Бокса-Дженкинса. Являются расширением моделей ARMA для нестационарных временных рядов, которые можно сделать стационарными взятием разностей некоторого порядка от исходного временного ряда (так называемые интегрированные или разностно-стационарные временные ряды). Модель означает, что разности временного ряда порядка подчиняются модели ARMA(p, q). Эти модели используются при работе с временными рядами для более глубокого понимания данных или предсказания будущих точек ряда. Обычно модель упоминается, как ARIMA(p,d,q), где p,d и q — целые неотрицательные числа, характеризующие порядок для частей модели (соответственно авторегрессионной, интегрированной и скользящего среднего).

Методология ARIMA (Бокса-Дженкинса)

Подход ARIMA к временным рядам заключается в том, что в первую очередь оценивается стационарность ряда. Различными тестами выявляются наличие единичных корней и порядок интегрированности временного ряда (обычно ограничиваются первым или вторым порядком). Далее при необходимости (если порядок интегрированности больше нуля) ряд преобразуется взятием разности соответствующего порядка и уже для преобразованной модели строится некоторая ARMA-модель поскольку предполагается, что полученный процесс является стационарным, в отличие от исходного нестационарного процесса (разностно-стационарного или интегрированного процесса порядка d).

Модели ARFIMA

Теоретически порядок интегрированности d временного ряда может быть не целой величиной, а дробной. В этом случае говорят о дробно-интегрированых моделях авторегрессии-скользящего среднего (ARFIMA, AutoRegressive Fractional Integrated Moving Average). Для понимания сущности дробного интегрирования необходимо рассмотреть разложение оператора взятия d-ой разности в степенной ряд по степеням лагового оператора для дробных d (разложение в ряд Тейлора):

Используется большое количество вариаций модели ARIMA. Например, если исследуются несколько рядов, то можно трактовать как векторы. Иногда в модели может иметься сезонный фактор. Примером может послужить модель объёма трафика за день. На выходных поведение ряда будет заметно отличаться от рабочих дней. В этом случае вместо того, чтобы наращивать порядки скользящего среднего и авторегрессионной части модели, лучше прибегнуть к модели сезонного авторегрессионного скользящего среднего (SARIMA). Если имеется некоторая долгосрочная зависимость, параметр d может быть заменён нецелыми значениями, приводя к авторегрессионному дробноинтегрированному процессу скользящего среднего (FARIMA или ARFIMA).

ARIMA применяется для прогнозирования объемов инвестирования в факторы производства, такие как производственный и человеческий капитал региональной экономики.