Методы расчета показателей надежности СЖАТ. Особенности надежности и безопасности сжат

• Название: Особенности надежности и безопасности сжат
• Дата: 02.03.2022
• Размер: 434.34 Kb.
• Имя файла: Методы расчета показателей надежности СЖАТ.docx
• Тип: Документы; #380531
• страница: 4 из 7

РАСЧЕТ ПОКАЗАТЕЛЕЙ НАДЕЖНОСТИ ВОССТАНАВЛИВАЕМЫХ СИСТЕМ МЕТОДОМ МАРКОВСКИХ ПРОЦЕССОВ

ИСХОДНЫЕ ДАННЫЕ

Вариант № 5

варианта ik =  = 5∙10−4 1/ч,

ik =  = 2 1/ч)

РАСЧЕТЫ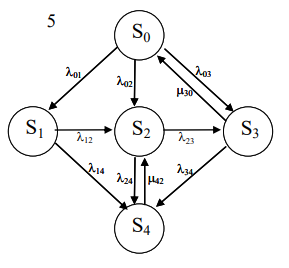

Рисунок 2. Граф состояний схемы.

Исходя из графа, система может находиться в одном из четырех состояний:

0 – исправное состояние;

1 – первое работоспособное состояние, отказал первый элемент, второй и третий – исправны;

2 – второе работоспособное состояние, отказал второй элемент, первый и третий – исправны;

3 – третье работоспособное состояние, отказал третий, первый и второй – исправны;

4 – неработоспособное состояние, отказали последовательно три элемента и находятся в состоянии ремонта.

Составим систему уравнений Колмогорова для финальных вероятностей нахождения во всех состояниях.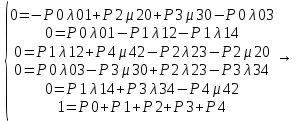





Система состоит из шести уравнений, пять неизвестных, значит можно путем подстановки выразить каждую переменную:

P₁=0,5P₀

P₃=0,002P₀-P₂=0,001P₀

P₂=0,001P₀

P₄=0,001P₁+0,001P₃=0,0005P₀

Подставим получившиеся значения в шестое уравнение:

1=P₀+P₁+P₂+P₃+P₄

1=P₀+0,5P₀+0,001P₀+0,001P₀+0,0005P₀

1=1,5025P₀

P₀=0,366

P₁=0,333

P₂=0,000666

P₃=0,000666

P₄=0,000333

Вероятность отказа системы:

Q_C=P₄=0,000333

Вероятность безотказной работы:

P_C=1-Q_C=1-0,000333=0,99967

Время наработки на отказ:

T_ср= 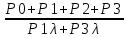= =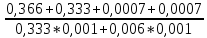3028,2 ч.

Интенсивность отказов:

λ_c=1/ T_ср=1/3028,2 =0,0003 1/ч.

Среднее время восстановления:

T_в= 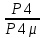= =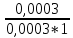1

Коэффициент готовности:

К_г= 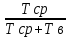= =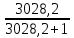0,999

Для нахождения среднего времени безотказной работы выполним преобразование Лапласа для уравнений Колмогорова с учетом начальных условий: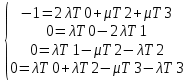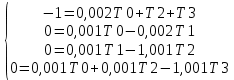

→

Система состоит из четырех уравнений, 3 неизвестных, значит можно путем подстановки выразить каждую переменную:

T₀=2T₁

T₂=0,0009T₁

T₃=0,0019T₁

Полученные результаты подставим в первое уравнение:

-1=-0,002T₀+T₂+T₃

-1=-0,004T₁+0,0009T₁+0,0019T₁

-1=-0,001T₁

T₁=1000 ч.

T₀=2000 ч.

T₂=0,9 ч.

T₃=1,9 ч.

Среднее время безотказной работы системы:

T_от=T₀+T₁+T₂+T₃=2000+1000+0,9+1,9=3002,8 ч.

По исходному графу, представленному на рисунке 3, известными интенсивностями отказов λ_ik и интенсивностям восстановления μ_ik, были найдены показатели надежности для восстанавливаемых систем, используя при этом метод марковских процессов:

• 
  вероятность отказа системы: Q_с=0,000333;
  
• 
  вероятность безотказной работы: P_с=0,99967;
  
• 
  среднее время наработки на отказ: Т_ср=3028,2 ч.;
  
• 
  интенсивность отказов системы: λ_c=0,0003 1/ч.;
  
• 
  среднее время восстановления: T_в=1 ч.;
  
• 
  коэффициент готовности: К_г=0,999;
  
• 
  среднее время безотказной работы: T_от= 3002,8 ч.