Методы расчета показателей надежности СЖАТ. Особенности надежности и безопасности сжат
 Скачать 434.34 Kb. Скачать 434.34 Kb.
|
МЕТОДЫ РАСЧЕТА ПОКАЗАТЕЛЕЙ НАДЕЖНОСТИ СЖАТВ курсовой работе рассмотрены следующие методы расчёта показателей надежности:статистическая оценка показателей надежности;расчет надежности комбинационных схем;расчет показателей надежности восстанавливаемых систем методом марковских процессов;структурный метод расчета надежности;топологический метод расчета надежности резервированных систем;расчет эксплуатационной надежности СЖАТ.Основные показатели надежности можно разбить на две группы: показатели, характеризующие надежность невосстанавливаемых систем; показатели, характеризующие надежность восстанавливаемых систем. Невосстанавливаемыми называются такие системы, для которых в рассматриваемой ситуации проведение восстановления работоспособного состояния не предусмотрено в нормативно-технической и (или) конструкторской документации. Если происходит отказ такой системы, то выполняемая операция будет сорвана, и ее необходимо начинать вновь в том случае, если отказ можно устранить Восстанавливаемыми называются такие системы, для которых в рассматриваемой ситуации проведение восстановления работоспособного состояния предусмотрено в нормативно-технической и (или) конструкторской документации. Если произойдет отказ такой системы, то он вызовет прекращение функционирования только на период устранения отказа. СТАТИСТИЧЕСИЕ ОЦЕНКИ ПОКАЗАТЕЛЕЙ НАДЕЖНОСТИПОСТРОЕНИЕ ФУЕКЦИИ РАСПРЕДЕЛЕНИЯ И ФУНКЦИИ ПЛОТНОСТИ РАСПРЕДЕЛЕНИЯ ПО СТАТИСТИЧЕСКОЙ ВЫБОРКЕИСХОДНЫЕ ДАННЫЕ Вариант № 5,16
Таблица 1. Исходные данные. Статистический ряд для данной выборки представлен в таблице 2, там же показан номер интервала, в который попадает определенное значение. Таблица 2. Статистический ряд.
В таблице 1 представлена выборка из n=30 значений, характеризующих количество дней безотказной работы. Для дальнейших расчетов необходимо перейти от дней к часам. Проведем статистическую оценку закона распределения случайной величины. В первую очередь определим диапазон значений случайной величины – размах. R = tmax - tmin = (13,10 – 0,08) 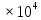 = 13,02 = 13,02 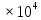 часов. часов.Диапазон R необходимо разбить на интервалы Δt: Δt = 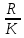 = = 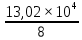 = = 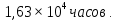 где K – количество интервалов. Частота попаданий в i интервал определяется по формуле: 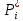 = = 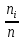 Статистическую плотность вероятности времени безотказной работы определим по формуле: 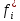 = = 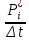 Значения частоты попаданий в i интервал и плотность распределения приведены в таблице 3. Таблица 3. Результаты расчетов.
Наглядное представление о законе распределения случайной величины t дают статистические графики: 1) полигон; 2) гистограмма; 3) статистическая функция распределения. Для рассматриваемого варианта графики имеют следующий вид: Среднее время наработки до отказа найдем по формуле: Tср = 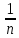 ∑Ti = ∑Ti =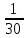 × 97,61 × 97,61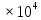 = 3,25 = 3,25 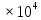 ч. ч.Интенсивность отказов равна: λ = 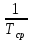 = = 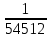 =3,07× 10-5 1/ч. =3,07× 10-5 1/ч.Используя полученное значение интенсивности отказов λ, найдем значения частоты отказов для заданных значений времени наработки t. Эти значения представлены в таблице 3. Далее, найдем теоретическое число попаданий в i-й интервал: 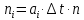 Значения теоретического числа попаданий в i-й интервал 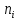 представлено в 8-й строчке таблицы 3. представлено в 8-й строчке таблицы 3. Далее, найдем значения 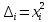 меры расхождения между теоретическими числами меры расхождения между теоретическими числами 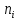 и экспериментальными и экспериментальными 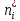 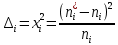 Найдем Δ путем суммирования всех значений Δi: Δ = ∑Δi = 0,03+0,52+0,16+0,84+1,38+0,93+0,57+1,28 = 5,71 Число степеней свободы: r = K – s = 8-2 = 6 С помощью полученных значений r и Δ определяем, что γ = 0,41. Это значение превышает порог 0,3÷0,4 что свидетельствует о согласии экспериментальных данных с гипотезой об экспоненциальном законе распределения времени наработки до отказа. СТАТИСТИЧЕСКАЯ ОЦЕНКА ПАРАМЕТРОВ НАДЕЖНОСТИ ВОССТАНАВЛИВАЕМЫХ УСТРОЙСТВИСХОДНЫЕ ДАННЫЕ Вариант № 10 Промежуток времени: Δt02 t1 = 10 мес. = 2520 часов; t2 = 20 мес. = 1116740 часов; t3 = 30 мес. = 21960 часов; N0 = 1000 шт.; n02 = 60 шт.; nв02 = 50 шт.; Вероятность безотказной работы: 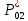 = = 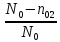 = = 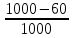 = 0,94 = 0,94Вероятность отказа: 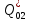 = 1 - = 1 - 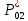 = 1 – 0,94 = 0,06 = 1 – 0,94 = 0,06Частота отказов: 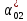 = = 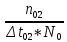 = = 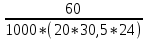 = 4,09*10-6 1/ч. = 4,09*10-6 1/ч.Интенсивность отказов: 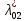 = = 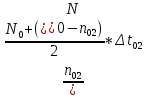 = = 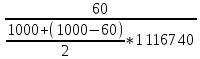 = 4,23*10-6 1/ч. = 4,23*10-6 1/ч.Параметр потока отказов: 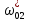 = = 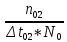 = = 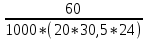 = 4,09*10-6 1/ч. = 4,09*10-6 1/ч.Вероятность восстановления: 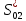 = = 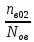 = = 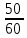 = 0,83 = 0,83Частота восстановления: 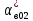 = = 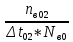 = = 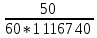 = 5,69*10-5 1/ч. = 5,69*10-5 1/ч.Интенсивность восстановления: 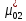 = = 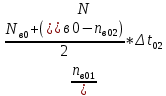 = = 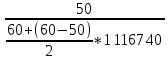 = 9,76*10-5 1/ч. = 9,76*10-5 1/ч.В результате статистической оценки параметров надежности восстанавливаемых систем были найдены параметры надежности устройств на промежутке времени: вероятность безотказной работы: 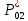 = 0,94; = 0,94;частота отказов: 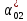 = 4,09*10-6 1/ч.; = 4,09*10-6 1/ч.;интенсивность отказов: 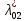 = 4,23*10-6 1/ч.; = 4,23*10-6 1/ч.;вероятность восстановления: 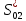 = 0,83; = 0,83;частота восстановления: 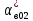 = 5,69*10-5 1/ч.; = 5,69*10-5 1/ч.;интенсивность восстановления: 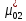 = 9,76*10-5 1/ч. = 9,76*10-5 1/ч. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

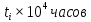
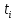 ,
,  1/час
1/час ,
,