Курсовая матлог Маи 1 курс. Курсовая работа. Отчет по курсовой работе по учебной дисциплине Математическая логика

• Название: Отчет по курсовой работе по учебной дисциплине Математическая логика
• Анкор: Курсовая матлог Маи 1 курс
• Дата: 11.05.2021
• Размер: 340.82 Kb.
• Имя файла: Курсовая работа.docx
• Тип: Отчет; #203816
• страница: 2 из 5

Матрицы:

Q = G H =Q (A,S);

A = X Y = {x0, x1, x2, x3, x4} {x0, x1, x2, x3, x4} = {x0, x1, x2, x3, x4};

Sx0 = Fx0 Px0 = {x0, x2, x4} {x2, x3} = {x0, x2, x3, x4};

Sx1 = Fx1 Px1 = {x1, x3} {x1, x3} = {x1, x3};

Sx2 = Fx2 Px2 = {x1, x2} {x1} = {x1, x2};

Sx3 = Fx3 Px3 = = ;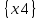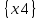

Sx4 = Fx4 Px4 = =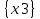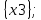

1. 
   Матрица смежности R ориентированного графа есть квадратная (nn) матрица R={rij} i,j=1..n, строки и столбцы которой соответствуют вершинам графа, а элементы матрицы rij – булевые переменные и равны соответственно: 1 если xjFxi ,то есть существует дуга (xi, xj), 0 если xjFxi , т.е. дуга (xi, xj) – не существует.
   

	x0	x1	x2	x3	x4
x0	1	0	1	1	1
x1	0	1	0	1	0
x2	0	1	1	0	0
x3	0	0	0	0	1
x4	0	0	0	1	0

R =

3.2. Матрица инцидентности А ориентированного графа есть прямоугольная матрица A={aik}, строки которой соответствуют вершинам графа, а столбцы - его ребрам. Тогда элементы матрицы aik будут равны:

0 – если вершина xi не является граничной точкой для ребра uk ;

+1 – если дуга uk заходит в вершину xi ;

1 – если дуга uk исходит из вершины xi

1 – если дуга является петлей Xi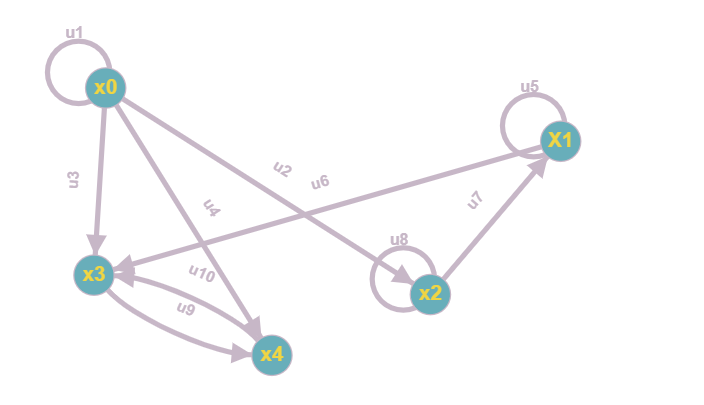

	U1	U2	U3	U4	U5	U6	U7	U8	U9	U10
X0	1	-1	-1	-1	0	0	0	0	0	0
X1	0	0	0	0	1	-1	+1	0	0	0
X2	0	+1	0	0	0	0	-1	1	0	0
X3	0	0	+1	0	0	+1	0	0	-1	+1
X4	0	0	0	+1	0	0	0	0	+1	-1

3.3. Матрица достижимости

Будем полагать, что вершина хj достижима из вершины хi, если существует хотя

бы один путь, ведущий из вершины хi к вершине хj.

Достижимость вершин в графе может быть задана с помощью матрицы

достижимости L={lij}, элементы которой lij равны:

1 если вершина хj достижима из хi , 0, если вершина хj недостижима из хi.
Матрица достижимости за один шаг (не более чем) (матрица смежности с единицами на диагонали):

	x0	x1	x2	x3	x4
x0	1	0	1	1	1
x1	0	1	0	1	0
x2	0	1	1	0	0
x3	0	0	0	1	1
x4	0	0	0	1	1

R^{1 =}

Матрица достижимости (не более чем) за 2 шага:

	x0	x1	x2	x3	x4
x0	1	1	1	1	1
x1	0	1	0	1	1
x2	0	1	1	1	0
x3	0	0	0	1	1
x4	0	0	0	1	1

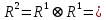Матрица достижимости за 3 шага:

	x0	x1	x2	x3	x4
x0	1	1	1	1	1
x1	0	1	0	1	1
x2	0	1	1	1	1
x3	0	0	0	1	1
x4	0	0	0	1	1

=

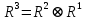Матрица достижимости за 4 шага:

	x0	x1	x2	x3	x4
x0	1	1	1	1	1
x1	0	1	0	1	1
x2	0	1	1	1	1
x3	0	0	0	1	1
x4	0	0	0	1	1