Курсовая матлог Маи 1 курс. Курсовая работа. Отчет по курсовой работе по учебной дисциплине Математическая логика
 Скачать 340.82 Kb. Скачать 340.82 Kb.
|
 Московский авиационный институт Московский авиационный институт(национальный исследовательский университет) Институт № 3 «Системы управления, информатика и электроэнергетика» Кафедра №304 «Вычислительные машины, системы и сети» Отчет по курсовой работе по учебной дисциплине «Математическая логика» на тему: «Графы» Группа: М30-107Б-20 Выполнил: Костанди Г.И. Почта студента: kostandi.gosha@yandex.ru Преподаватель: Владимир Ескин Задание для курсовой работы по графам Цель курсовой работы: освоение математического аппарата задания, анализа графовых моделей дискретных систем и решения ряда основных задач на графах. Индивидуальный вариант графов необходимо получить на сайте ws-dss.com (метод graph_generator). Порядок выполнения: 1. Описать исходные графы аналитически. 2. Построить аналитически и графически объединение, пересечения, разность графов G (X, F) и H (Y, P), дополнение графа G по отображению до графа H и до универсального графа L. 3. Для графа S=GH построить матрицы смежности, инцидентности, достижимости, конденсацию графа. Определить все базовые множества графа. 4. Для графа S = GH построить Гамильтонов (если он не существует, то дополнить граф необходимыми дугами, обозначив их на графе). Гамильтонов путь построить - с использованием алгоритма Фаулкса. 5. Получить из графа S неориентированный граф путем замены всех ориентированных ребер, на неориентированные. Лишние (параллельные) ребра удалить. Найти в полученном графе Эйлеров путь. Если он не существует, то дополнить граф необходимыми звеньями, обозначив их на графе. Полученные результаты сравнить с результатами расчетов на ЭВМ (методы hamiltonian_path – для ориентированного графа и eulerian_path – только для неориентированного графа). 6. Определение связности графа. 6.1. Для заданного с помощью матрицы смежности неориентированного графа найти связные компоненты, используя алгоритм Фаулкса. 6.2. Представить заданный граф графически. 6.3. Найти связные компоненты в графе, используя метод graph_connectivity на сайте ws-dss.com. Сравнить полученные результаты. 7. Для рассмотренных задач: поиск Гамильтонова пути; поиск Эйлерова пути; определение связности графа; поиск базовых множеств, предложить содержательное (предметное) описание подходящей технической задачи. 8. Оформить отчет. Отчет должен содержать содержание, задание, ход выполнения работы с пояснениями, выводы по работе, список используемой литературы. Индивидуальный вариант графов 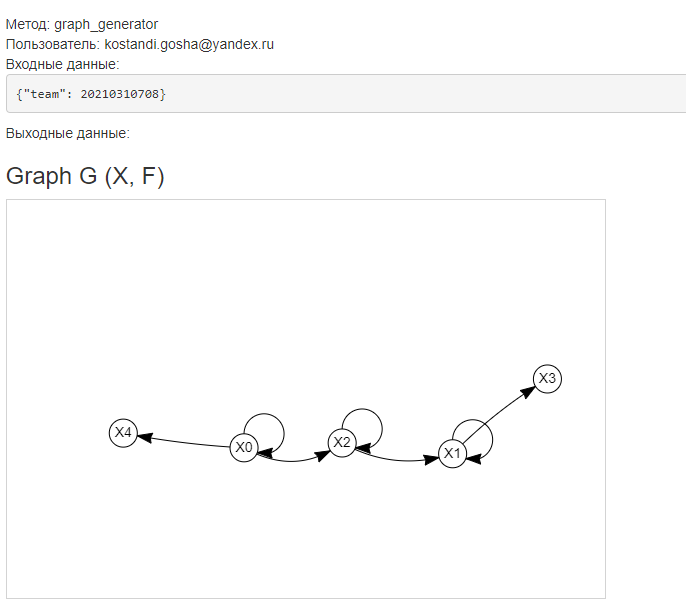 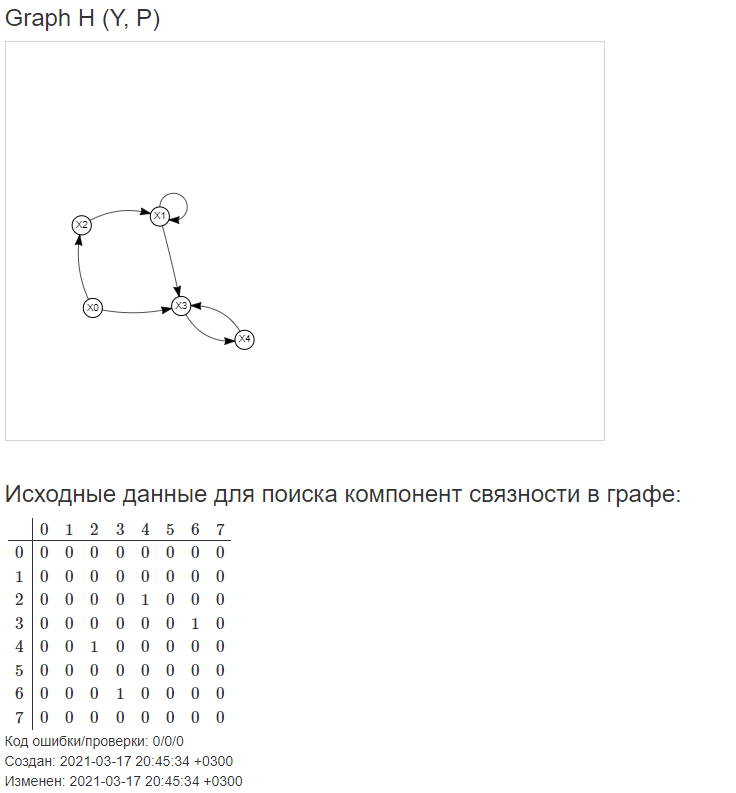  №1. Описание исходных графов аналитически. Ориентированный граф G = (X, F) есть совокупность двух объектов: множества вершин X={x1,x2,…,xn}и отображения F={Fxi 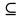 X}, характеризующего связи между вершинами. Отображение Fxi указывает – к каким элементам множества X ведут дуги, X}, характеризующего связи между вершинами. Отображение Fxi указывает – к каким элементам множества X ведут дуги,исходящие из элемента xi (i = 1,..,n). Граф G(X,F) 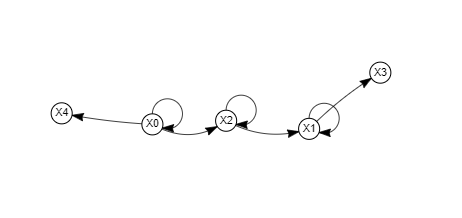 X = {x0, x1, x2, x3, x4} Fx0 = {x0, x2, x4} Fx1 = {x1, x3} Fx2 = {x1, x2} Fx3 =  Fx4 =  Граф H (Y,P) 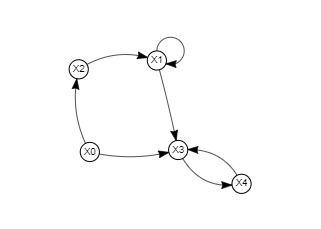 Y = {x0, x1, x2, x3, x4} Px0 = {x2, x3} Px1 = {x1, x3} Px2 = {x1} Px3 = 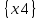 Px4 = 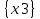 №2. Построение графически и аналитически. Объединение Q = G  H =Q (A,S); H =Q (A,S);A = X  Y = {x0, x1, x2, x3, x4} Y = {x0, x1, x2, x3, x4}  {x0, x1, x2, x3, x4} = {x0, x1, x2, x3, x4}; {x0, x1, x2, x3, x4} = {x0, x1, x2, x3, x4};Sx0 = Fx0  Px0 = {x0, x2, x4} Px0 = {x0, x2, x4}  {x2, x3} = {x0, x2, x3, x4}; {x2, x3} = {x0, x2, x3, x4};Sx1 = Fx1  Px1 = {x1, x3} Px1 = {x1, x3}  {x1, x3} = {x1, x3}; {x1, x3} = {x1, x3};Sx2 = Fx2  Px2 = {x1, x2} Px2 = {x1, x2}  {x1} = {x1, x2}; {x1} = {x1, x2};Sx3 = Fx3  Px3 = Px3 =   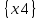 = = 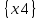 ; ;Sx4 = Fx4  Px4 = Px4 =  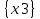 = = 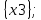 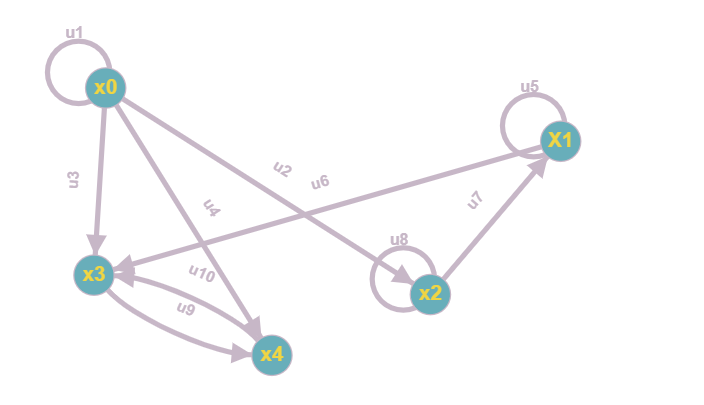 Пересечение Q = G 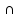 H =Q (A,S); H =Q (A,S);A = X 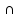 Y = {x0, x1, x2, x3, x4} Y = {x0, x1, x2, x3, x4} 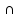 {x0, x1, x2, x3, x4} = {x0, x1, x2, x3, x4}; {x0, x1, x2, x3, x4} = {x0, x1, x2, x3, x4};Sx0 = Fx0 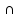 Px0 = {x0, x2, x4} Px0 = {x0, x2, x4} 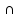 {x2, x3} = {x2}; {x2, x3} = {x2};Sx1 = Fx1 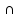 Px1 = {x1, x3} Px1 = {x1, x3}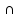 {x1, x3} = {x1, x3}; {x1, x3} = {x1, x3};Sx2 = Fx2 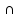 Px2 = {x1, x2} Px2 = {x1, x2} 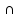 {x1} = {x1}; {x1} = {x1};Sx3 = Fx3 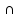 Px3 = Px3 =  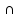 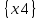 = =  ; ;Sx4 = Fx4 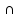 Px4 = Px4 = 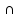 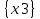 = =  ; ;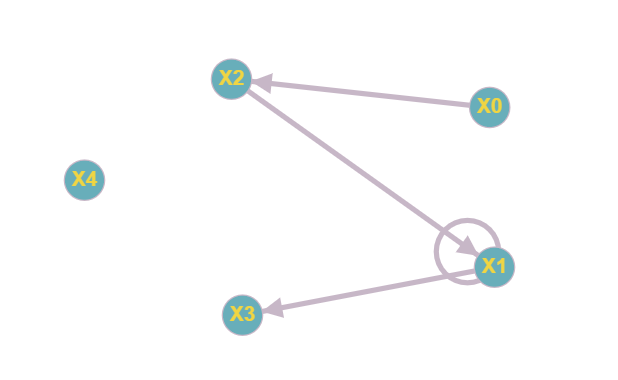 Разности графов G(X,F) и H (Y,P) Q(A,S) = G(X, F) \ H(Y, P) = Q(Х, (Fх \ Pх)) Sx0 = Fx0 \ Px0 = {x0, x2, x4} 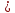 {x2, x3} = {x0, x4}; {x2, x3} = {x0, x4};Sx1 = Fx1 \ Px1 = {x1, x3} 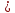 {x1, x3} = {x1, x3} =  ; ;Sx2 = Fx2 \ Px2 = {x1, x2} 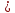 {x1} = {x2}; {x1} = {x2};Sx3 = Fx3 \ Px3 =  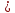 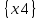 = =  ; ;Sx4 = Fx4 \ Px4 =  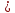 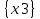 = = ; ;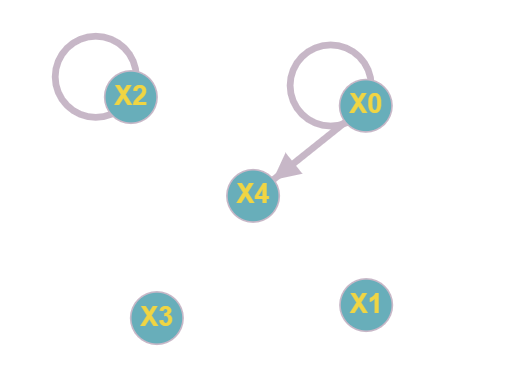 дополнение графа G по отображению до графа H и до универсального графа L Дополнение графа G по отображению до графа H невозможно т.к. не выполняется условие  . .Универсальным графом L будем считать объединение G и H (L = G  H = L(A, S)) H = L(A, S))Q = Q (A, S \ F) = Q(A, B) A = X  Y = {x0, x1, x2, x3, x4} Y = {x0, x1, x2, x3, x4}  {x0, x1, x2, x3, x4} = {x0, x1, x2, x3, x4}; {x0, x1, x2, x3, x4} = {x0, x1, x2, x3, x4};Ax0 = Sx0 \ Fx0 = {x0, x2, x3, x4}  {x0, x2, x4} = {x3}; {x0, x2, x4} = {x3};Ax1 = Sx1 \ Fx1 = {x1, x3}  {x1, x3} = {x1, x3} =  Ax2 = Sx2 \ Fx2 = {x1, x2}  {x1, x2} = {x1, x2} =  Ax3 = Sx3 \ Fx3 = 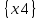 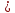  = {x4} = {x4}Ax4 = Sx4 \ Fx4 = 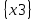 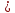  = {x3} = {x3}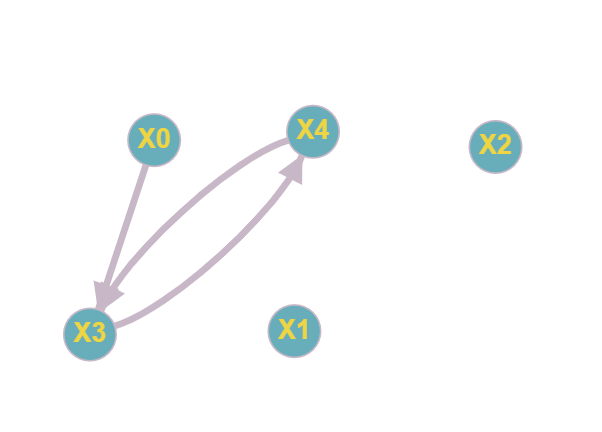 №3. Для графа S=G⋃H построить: |
