Курсовая матлог Маи 1 курс. Курсовая работа. Отчет по курсовой работе по учебной дисциплине Математическая логика
 Скачать 340.82 Kb. Скачать 340.82 Kb.
|
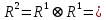 8. Проверяем условие равенства R1и 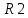 . Так как они не равны, переходим к п.9 . Так как они не равны, переходим к п.99. Проверяем условие равенства всех элементов матрицы единице. Так как оно не выполняется, то возвращаемся к п.4. 4. Рассмотрим матрицу R2. Вершина x0, является начальной вершиной гамильтонова пути на данном цикле вычислений. 5. Вычеркиваем столбец и строку x0. Оставшаяся матрица 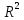 имеет вид имеет вид
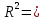 6. N=2+1=3. 7. Производим умножение R2  R1 = R3 R1 = R3
R3 = 8. R3 не равно R2. 9. Проверяем условие равенства всех элементов матрицы единице. Так как оно не выполняется, то возвращаемся к п.4. 4. Рассмотрим матрицу R3. Вершина x2, является начальной вершиной гамильтонова пути на данном цикле вычислений. 5. Вычеркиваем столбец и строку x2. Оставшаяся матрица 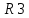 имеет вид: имеет вид:
R3 = 6. N=3+1=4. 7. Производим умножение R3  R1 = R4 R1 = R4
R4 = 8. R4 = R3. 10. Матрицу Rb получаем возвращением строк и столбцов, вычеркнутых в п. 5
11. Перегруппируем строки и столбцы матрицы Rb так, чтобы все нули были расположены под главной диагональю, а единицы - над ней: Получаем матрицу Rc.
Таким образом, получили 4 класса эквивалентности: - в первый класс входит вершина x0; - во второй – вершина x2, в третий – вершина x1, в четвертый – x3, x4. Т.е. в гамильтоновом пути вершина x0 предшествуют вершине x2, вершина x2 предшествует вершине x1, вершина x1 предшествует вершинам x3, x4. Всего возможно 1! ∙ 4! ∙1! ∙ 1! = 24 вариантов следования вершин. С учетом необходимости выполнения условий связи, определение гамильтонова пути становится достаточно простым. В данном примере получим следующий ГП: 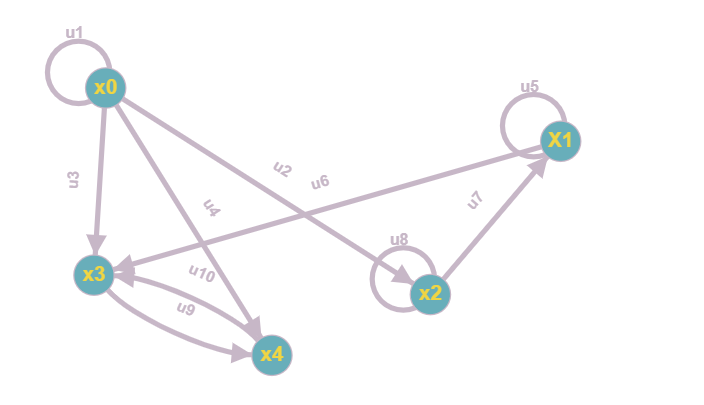 x0x2x1x3x4 Сразу же проверим ответ на https://ws-dss.com/: Метод: hamiltonian_path Пользователь: kostandi.gosha@yandex.ru Входные данные: { "graf": { "0": ["0","2","3","4"], "1": ["1","3"], "2": ["1","2"], "3": ["4"], "4": ["3"] } } Выходные данные: Гамильтонов путь: 0-2-1-3-4 Код ошибки/проверки: 0/0/0 Создан: 2021-04-21 09:59:34 +0300 Изменен: 2021-04-21 09:59:34 +0300  Вывод: полученные результаты совпали с ожидаемыми. №5. Найти Эйлеров путь в неориентированном графе S=G⋃H. Одна из важных задач теории графов заключается в нахождении пути (маршрута), содержащего по одному разу все ребра графа. Этот путь называется эйлеровым путем (ЭП) или эйлеровой линией в графе, а задачу его нахождения называют задачей Эйлера. Графы, на которых существуют замкнутые эйлеровы линии, называют эйлеровыми графами. Построим матрицу смежности для неориентированного графа S: Матрица смежности для ориентированного графа:
R = матрица смежности для неориентированного графа:
|
