Курсовая матлог Маи 1 курс. Курсовая работа. Отчет по курсовой работе по учебной дисциплине Математическая логика

• Название: Отчет по курсовой работе по учебной дисциплине Математическая логика
• Анкор: Курсовая матлог Маи 1 курс
• Дата: 11.05.2021
• Размер: 340.82 Kb.
• Имя файла: Курсовая работа.docx
• Тип: Отчет; #203816
• страница: 3 из 5

=

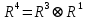Так как R4 = R3, следовательно, искомая матрица достижимости равна:

	x0	x1	x2	x3	x4
x0	1	1	1	1	1
x1	0	1	0	1	1
x2	0	1	1	1	1
x3	0	0	0	1	1
x4	0	0	0	1	1

R3 =

3.4. Конденсация графа

Матрица контрдостижимости Q ориентированного графа может

быть получена путѐм транспонирования матрицы достижимости, то есть:

Q = L ^T.

	x0	x1	x2	x3	x4
x0	1	0	0	0	0
x1	1	1	1	0	0
x2	1	0	1	0	0
x3	1	1	1	1	1
x4	1	1	1	1	1

Q =


Под сильной компонентой (СК) графа G(X,F) будем понимать подграф G’=СК

графа G максимальной размерности (максимальное число вершин), являющийся сильно

связным графом, который не содержится в любом другом сильно связном подграфе графа

G.

Для нахождения сильных компонент графа G произведѐм поэлементное

логическое перемножение (●) матриц достижимости L и контрдостижимости Q . В

результате получим матрицу СК=L●Q.

	x0	x1	x2	x3	x4
x0	1	0	0	0	0
x1	0	1	0	0	0
x2	0	0	1	0	0
x3	0	0	0	1	1
x4	0	0	0	1	1

СК =

В матрице СК можно увидеть четыре сильные компоненты это x1* = {x0}, x2*={x1}, x3* = {x2}, x4* = {x3, x4}. На этих сильных компонентах, как на вершинах, может быть построен новый граф S*(X*,F*), который называется конденсацией графа S.

X* = {x1*, x2*,x3*,x4*}

F*x1* = {x3*, x4*}

F*x2* = {x4*}

F*x3* = {x2*}

F*x4* = ∅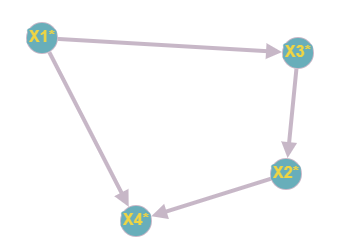



3.5 Базовые множества графа S=G⋃H

База B графа G=(X,F) есть множество B вершин графа G, из которых достижима любая вершина графа и которое является минимальным в том смысле, что не существует такого подмножества множества B, обладающего таким же свойством достижимости.
Из конденсации графа видно, что B = x1* = {x0} является базовым множеством графа.
Из матрицы достижимости мы так же можем найти базовые множества графа:

	x0	x1	x2	x3	x4
x0	1	1	1	1	1
x1	0	1	0	1	1
x2	0	1	1	1	1
x3	0	0	0	1	1
x4	0	0	0	1	1

Так же на данной матрице видно, что из x0 можно достигнуть любую другую вершину, а из остальных вершин достигнуть x0 нельзя, что подтверждает утверждение, что базовым множеством является B = {x0}

№4. Для графа S = G⋃H построить Гамильтонов путь.

Гамильтонов путь в графе – это путь, проходящий через все вершины графа, причем каждая вершина встречается в нем только один раз. Если этот путь замкнут, то говорят о гамильтоновом цикле.
Для решения задачи воспользуемся алгоритмом Фаулкса.
Q = G H =Q (A,S);

A = X Y = {x0, x1, x2, x3, x4} {x0, x1, x2, x3, x4} = {x0, x1, x2, x3, x4};

Sx0 = Fx0 Px0 = {x0, x2, x4} {x2, x3} = {x0, x2, x3, x4};

Sx1 = Fx1 Px1 = {x1, x3} {x1, x3} = {x1, x3};

Sx2 = Fx2 Px2 = {x1, x2} {x1} = {x1, x2};

Sx3 = Fx3 Px3 = = ;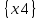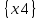

Sx4 = Fx4 Px4 = =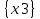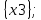

1. 
   Зададим номер цикла N = 1.
   
2. 
   Составим ориентированный граф (возьмем из задачи №2), соответствующий S=G⋃H.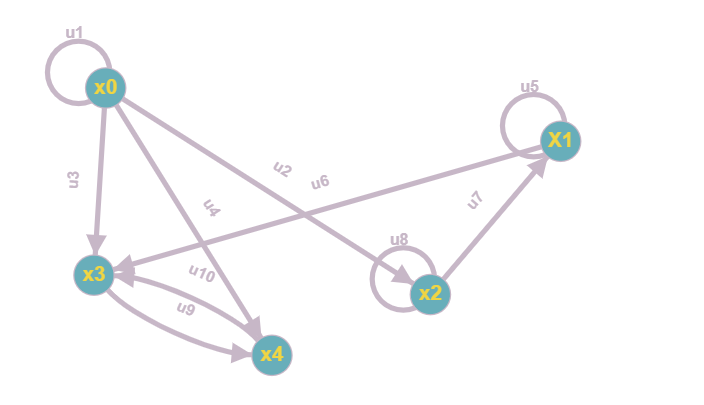
   

3. 
   Составим матрицу R1 достижимости не более чем за один шаг (возьмем из задачи №3).
   

	x0	x1	x2	x3	x4
x0	1	0	1	1	1
x1	0	1	0	1	0
x2	0	1	1	0	0
x3	0	0	0	1	1
x4	0	0	0	1	1

R1=


4. Проверим матрицу R1 на наличие начальной или конечной вершин ГП графа.

(Таких нет)

6. N=1+1=2.

7. Произведем булево умножение матриц R1 R1 = R2. Наличие 1 в матрице означает существование между соответствующими вершинами путей длиной меньшей или равной двум, а 0 - их отсутствие.

	x0	x1	x2	x3	x4
x0	1	1	1	1	1
x1	0	1	0	1	1
x2	0	1	1	1	0
x3	0	0	0	1	1
x4	0	0	0	1	1