Курсовая матлог Маи 1 курс. Курсовая работа. Отчет по курсовой работе по учебной дисциплине Математическая логика
 Скачать 340.82 Kb. Скачать 340.82 Kb.
|
|
R* = Заметим что степени вершин следующие: 3, 2, 2, 3, 2 т.е. Эйлеров путь в графе существует тогда и только тогда, когда граф связный и содержит не более двух вершин нечётной степени. Ввиду леммы о рукопожатиях, число вершин с нечётной степенью должно быть чётным. Причём, когда оно равно нулю, эйлеров путь вырождается в эйлеров цикл. 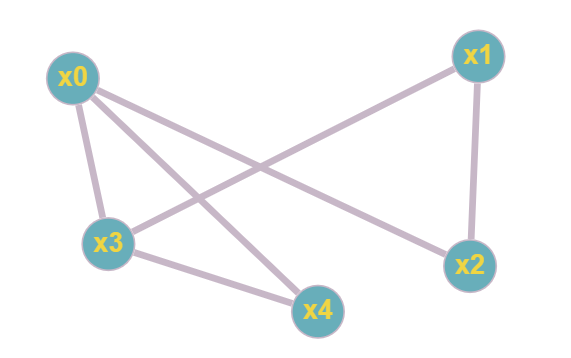 Начнем поиск Эйлерова пути для данного графа 0. k = 0. Выберем начальную вершину с номером 0, т.е. V0 = x0. Число непомеченных ребер S = 6 1. k = 1. С вершиной V0 = x0 связаны вершины x2, x3, x4 2. Число непомеченных ребер для вершины x0 S1 = 3. Следующей вершиной ЭП является вершина x2. Ребро x0-x2 помечается. Возвращаемся к п. 1 1. k = 2. Вершина x1. 2. S2 = 2 Вершина x1. Помечаем ребро x2-x1. Возвращаемся к п. 1 1. k = 3. Вершина x3. 2. S3 = 2 Вершина x3. Помечаем ребро x1-x3. Возвращаемся к п. 1 1. k = 4. Вершины x0, x4 2. S4 = 3 Вершина x0. Помечаем ребро x3-x0. Возвращаемся к п. 1 1. k = 5. Вершины x4 2. S5 = 1 Вершина x4. Помечаем ребро x0-x4. Возвращаемся к п. 1 1. k = 6. Вершина x3. 2. S6 = 3 Вершина x3. Помечаем ребро x4-x3. Возвращаемся к п. 1 1. k = 7. Вершин, связанных непомеченными ребрами, нет. 3. S7 = 0. В найденном цикле нет вершин, имеющих инцидентные непомеченные ребра. 4. Пропускаем т.к. у нас только один цикл. 5. Так как в этом пути нет вершин с непомеченными ребрами, то найденный путь является эйлеровым. Эйлеров путь: x0x2x1x3x0x4x3 Метод: eulerian_path Пользователь: kostandi.gosha@yandex.ru Входные данные: { "graf": [[0,2],[0,3],[0,4],[1,2], [1,3],[3,4]], "initial": 0 } Выходные данные: Вершины: 0,2,3,4,1 Ребра: (0,2), (0,3), (0,4), (1,2), (1,3), (3,4) Степени вершин: 3,2,3,2,2 Эйлеров путь сущетсвует Начальная вершина 0 Непомеченные ребра: (0,2), (0,3), (0,4), (1,2), (1,3), (3,4) Массив вершин ЭП [(0)] Помечаем ребро (0,2) Непомеченные ребра: (0,3), (0,4), (1,2), (1,3), (3,4) Массив вершин ЭП [(0,2)] Помечаем ребро (1,2) Непомеченные ребра: (0,3), (0,4), (1,3), (3,4) Массив вершин ЭП [(0,2,1)] Помечаем ребро (1,3) Непомеченные ребра: (0,3), (0,4), (3,4) Массив вершин ЭП [(0,2,1,3)] Помечаем ребро (0,3) Непомеченные ребра: (0,4), (3,4) Массив вершин ЭП [(0,2,1,3,0)] Помечаем ребро (0,4) Непомеченные ребра: (3,4) Массив вершин ЭП [(0,2,1,3,0,4)] Помечаем ребро (3,4) Непомеченных ребер нет Массив вершин ЭП [(0,2,1,3,0,4,3)] Эйлеров путь: (0, 2, 1, 3, 0, 4, 3) Код ошибки/проверки: 0/0/0 Создан: 2021-05-04 23:27:51 +0300 Изменен: 2021-05-04 23:27:51 +0300  Вывод: полученные результаты совпали с ожидаемыми. №6. Определение связности графа. 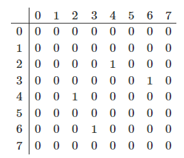 6.1. Для заданного с помощью матрицы смежности неориентированного графа найти связные компоненты, с помощью элементов алгоритма Фаулкса. На основании матрицы смежности R получим матрицу R1 достижимости не более чем за один шаг
Затем, в соответствии с алгоритмом Фаулкса, найдем матрицу RN путем булевского перемножения матриц до тех пор, пока не достигнем RN = RN-1.
Полученная матрица RN является матрицей достижимости графа. Она позволяет выявить связные подграфы и номера вершин, входящих в связные подграфы. Для этого необходимо в некоторой i - строке матрицы RN найти элементы rNij = 1, i, j = 1,…,n. Номера столбцов j, где rij = 1, и будут номерами вершин, входящих в связный подграф, включающий в себя i-ю вершину. Рассматривая последовательно все несовпадающие строки матрицы можно выявить все m связных подграфов исходного графа. G1 = {0} G2 = {1} G3 = {2,4} G4 = {3,6} G5 = {5} G6 = {7} G1, G2, G3 – являются связными компонентами рассматриваемого графа. 6.2. Представить заданный граф графически. 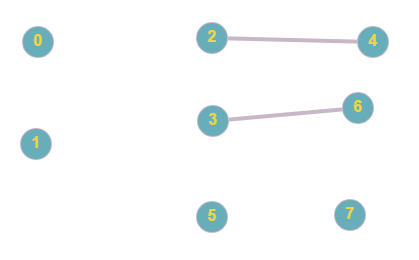 6.3. Найти связные компоненты в графе, используя метод graph_connectivity на сайте ws-dss.com. Сравнить полученные результаты. Метод: graph_connectivity Пользователь: kostandi.gosha@yandex.ru Входные данные: { "graf": { "0":[], "1": [], "2": ["4"], "3": ["6"], "4": [], "5": [], "6": [], "7": [] } } Выходные данные: Матрица смежности: 0 1 2 3 4 5 6 7 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 2 0 0 0 0 1 0 0 0 3 0 0 0 0 0 0 1 0 4 0 0 1 0 0 0 0 0 5 0 0 0 0 0 0 0 0 6 0 0 0 1 0 0 0 0 7 0 0 0 0 0 0 0 0 Матрица достижимости (число шагов 1) 0 1 0 0 0 0 0 0 0 1 0 1 0 0 0 0 0 0 2 0 0 1 0 1 0 0 0 3 0 0 0 1 0 0 1 0 4 0 0 1 0 1 0 0 0 5 0 0 0 0 0 1 0 0 6 0 0 0 1 0 0 1 0 7 0 0 0 0 0 0 0 1 Связные компоненты: 1) 0 2) 1 3) 2-4 4) 3-6 5) 5 6) 7 Код ошибки/проверки: 0/0/0 Создан: 2021-05-05 00:24:55 +0300 Изменен: 2021-05-05 00:25:26 +0300  №7. Примеры возможных практических задач: поиск Гамильтонова пути; Вы – курьер. Вам нужно развести заказы N клиентам. Так же начальство выдало вам самые оптимальные пути между клиентами в виде ориентированного графа. Причем нельзя заезжать на одну и ту же точку доставки дважды, т.к. будет перерасход бензина. поиск Эйлерова пути; Вы работаете торговым представителем фирмы. Начальник дал вам задание собрать за один день заявки четырех магазинов, которые находятся в деревнях. Ваша машина сломалась и вы вынуждены перемещаться между заказчиками на рейсовых автобусах, которые ходят один раз в день. Вам нужно выбрать такой маршрут, при котором будет затрачено меньшее количество финансов. ·определение связности графа; К вам обращаются с просьбой узнать - можно ли попасть из любого города в другой случайный город (в пределах нашей страны), используя только железную дорогу, к сожалению, вам дана только информация из какого города, в какой вы можете доехать за одну поездку. Поэтому вам придется проверять, связны ли все города одной системой железных дорог. ·поиск базовых множеств. Ваш друг только что узнал, что не все города в нашей стране соединены железной дорогой, и поэтому он просит вас разделить города на такие множества, что для городов внутри множества можно будет добраться друг к другу, используя систему железных дорог, а между множествами нет. Заключение В курсовом проекте были рассмотрены следующие вопросы: 1. Способы задания графов: изображение графа, способы численного представления графов 2. Виды графов и операции над ними 3. Нахождение конденсации и базовых множеств графа 4. Алгоритмы поиска Гамильтонова и Эйлерова пути в графе 5. Определение связности графа Вывод В ходе работы я освоил математический аппарат задания, анализа графовых моделей, дискретных систем и решения ряда основных задач на графах. Список используемой литературы 1. Босин П.Л., Булыгии В.С., Кулешов К.Г. Лабораторные работы но курсу «Основы теории конечных динамических систем», — М.: МАИ, 1985. 2. Булыгин B.C. Логические основы теории дискретных устройств: учеб. пособие. — M.: МАИ, 1983. 3. Булыгин B.C. Основы проектирования дискретных устройств АСУ: учеб. пособие. — M.: МАИ, 1982. 4. Просветов Г.И. Дискретная математика: задачи и решения: учебное пособие. — М.: БИНОМ. Лаборатория знаний,2008. – 222 с. 5. Кристофидес Н, Теория графов: Алгоритмический подход. - М.: Мир, 1978. 6. 9. Булыгин В.С., Ескин В.И. Лабораторные работы «Дискретная математика (логические функции, конечные автоматы, графы)», — М.: МАИ, 2011. |
