Бисяев. Бургали. Сводный отчет. Отчет по лабораторным и практическим работам по дисциплине Математическое моделирование, применение теории вероятностей и математической статистики в геологии
 Скачать 1.4 Mb. Скачать 1.4 Mb.
|
|
4.5 Построение и анализ диаграмм размаха Диаграммы размаха («ящик с усами») (Box and Whisker Plot или Box Plot) – это удобный способ визуального представления групп числовых данных через квартили. Прямые линии, исходящие из ящика, называются «усами» и используются для обозначения степени разброса (дисперсии) за пределами верхнего и нижнего квартилей. Диаграммы размаха, как правило, используются в описательной статистике и позволяют быстро исследовать один или более наборов данных в графическом виде. Несмотря на то, что в сравнении с гистограммой или графиком плотности, этот график может показаться примитивным, его преимущество – в экономии пространства, что особенно удобно при сравнении распределений между большим количеством групп или наборов данных [5]. Построение диапазонов значений выбранной переменной на диаграммах размаха проводится отдельно для групп наблюдений, определяемых значениями категорирующей или группирующей переменной. Вычисление центра (медиана или среднее) и статистики диапазонов или вариации (квартили, стандартные ошибки или стандартные отклонения) проводится для каждой группы наблюдений [1]. 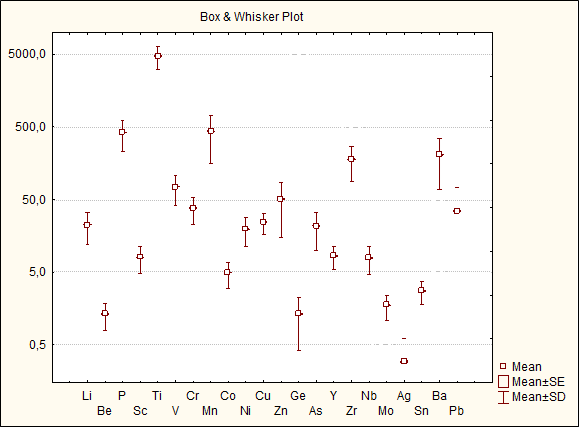 Рисунок 5 – Интервал разброса, среднее (медиана), 25-75% квартили содержания элементов в пробах участка Бургали Как видно из рисунка 5, элементный состав проб имеет широкий разброс значений. При этом отмечается преобладание элементов с четными порядковыми числами по таблице Д.И. Менделеева, чем с нечетными, что является яркой иллюстрацией закона Оддо-Гаркинса. Полученная диаграмма подтверждает закон Кларка-Вернадского, гласящего, что все элементы есть везде, речь может идти только о недостаточной чувствительности анализа, не позволяющего определить содержание того или иного элемента в изучаемой системе. 4.6 Корреляционный анализ Корреляционный анализ – раздел математической статистики, объединяющий практические методы исследования корреляционной связи между 2 и более случайными признаками или факторами. Функциональная связь, существующая между переменными (случайными величинами) проявляется в том, что одна из них определяется как функция от другой. Но между переменными существует связь другого рода, состоящая в том, что одна из переменных реагирует на изменение другой изменением своего закона распределения. Связь такого рода называется стохастическая. Проявляется она в случае, когда существуют общие случайные факторы, влияющие на обе случайные величины. Мерой зависимости между переменными является коэффициент корреляции, который имеет значения от -1 до +1. Если с увеличением значений одной переменной значения другой убывают, то коэффициент корреляции отрицательный. Когда переменные независимы, то коэффициент корреляции равен 0. Между переменными существует зависимость, если коэффициент корреляции не равен 0. Чем ближе значения r к 1, тем зависимость сильнее. Зависимость между переменными является линейной когда коэффициент корреляции достигает значений -1 и +1 [10]. В случае, когда не удается проверить гипотезу о соответствии эмпирического распределения определенному законы из-за малого количества данных (<30) или если распределение существенно отличается от нормального закона распределения, то для проверки гипотезы о наличии корреляционной связи используют непараметрический ранговый коэффициент корреляции Спирмена R. В моем случае почти все химические элементы с логнормальным распределением, следовательно, использую коэффициент Спирмена. Мною были построены матрица корреляционных связей химических элементов с уровнем значимости р < 0,05 (таблица 6). Рассмотрение матриц корреляционных связей химических элементов в пробах (таблица 7) позволяет говорить о следующем: наиболее сильная положительная корреляционная связь отмечается для пары Sn-W (0,69), наибольшая отрицательная – для пары Zn-Ba (-0,42). Таблица 7 – Матрица корреляционных связей химических элементов в пробах участка Бургали
|
