Бисяев. Бургали. Сводный отчет. Отчет по лабораторным и практическим работам по дисциплине Математическое моделирование, применение теории вероятностей и математической статистики в геологии
 Скачать 1.4 Mb. Скачать 1.4 Mb.
|
|
Примечание: жирным шрифтом и цветом выделены значимые корреляционные связи химических элементов на уровне вероятности 95%. Простой способ анализа корреляционной матрицы проводится с позиции теории графов. Графом называется геометрическая схема, включающая 2 и более точки конечного множества. Граф ассоциаций был построен по микроассоциации химических элементов As-Ag-Pb-Zn, предположительно связанной с оруденением, в ходе построения было обнаружено, что все элементы связаны значимой положительной связью (жирные линии), отрицательные связи вовсе не наблюдаются. 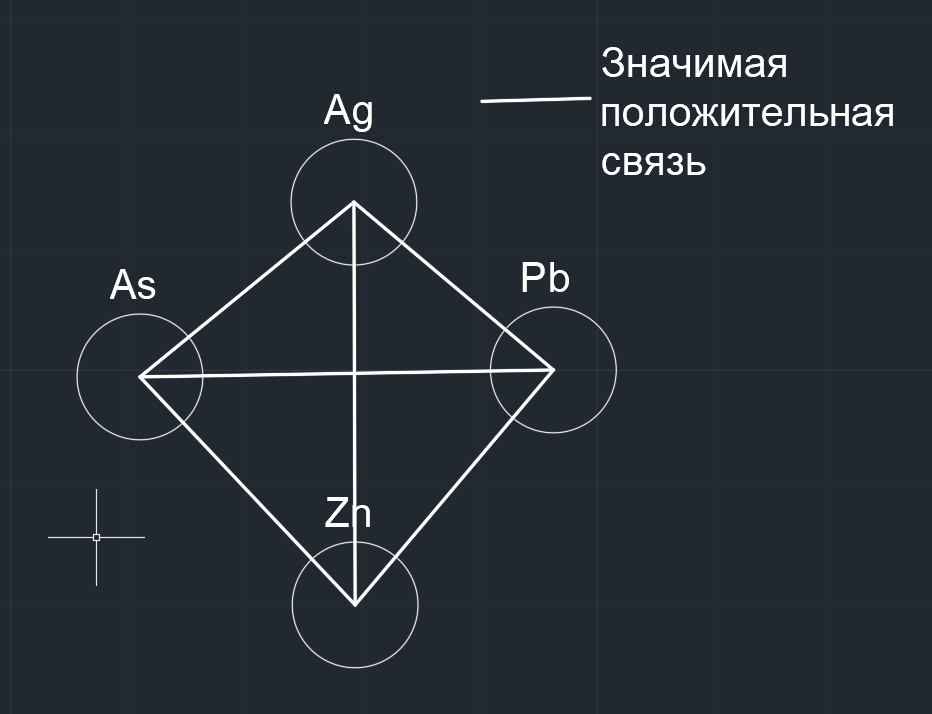 Рисунок 7 – Граф ассоциаций рудной минерализации Для графического отображения зависимости между двумя переменными проводится используется построение диаграмм рассеяния с помощью точек в двумерном пространстве. При сильной связи между переменными множество точек данных принимают определенную форму (например, ложится на прямую линию) [1]. Сильную, среднюю и слабую зависимости выделяют по тесноте, а по характеру – прямую (с увеличением значений одного параметра увеличиваются значения второго) и обратную (с увеличением значений одного, значения другого уменьшаются), по форме – линейную и нелинейную [5]. Мною построены 3 диаграмм рассеяния (рисунок 7-9). На рисунке 7 зависимость Ti-Zr линейная средняя, прямая. Зависимость между Li-Ge (рисунок 8) отрицательная. Между Li-Sn зависимость практически отсутствует (рисунок 9). 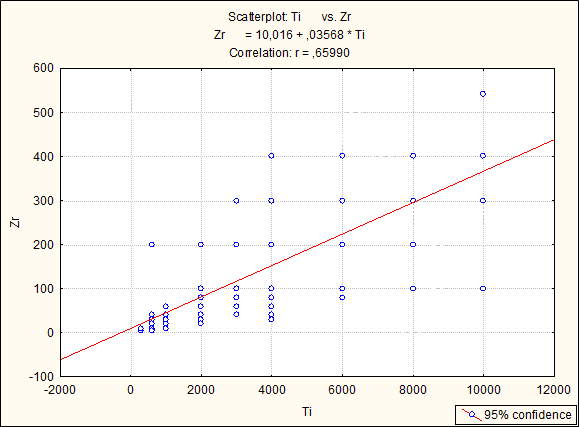 Рисунок 7 – Графики парной корреляционной связи между элементами Ti-Zr в пробах участка Бургали 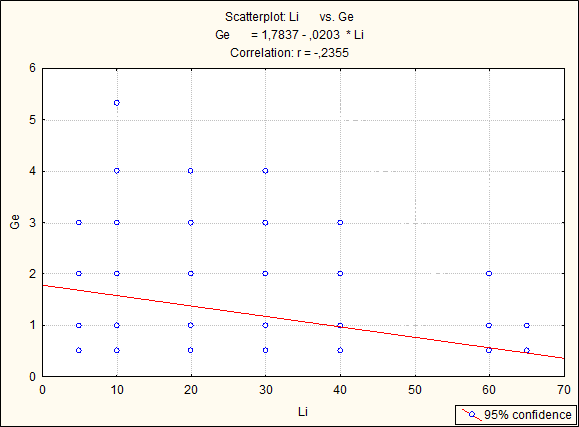 Рисунок 8 – Графики парной корреляционной связи между элементами Li-Ge в пробах участка Бургали 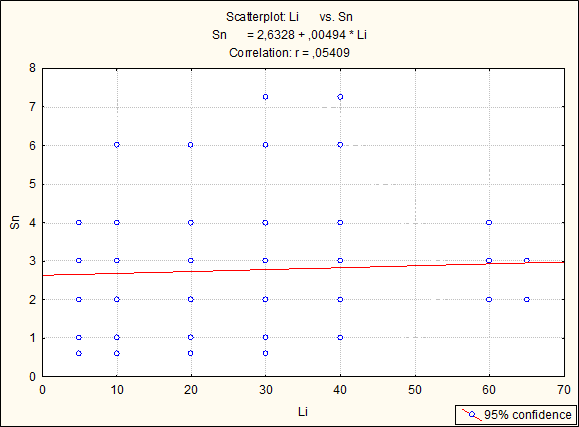 Рисунок 9 – Графики парной корреляционной связи между элементами Li-Sn в пробах участка Бургали 4.7 Кластерный анализ Кластерный анализ позволяет разбить исходную совокупность объектов на группы схожих, близких между собой объектов. Данные группы называют кластерами (таксонами). Существует несколько правил объединения кластеров. В нашем случае используется метод Варда. В методе Варда целевой функцией является внутригрупповая сумма квадратов отклонений, соответствующая сумме квадратов расстояний между каждой точкой (объектом) и средней по кластеру, содержащему этот объект. На каждом шаге объединяются такие два кластера, которые приводят к минимальному увеличению целевой функции, т.е. внутригрупповой суммы квадратов. Метод направлен на объединение близко расположенных кластеров. Графическое представление объединения групп элементов можно провести с помощью построения дендрограм. Дендрограмма (dendrogram) - древовидная диаграмма, содержащая n уровней, каждый из которых соответствует одному из шагов процесса последовательного укрупнения кластеров [2]. Построение проводилось с применением метода близости 1-r Пирсон. Как следует из рисунка 10 геохимические спектры микроэлементов в пробах образуют 3 крупных микроассоциаций {Zr-Ti-Nb-Ge-Ba-T-Sc, As-Ag-Pb-Zn, Cu-Ni-Co-Mn-Li}. 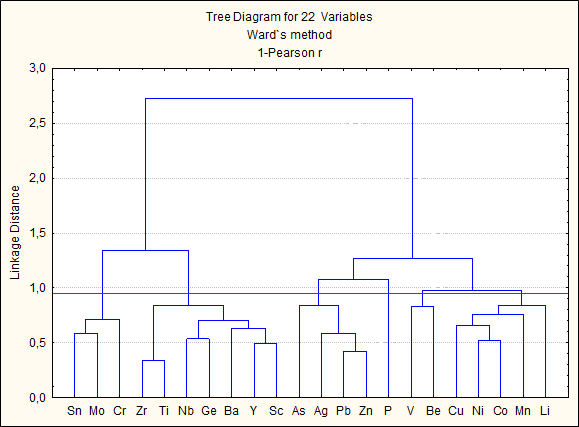 Рисунок 10 – Дендрограмма корреляционной матрицы геохимического спектра элементов в пробах участка Бургали (1-Pearson r (0,05) = 0,90; объем выборки – 1970 проб) 4.8 Факторный дисперсионный анализ Факторный анализ дает возможность сокращения числа переменных (редукция данных) и определения структуры взаимосвязей между переменными, т.е. классификации переменных. Сокращение проводится с помощью выделения скрытых общих факторов, разъясняющих связи между наблюдаемыми признаками объекта [10]. В основе факторного анализа лежит использование зависимости между переменными: производится ввод новой переменной на основе регрессии, то есть переменная включает в себя наиболее важные черты исходных переменных, следовательно, использование данной переменной (замена нескольких старых коррелированных переменных одной новой) ведет к сокращению числа переменных. Новый фактор (переменная) является линейной комбинацией исходных переменных. Принцип данного метода или анализ главных компонент состоит в представлении двух или более зависимых переменных одним фактором. После выделения первого фактора, то есть, построения первой линии регрессии, для которой дисперсия максимальна (в основе факторных нагрузок лежит дисперсия), определяется следующая линия, максимизирующая остаточную вариацию (разброс данных вокруг первой прямой), то есть выделяется второй фактор, и т.д. Факторы независимы друг от друга. Остановка процесса выделения факторов проводится в зависимости от того, что считать малой "случайной" изменчивостью. Рациональный выбор числа факторов проводится с использованием: критерия накопленной или кумулятивной дисперсии, критерия Кайзера, критерия каменистой осыпи. Часто используется несколько видов критериев, а затем выбирается наиболее «осмысленный вариант» и соответствующее ему число факторов [6]. Для предания факторам простой интерпретации пространство факторов подвергнуто вращению так, что факторы отмечены высокими нагрузками для одних переменных, низкими нагрузками для других, и когда сохраняется немного высоких поперечных нагрузок, то есть, немного переменных с существенными нагрузками на больше чем одном факторе. Самый стандартный вычислительный метод вращения, чтобы вызвать простую структуру – варимакс-вращение [7]. Таблица 8 – Значения вращаемых факторных нагрузок в выбранной 3-х факторной модели
Согласно таблице 8, высокие факторные нагрузки химических элементов распределились по факторам следующим образом: Значимых факторных нагрузок в программе выделено не было, возможно в связи с многими заменами ураганных значений, но мною были выделены высокие среди прочих значения. Фактор Ф1 – наиболее весомый, составной, характеризуется в основном ассоциацией элементов Sc-Ti-Sn, связанной с Ф1 отрицательной корреляционной связью. Фактор Ф2 – характеризуется отрицательной связью с Zr, а фактор Ф3 – положительной связью с Be. 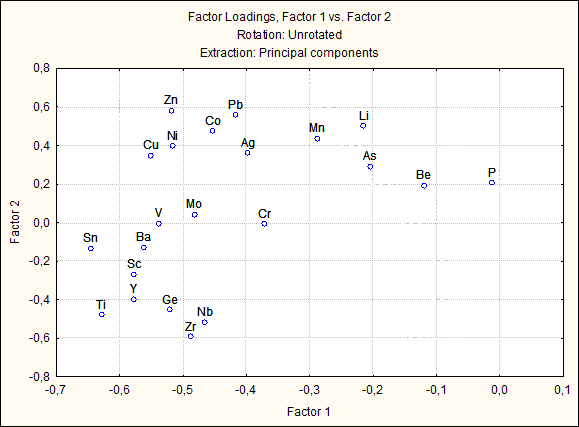 Рисунок 11 – Двумерный график факторных нагрузок элементов в выборке литегеохимических проб участка Бургали График, показанный на рисунке 11, иллюстрирует соотношение между факторами и группами переменных. Возможно выделить две крупных микроассоциации, Zn-Ni-Cu-Co-Pb-Ag, испытывающие среднее положительное влияние фактора 2 и среднее отрицательное влияние фактора 1, а также микроассоциацию Sn-Ba-V-Mo-Sc-Y-Ti-Ge-Zr-Nb, испытывающую только среднее отрицательное влияние фактора 1. 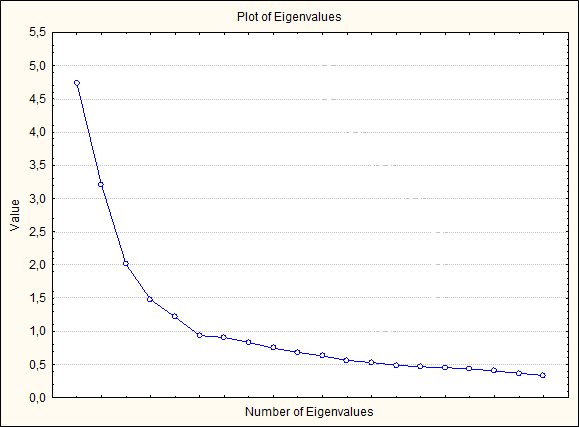 Рисунок 12 – График собственных значений («критерий каменной осыпи») Рисунок 12 демонстрирует графический метод («критерий каменистой осыпи») оценки значимости собственных значений: справа от критической точки, где убывание собственных значений слева направо максимально замедляется, находится только «факториальная осыпь», которой пренебрегают. Таким образом, выбирают необходимое для анализа количество факторов. В моем случае согласно рисунку 11 необходимо проанализировать 3 фактора. Факторы были проанализированы ранее в результате факторного анализа. Рисунок 13 подтверждает выводы, сделанные при анализе рисунка 10. 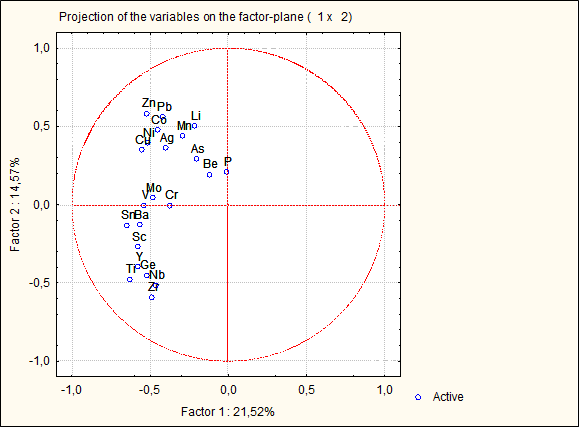 Рисунок 13 – Результаты факторного анализа в виде круговой диаграммы содержаний химических элементов в выборке проб участка Бургали ЗАКЛЮЧЕНИЕ В процессе выполнения работы проведен статистический анализ содержаний химических элементов в выборке проб участка Бургали. В работе отображена информация, полученная в результате литературного обзора, изучения методик геохимических работ, а также результаты статистического анализа геохимической информации. Получены основные выводы: 1.Анализ диаграмм размаха позволил подтвердить закон Оддо-Гаркинса и закон Кларка-Вернадского. 2.Результатом рассмотрение матриц корреляционных связей химических элементов в пробах было выделение разных по силе корреляционных связей – наиболее сильная положительная корреляционная связь отмечается для пары Sn-W (0,69), наибольшая отрицательная – для пары Zn-Ba (-0,42). 3. Благодаря кластерному анализу выявлены 3 крупных микроассоциаций {Zr-Ti-Nb-Ge-Ba-T-Sc, As-Ag-Pb-Zn, Cu-Ni-Co-Mn-Li}. 4. Факторный дисперсионный анализ выявил 3 основных фактора, связанных с природными источниками. 5. График, показанный на рисунке 10 и 12, иллюстрирует соотношение между факторами и группами переменных. Возможно выделить две крупных микроассоциации, Zn-Ni-Cu-Co-Pb-Ag, испытывающие среднее положительное влияние фактора 2 и среднее отрицательное влияние фактора 1, а также микроассоциацию Sn-Ba-V-Mo-Sc-Y-Ti-Ge-Zr-Nb, испытывающую только среднее отрицательное влияние фактора 1. Полученные практические навыки статистического анализа позволят в будущем более тщательно анализировать геохимическую информацию. БИБЛИОГРАФИЧЕСКИЙ СПИСОК Боровиков, В. П. Популярное введение в современный анализ данных в системе STATISTICA. Методология и технология современного анализа данных: учебное пособие / В.П. Боровиков. – Москва: Горячая линия-Телеком, 2013. – 288 с. Буреева Н.Н. Многомерный статистический анализ с использованием ППП “STATISTICA”. Учебно-методический материал по программе повышения квалификации «Применение программных средств в научных исследованиях и преподавании математики и механики». Нижний Новгород, 2007, 112 с. Геохимия. Методические указания по выполнению лабораторных работ / Санкт-Петербургский горный ин-т. Сост.: А.Г. Марченко, В.В. Смоленский.СПб, 2006. 56 с. Инструкция по геохимическим методам поисков рудных месторождений. – М.: Недра, 1983. – 191 с. Каталог визуализации данных [Электронный ресурс]. – Режим доступа: https://datavizcatalogue.com/RU/index.html Михальчук, А.А., Язиков Е.Г. Многомерный статистический анализ эколого-геохимических измерений. Часть I. Математические основы Учебное пособие. – Томск: Изд. ТПУ, 2014. – 103 с. Михальчук, А.А., Язиков Е.Г. Многомерный статистический анализ эколого-геохимических измерений. Часть II. Компьютерный практикум. Учебное пособие. – Томск: Изд. ТПУ, 2014. – 150 с. Отчет о результатах работ по объекту 640-50 «Поисковые работы на золото в пределах Бургалинской перспективной площади (Амурская область)» Ткачев, Ю. А. Статистическая обработка геохимических данных: Методы и проблемы / Ю.А. Ткачев, Я.Э. Юдович; АН СССР. Коми филиал. Институт геологии. – М. : Наука, 1975. – 234 с. Халафян, А.А. STATISTICA 6. Статистический анализ данных. 3-е изд. Учебник. – М.: ООО «Бином-Пресс», 2007. – 512 с. Шестаков, Ю. Г. Математические методы в геологии: учебное пособие / Ю.Г. Шестаков. – Красноярск: Изд-во Красноярского ун-та, 1988. – 208 с. ПРИЛОЖЕНИЕ 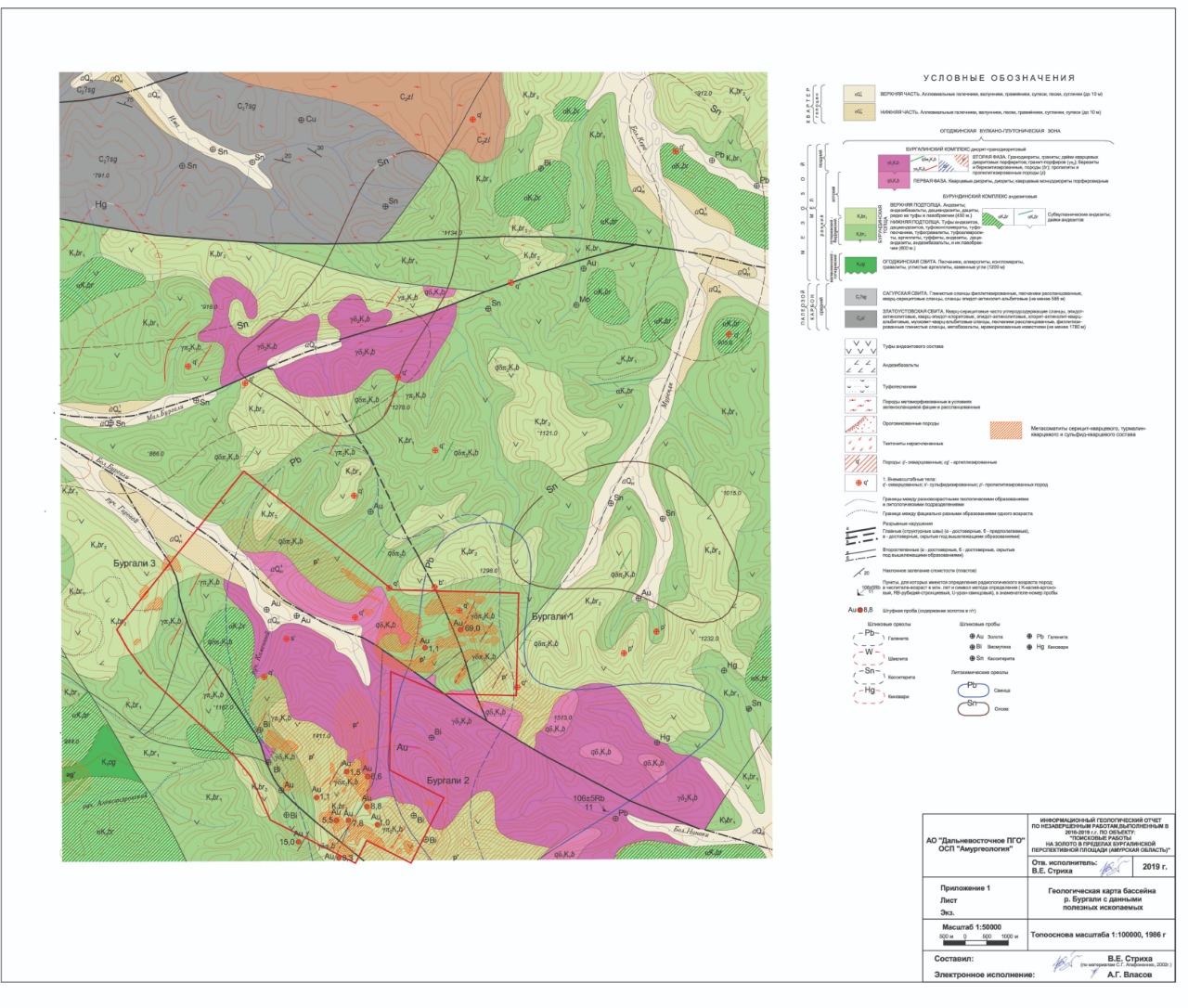 |
