математические методы. Мат методы практика. Отчет по лабораторным работам по дисциплине Математические модели и методы

• Название: Отчет по лабораторным работам по дисциплине Математические модели и методы
• Анкор: математические методы
• Дата: 31.01.2022
• Размер: 276.4 Kb.
• Имя файла: Мат методы практика.docx
• Тип: Отчет; #347407

Министерство науки и образования РОССИЙСКОЙ ФЕДЕРАЦИИ

федеральное государственное бюджетное

образовательное учреждение высшего образования

«Казанский государственный энергетический университет»
Кафедра «Инженерная кибернетика»


Отчет по лабораторным работам

по дисциплине «Математические модели и методы»

Выполнил:

Студент гр. ЗПИ-1-20

.
Проверил:

Казань 2022

Лабораторная работа №2.

Тема: Аппроксимация и интерполяция экспериментальных данных.

Краткая теория.

Различают два основных способа выбора приближения функций: интерполяцию и аппроксимацию. Аппроксимацией называется процедура построения функции, исходя из заранее определенного понятия близости.

Рассматривается выборка двух взаимосвязанных дискретных случайных величин X и Y. Пара x_i, y_i, где 1  i  n соответствует i-й точке (i-му опыту). Здесь n – объем парной выборки

Для удобства последующего использования табличные (опытные) данные моделируют некоторой функцией, которую называют уравнением регрессии:

Y  f X .

Процедура построения регрессионной (статистической) модели предусматривает, во-первых, выбор функции f (X.

В качестве функции чаще всего используют полином: ,

Y  a₀  a₁  X  a₂  X² … a_k  X^k, (4.1)

где a_j− коэффициенты регрессии 0  j k  ; k − порядок полинома.

На втором этапе построения модели определяют коэффициенты регрессии a_k. Это осуществляется путем аппроксимации опытных точек.

Уравнение регрессии позволяет вычислить ожидаемое значение функции Y для опытных значений x_i:

Y (x_i)  a₀  a₁  x_i  a₂  x_i² … a_k  x_i^k (4.2)

Разность между опытным значением y_i и ожидаемым значением Y x_i составляет ошибку или погрешность функции:

Y_i  y_i  Y( x_i ) (4.3)

Аппроксимация может быть произведена при разных требованиях к величине Y_i. Наиболее распространенным является требование минимизации суммы квадратов отклонений опытных точек от линии регрессии. Это требование называют принципом Лежандра, согласно которому коэффициенты регрессии a_j должны быть подобраны так, чтобы сумма: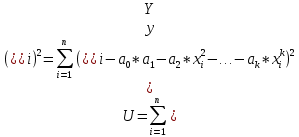

(4.4)

принимала минимальное значение.

Метод определения коэффициентов регрессии по принципу Лежандра называют методом наименьших квадратов.

Искомые коэффициенты регрессии находятся из решения системы уравнений: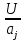

 0.

Для анализа общего качества уравнения регрессии используют обычно множественный коэффициент детерминации R², называемый также квадратом коэффициента множественной корреляции R. R² (мера определенности) всегда находится в пределах интервала [0; 1].

Если значение R² близко к единице, это означает, что построенная модель объясняет почти всю изменчивость соответствующих переменных. И наоборот, значение R-квадрата, близкое к нулю, означает плохое качество построенной модели.

Коэффициент детерминации R² показывает, на сколько процентов (R²*100 %) найденная функция регрессии описывает связь между исходными значениями факторов X и Y:


Вариант 2.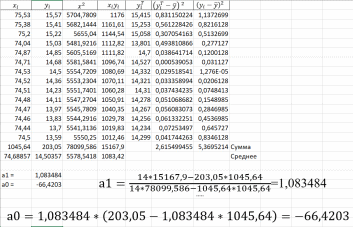



График и графическое представление отклонений: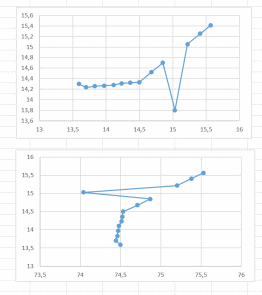



Коэффиценты линейной регрессии равны:

а₁= 1,083484

а₀=-66,4203

Таким образом, искомая регрессионная зависимость имеет вид:

y^T=1.083484+66,4203х

Коэффициент детерминации:

R²=0.487101

Результаты по регрессионной статистике: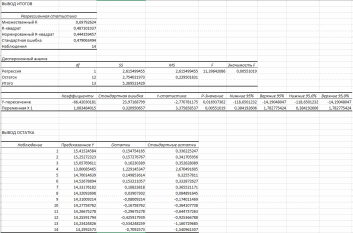



График тренда: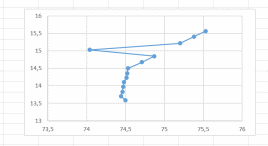



Вывод: Для проведения регрессионного анализа и прогнозирования построили график исходных данных и попытались зрительно, приближенно определить характер зависимости; выбрали вид функции регрессии, которая может описывать связь исходных данных; определили численные коэффициенты функции регрессии методом наименьших квадратов; оценили силу найденной регрессионной зависимости на основе коэффициента детерминации R²; сделали прогноз с помощью найденной регрессионной зависимости.
Интерполяция функции.

Результаты экспериментов обычно бывают представлены ограниченным числом в виде таблиц, отражающих зависимость величины исследуемого явления y от фактора x. При этом величины x_i, где 0  i  n, образуют n  1 узловую точку. Для практического применения, как правило, необходимо знать и промежуточные, по отношению к табличным, значения y.

Если интерполирующая функция g x строится на всем интервале изменения аргумента х₀, х_n , то такая интерполяция называется глобальной.

Если интерполяционные многочлены строятся отдельно для разных частей рассматриваемого интервала изменения x, то говорят о локальной интерполяции.

В тех случаях, когда интерполяционные многочлены используются для приближенного вычисления функции вне рассматриваемого отрезка  x  x₀, x  x_n, приближение функции называют экстраполяцией.

Интерполирующая функция g x принимает в узлах xi те же значения y_i, что и функция f x, т.е.

g(x_i)  y_i, i = 0, 1, …, n. (4.12)

Выражение для g  x выбирают так, чтобы оно позволяло достаточно легко вычислять значения интерполирующей функции. После этого полагают f x  g x для всех x из  х₀, х_n . Чаще всего g x представляют в виде полинома, максимальная степень которого при числе узлов n 1 составляет n:

g(x)  a₀  a₁  x  a₂  x²  ...  a_n  xⁿ. (4.13)

Примером глобальной интерполяции могут служить многочлены Ньютона и Бесселя, рассмотренные ниже для случая равноотстоящих значений аргумента, т.е. шаг h = x_i - x_i-1 = const (i = 1, 2, …, n).
Интерполяция полиномами Ньютона.

Первая интерполяционная формула Ньютона (или интерполяционный многочлен для интерполирования вперед) имеет вид:

(4,14)

Вторая интерполяционная формула Ньютона (или интерполяционный многочлен для интерполирования назад) записывается в виде:

(4,15)

1. Функция рассчитывается для значения аргумента T = 110, принадлежащего левой половине рассматриваемого отрезка [100, 180] по формуле (4.14).

2. Рассчитаем вспомогательные величины.

Максимальная степень интерполяционного полинома n должна быть на единицу меньше числа узловых точек. В нашем случае узловых точек k = 5, а степень полинома n = 4.

h = T1 – T0 = 120 – 100 = 20

При T = 110 имеем .

3. Результаты расчетов конечных разностей функции y (в нашем случае это давление насыщенного пара P) представим в табличном виде:



4. Исходная формула в нашем случае (n = 4) будет иметь вид:



Используя ее, выполним расчеты: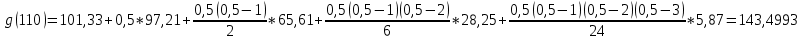


Интерполяционная формула Лагранжа.

Формула интерполяционного многочлена Лагранжа:

(4,16)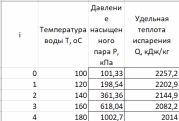



P=110C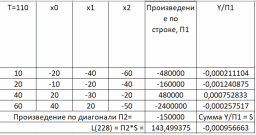



Вывод: Значения совпадают по интерполяции полиномами Ньютона – 143,4993. По интерполяционной формуле Лагранжа – 143,499375.