Тема 1. Отчет по лабораторным занятиям по дисциплине Экономика инжиниринга
 Скачать 221.22 Kb. Скачать 221.22 Kb.
|
|
ПЕРВОЕ ВЫСШЕЕ ТЕХНИЧЕСКОЕ УЧЕБНОЕ ЗАВЕДЕНИЕ РОССИИ  МИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ федеральное государственное бюджетное образовательное учреждение высшего образования санкт-петербургский горный УНИВЕРСИТЕТ Кафедра экономики, организации и управления Отчет по лабораторным занятиям по дисциплине «Экономика инжиниринга» (наименование учебной дисциплины согласно учебному плану) Тема: «Основы экономики инжиниринга» Автор: студент гр. _________________ __/Самариной Е. С./ (подпись) (Ф.И.О.) ОЦЕНКА: _________ Дата: _________ ПРОВЕРИЛ: доцент _________________ / Любек Ю. В./ (подпись) (Ф.И.О.) Санкт-Петербург 2021 Задание 1. Компания 7 лет назад приобрела воздушный компрессор за 2500 руб. Годовой доход от сдачи в аренду компрессора составил 750 руб. 100 рублей было потрачено на техническое обслуживание в первый год, и ежегодно эта сумма увеличивалась на 25 руб. Компания планирует продать компрессор в конце следующего года за150. Необходимо построить диаграмму денежных потоков с точки зрения компании и укажите, текущее положение. Пусть текущее время это t=0. Доходы и расходы приведены в таблице с чистым денежным потоком. Чистые денежные потоки (один отрицательный, восемь положительных) показаны на рисунке. Текущая стоимость P находится в году 0. Решение: Для того, чтобы найти чистые денежные потоки за 9 периодов, нужно посчитать CIF (притоки) и COF (оттоки). Расчеты представлены на рисунках 1 и 2.  Рисунок 1. Расчет показателей притоков и оттоков  Рисунок 2. Расчеты в режиме отображения формул Таким образом, получили 1 поток отрицательный и 8 положительных. 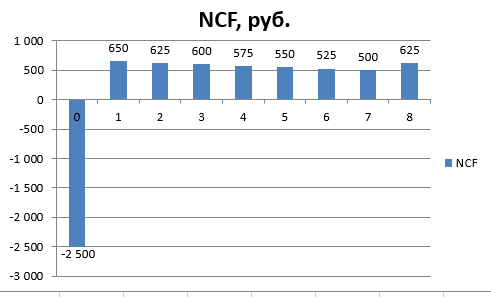 Рисунок 3. График чистых денежных потоков Задание 2. 1 мая сотрудник компании заимствует 100 000 рублей и должен выплатить в общей сложности 107 000 ровно через год. Необходимо определить сумму процентов и процентную ставку. Решение: 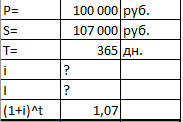 Рисунок 4. Исходные данные для решения задачи 2 На рисунке 4 представлены исходные данные. Чтобы найти процентную ставку и сумму процентов необходимо использовать формулу сложной учетной ставки. Таким образом, находим (1+i)^t, которое равно 1,07. 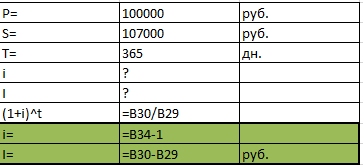 Рисунок 5. Расчет процентной ставки и суммы процентов Рисунок 6. Результаты решения задачи Таким образом, получаем, что процентная ставка по данному займу составила 7%, а общая сумма процентов с займа равна 7 000 рублей. Задание 3. Необходимо рассчитать сумму, внесенную 1 год назад и начисленные проценты, чтобы сегодня в общей сложности на руки получить 100000 рублей с процентной ставкой 5% годовых. Решение: Используем сложную ссудную ставку.  Рисунок 7. Расчет первоначальной суммы Р и начисленных процентов I Рисунок 8. Результаты решения задачи 3 Таким образом, нашли первоначальную сумму, равную 95 238,1 рублей и сумму начисленных процентов, равную 4 761,9 рублей. Также удалось рассчитать результат, используя функцию ПС (первоначальная стоимость). Рисунок 9. Расчет в режиме отображения формул Результат получился такой же, как и при ручном расчете, значит результат верный. Задание 4. Финансовая корпорация предоставила машиностроительной компании 10 000 000 руб. на модернизацию системы по защите окружающей среды. Ссуда выдана на 3 года под 10% с простым начислением. Какую сумму необходимо возместить через три года? Решение: В данной задаче используем простую ставку ссудных процентов.  Рисунок 9. Расчет суммы возврата Рисунок 10. Результаты расчета Таким образом, через три года компания должна будет вернуть при предоставленных условиях 14 285 714 рублей. Задание 5. В таблице ниже представлены четыре различных плана погашения кредита. Каждый план предусматривает погашение кредита в размере 5000 рублей за5 лет при 8% в год. План 1: оплатить все по окончании. Никакие проценты или основная сумма не выплачиваются до конца пятого года. Проценты ежегодно накапливаются по основной сумме и по всем начисленным процентам. План 2: ежегодная выплата процентов, погашение основного долга через 5 лет. Начисленные проценты выплачиваются каждый год, а весь основной капитал выплачивается в конце пятого года. План 3: выплачивать проценты и часть основной суммы ежегодно. Начисленные проценты и одна пятая часть основной суммы (или 1000 рублей) погашаются каждый год. Непогашенный остаток по ссудам уменьшается каждый год, поэтому процент на каждый год уменьшается. План 4: Оплатить равными частями проценты и основную сумму. Равные выплаты производятся каждый год, причем часть идет на погашение основного долга, а остаток покрывает начисленные проценты. Поскольку остаток по кредиту уменьшается со скоростью, меньшей, чем в плане 3, из-за равных платежей в конце года, процент уменьшается, но медленнее. Необходимо сделать выводы об эквивалентности каждого плана с 8%-ным сложным процентом. Разработать простой процентный план погашения задолженности по кредиту на 8% в год, используя тот же подход, что и в плане 2. Решение:  Рисунок 11. Расчет накопленной суммы долга по плану 1 В первом плане заемщик выплачивает проценты и тело кредита в конце срока кредитования. Используем для расчета сложную учетную ставку и рассчитываем, накапливая общую сумму и начисляя процент на сумму на конец предыдущего года.  Рисунок 12. Расчет в режиме отображения формул Рисунок 13. Результат расчетов по первому плану Таким образом, получаем что общая переплата составит 2 346,64 рубля. Рассчитаем сумму процентов в соответствии со вторым планом. В данном плане выплачивают проценты каждый год, а тело кредита в конце срока кредитования.  Рисунок 14. Расчет накопленной суммы долга по плану 2  Рисунок 15. Расчет в режиме отображения формул Рисунок 16. Результат расчетов по второму плану Таким образом, накопленная сумма процентов составит 2 000 рублей. В рамках третьего плана выплачивается одна пятая сумма основного долга и начисленные проценты каждый год. 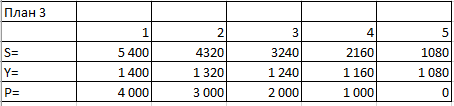 Рисунок 17. Расчет накопленной суммы долга по плану 3  Рисунок 18. Расчет в режиме отображения формул Рисунок 19. Результат расчетов по третьему плану Таким образом, по третьему плану результаты следующие: общая сумма процентов составит 1 200 рублей. В четвертом плане долг выплачивается равными частями. В этом случае используем расчет плана погашения долга равными срочными уплатами Y. 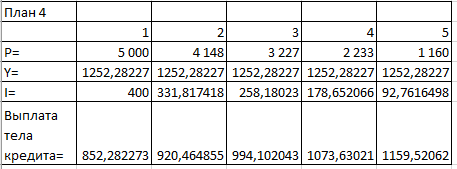 Рисунок 20. Расчет накопленной суммы долга по плану 4  Рисунок 21. Расчет в режиме отображения формул Рисунок 22. Результат расчетов по четвертому плану Таким образом, по четвертому плану сумму процентов получили равную 1 261 рублю. В общем результате можно сказать, что наиболее эффективный план выплаты кредита является третий план, так как переплата в сравнении с другими планами будет наименьшей. Рассчитаем план выплаты кредита с простой учетной ставкой по модели второго плана. 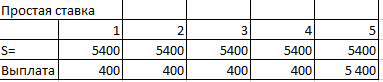 Рисунок 23. Расчет накопленной суммы долга по плану 2 с простой ставкой  Рисунок 24. Расчет в режиме отображения формул Рисунок 25. Результат расчетов по второму плану с простой ставкой Таким образом, используя простую учетную ставку по второму плану, получили такой же результат, так как процент и в том и в другом случае начисляется на тело кредита и выплачивается в конце каждого года. Задание 6. Найти A, используя функцию электронных таблиц =А (5%,5,5500). Решение: В данной задаче необходимо рассчитать первоначальную сумму, которая за 5 лет при 5% годовых вырастет до 5 500 рублей. Рисунок 26. Расчет в режиме отображения формул Таким образом, получили, что нужно положить 1 270 рублей, чтобы через 5 лет получить 5 500 рублей. Задание 7. P=100 000, F=?, i=8%, n=20 лет. Решение: Рассчитываем, будущую стоимость 100 000 рублей через 20 лет при 8% годовых. Рисунок 27. Расчет в режиме отображения формул Таким образом, будущая стоимость равна 466 095 рублей. Задание 8. A =600, i = 16%, n = 9 лет, P- ? Решение: Рассчитаем, сколько будут стоить накопленные деньги сегодня. Рисунок 28. Расчет в режиме отображения формул Получили сумму, равную 2 763 рублей. |
