Статистический анализ данных. Лаб5. Отчет по лабораторной работе 5 Статистический анализ производственных данных
 Скачать 97.02 Kb.
|
|
Факультет: Автоматизированные информационные технологии Кафедра: Информационные технологии и системы Дисциплина: «Методологии и технологии проектирования информационных систем» ОТЧЕТ ПО ЛАБОРАТОРНОЙ РАБОТЕ №5 «Статистический анализ производственных данных» Вариант 49 Выполнил: студент группы 21ИС1м Черяпкин А.Д. Проверил: к.т.н., доцент Жашкова Т.В. Работа зачтена с оценкой: ______________ Пенза 2023 Цель работы – освоение методики подготовки и статистической обработки производственных данных, необходимых для последующего моделирования бизнес-процесса. Задача состоит в генерации случайных чисел, которые будут представлять производственные данные для выбранной предметной области. Дано: параметры для генерирования случайных чисел для моделирования бизнес-процессов (таблицы 5.1 – 5.2). Требуется: с помощью процедур генерирования случайных чисел программы MS Excel подготовить числовые данные, распределенные по заданным законам (п. 5.3); выполнить статистическую обработку результатов моделирования: вычислить оценки параметров распределения и проверить соответствие экспериментальных данных заданной функции распределения с использованием критерия Пирсона (п. 5.4). Таблица 5.1 – Данные для генерации чисел при нормальном законе распределения
Таблица 5.2 – Данные для генерации чисел с равномерным распределением
Генерация данных о продолжительности работы Для выполнения пункта 1 задания следует обратиться к процедуре генерации случайных чисел с помощью команд меню MS Excel: «Данные» / «Анализ данных» / «Генерация случайных чисел» (рисунок 5.1). После вывода формы (рисунок 5.2) следует ввести значения параметров из таблицы 5.1, при этом задать число переменных, равное 1, и нормальное (или равномерное) распределение чисел. В качестве выходного интервала можно использовать любой столбец таблицы MS Excel, например, столбец «А», как показано на рисунке 5.3. 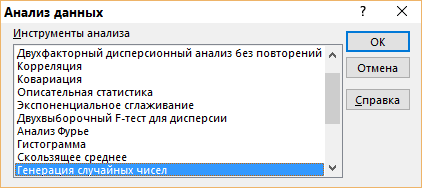 Рисунок 5.1 – Меню для выбора функции анализа данных 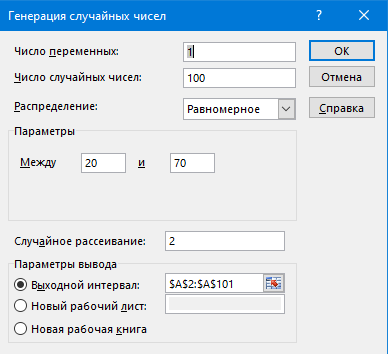 Рисунок 5.2 – Форма для назначения параметров генерации случайных чисел 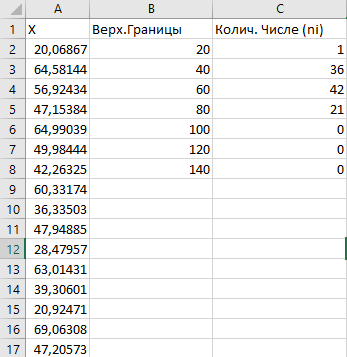 Рисунок 5.3 – Пример размещения чисел в MS Excel Статистическая обработка результатов Выполнить статистическую обработку данных по следующему алгоритму: вычислить наименьшее и наибольшее значения полученных чисел (Хмин, Хмакс) с помощью функций A104=МИН(А2:А101); A105=МАКС(А2:A101);  разделить диапазон (Хмин, Хмакс) на k равномерных интервалов и записать верхние границы интервалов в ячейки (например, в колонку B) MS Excel (рисунок 5.3): B2=A104; B3=B2+А104 и т.д.; при 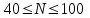 значение k рекомендуется выбрать из интервала ;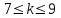выделить массив (например, C2:C8, рисунок 5.3) для формирования данных о частоте попадания отказов в каждый из заданных интервалов (количество ячеек на одну больше, чем количество интервалов; задать для него использование функции ЧАСТОТА(массив_данных; массив_интервалов); «Массив_данных» — обязательный аргумент, - массив или ссылка на множество значений, для которых вычисляются частоты, например, A2:A31 (рисунок 5.3); «Массив_интервалов» — обязательный аргумент, - массив или ссылка на множество интервалов, в которые группируются значения аргумента «массив_данных», например, C2:C8 (рисунок 5.3). Для применения функции «ЧАСТОТА» к массиву ячеек надо выделить ячейки, например, C2:C8; в поле ввода формул ввести функцию «ЧАСТОТА», задать для неё аргументы, например, ЧАСТОТА(A2:A101; В2:В8) и нажать клавиши CTRL+SHIFT+ENTER; число в ячейке C8 будет содержать количество чисел, превышающих установленную верхнюю границу, например, после Хмакс (рисунок 5.3); вычислить выборочное среднее: 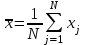 ;можно использовать функцию MS Excel: СРЗНАЧ(A2:A101); вычислить выборочное среднеквадратическое отклонение для нормального распределения: 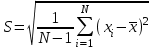 ;можно использовать функцию MS Excel: СТАНДОТКЛОН.В(A2:A101); вычислить значения теоретических частот 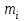 , i=1, 2, …, k, используя функции MS Excel (рисунок 5.4); при 100 значениях случайных чисел значения теоретических частот для нормального распределения вычисляются таким образом: 100*(НОРМ.РАСП(B2;$D$2;$E$2;ИСТИНА) – НОРМ.РАСП(0;$D$2;$E$2; ИСТИНА)); при этом первый аргумент в уменьшаемом принимает значения B2, В3, …, В7, а вычитаемом – 0, B2, В3, …, В6; для равномерного распределения значения теоретических частот одинаковы для всех k интервалов: 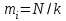 .Значения выборочных частот выбираются (в данном примере) из ячеек С2, С3, …, С8. 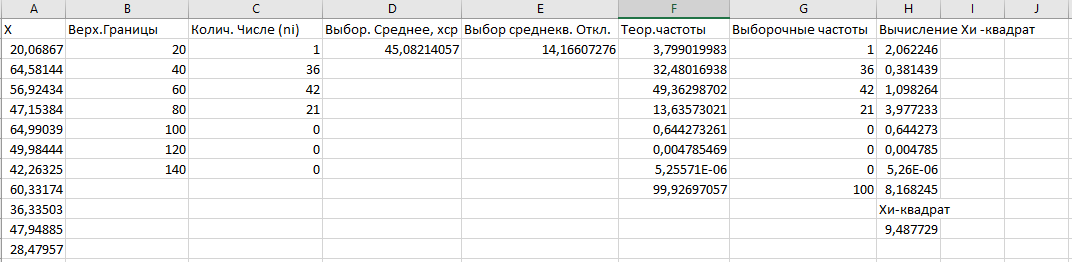 Рисунок 5.4 – Пример размещения результатов вычислений по полученным значениям построить графики частот (рисунок 5.5); для подписей оси абсцисс использовать ячейки В2:В8; 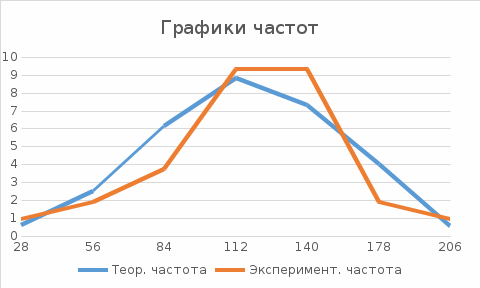 Рисунок 5.5 – Графики частот вычислить значение критерия по экспериментальным данным: 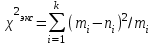 ;вначале вычислить отношение квадрата разности теоретических и экспериментальных частот к соответствующим значениям теоретических частот 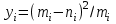 ;по данным примера (рисунок 5.4) в MS Excel используется выражение: (F2-G2)*(F2-G2)/F2; результаты размещены в столбце Н для всех интервалов, рисунок 5.4; затем - сумму чисел в столбце Н: СУММ(H2:H8); вычислить табличное значение критерия 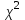 при известных значениях уровня значимости 0,05 и числе степеней свободы S=k-p-1 в MS Excel с помощью функции =ХИ2.ОБР.ПХ(0,05;4), где k – количество интервалов; p – количество параметров функции распределения (значение 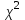размещено в ячейке Н12, рисунок 5.4); значение p равно 2 для нормального распределения и равно 1 для равномерного распределения;если выполняется условие: 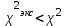 , то можно принять гипотезу о соответствии эмпирических данных выбранному теоретическому закону распределения (по заданию: нормальному или равномерному). В зависимости от версии MS Excel для вычисления табличного значение критерия 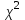могут использоваться разные варианты функций (рисунок 5.6).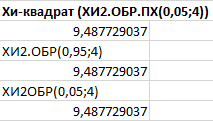 Рисунок 5.6 – Использование вариантов функций в MS Excel для вычисления значения 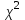| ||||||||||||||||||||||||||||