Лабораторные работы. Отчет по лабораторной работе по физике студент Группа
 Скачать 0.67 Mb.
|
ВЫЧИСЛЕНИЯПроводились в программе Excel.ВЫВОДЫНа основе проведенных измерений построены графики зависимостей Вэксп= f(х) и Втеор = f(х). Видно, что характер зависимостей примерно одинаков, между ними имеется корреляция. Расхождение между Вэксп и Втеор можно объяснить погрешностями измерений.КОНТРОЛЬНЫЕ ВОПРОСЫ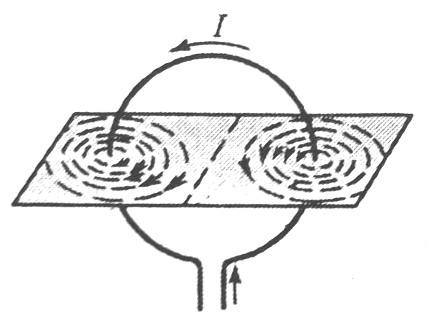 1. Изобразить магнитное поле кругового тока. Является ли оно однородным?Магнитное поле кругового тока неоднородно. Однородным называют магнитное поле, линии индукции которого параллельны друг другу, а величина магнитной индукции одинакова во всех точках. 2. В формулу (3) входит векторное произведение [  ]. Объяснить, как определяются модуль и направление вектора, получающегося в результате векторного перемножения двух векторов.Модуль вектора  определяется по формуле  где  ‒ угол между векторами  и  . Направление определяется правилом векторного произведения или «правилом буравчика» (правилом «правого винта»): буравчик нужно расположить перпендикулярно плоскости, в которой размещены векторы и , и повернуть его в направлении от первого вектора ко второму; при этом буравчик будет двигаться поступательно в направлении, перпендикулярном указанной плоскости. Направление поступательного движения буравчика будет совпадать с направлением вектора .КОНТРОЛЬНЫЕ ЗАДАНИЯ
1. Замкнутый проводящий контур с током произвольной геометрической формы, помещенный в магнитное поле, испытывает действие вращающего момента сил  =  .Вращающий момент сил направлен перпендикулярно к плоскости, образованной векторами  и  , в соответствии с правилом векторного произведения. Вращающий момент стремится привести контур в положение устойчивого равновесия, при котором вектор совпадает по направлению с вектором .Модуль момента силы рассчитывается по формуле: М =  ,где – угол между векторами и .На рисунке вектор направлен к наблюдателю.2. По принципу суперпозиции магнитная индукция результирующего поля равна векторной сумме магнитных индукций полей отдельных источников:  .Направления векторов  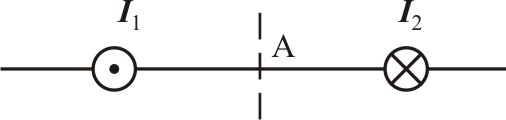и  определяются по правилу буравчика. Вектор магнитной индукции поля, созданного обоими проводниками с током, сонаправлен с векторами и . Если точка А равноудалена от проводников, то векторы магнитной индукции при равенстве сил тока в них равны по модулю.   3. Так как величина магнитной индукции прямо пропорциональна силе тока в проводнике и обратно пропорциональна расстоянию до проводника  , то при условии I1=2I2 искомая точка, в которой В = 0, должна лежать на расстоянии в 2 раза большем от первого проводника, чем от второго:  .В этом случае  , а результирующая магнитная индукция В = 0.Между проводниками 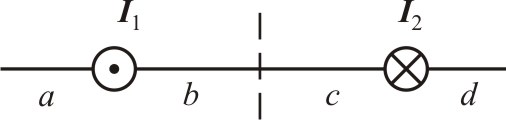 (см. задание 2). Значит, искомая точка, в которой В = 0, лежит правее проводника с током I2, т.е. на участке d. 4. По принципу суперпозиции магнитная индукция результирующего поля равна векторной сумме магнитных индукций полей отдельных источников:  .  Так как по модулю векторы магнитной индукции равны, то при сложении четырёх векторов, изображенных на рисунке, результирующий вектор будет равен нулю. Поэтому в точке А пересечения диагоналей квадрата индукция магнитного поля В = 0. ЛАБОРАТОРНАЯ РАБОТА № 60. ИЗУЧЕНИЕ СПЕКТРА АТОМА ВОДОРОДА. Цель работы: изучить теорию атома Томсона, Резерфорда и Бора, определить постоянную Ридберга. Теоретическое введение. Первая попытка создания на основе накопленных экспериментальных данных модели атома принадлежит Томсону (1903 г.). Согласно этой модели, атом представляет собой непрерывно заряженный положительным зарядом шар радиусом порядка 10-10 м, внутри которого около своих положений равновесия колеблются электроны. Суммарный отрицательный заряд электронов равен положительному заряду шара, поэтому атом в целом нейтрален. Через несколько лет Резерфордом было доказано, что представление о непрерывно распределенном внутри атома положительном заряде ошибочно. Опытами Резерфорда по рассеянию -частиц в 1911г. было установлено, что атом любого химического элемента состоит из положительно заряженного ядра и вращающихся вокруг него электронов. Масса атома почти полностью сосредоточена в его ядре, однако, размеры ядра ничтожно малы по сравнению с радиусом атома, который, в свою очередь, может быть оценен как среднее расстояние от ядра до электронов. Классическая электродинамика не в состоянии объяснить стационарное состояние атома, потому что электроны, испытывая непрерывные ускорения, должны излучать в пространство электромагнитные волны и, следовательно, терять энергию. При этом излучаемый атомом спектр должен быть непрерывным. В результате потери энергии электрон должен упасть на ядро, а атом прекратить свое существование. Однако этого не происходит, и атом может находиться в стационарном состоянии неограниченно долго. Кроме этого, экспериментальные исследования показали линейчатость спектров излучения атомов (у газов и паров металлов). Для устранения данных противоречий в 1913 г. датский физик Нильс Бор выдвинул постулат (первый постулат Бора) согласно которому атом может находиться в стационарном состоянии неограниченно долго. Стационарным состояниям атома соответствуют стационарные орбиты, по которым движутся электроны. Атомы, находящиеся в стационарном состоянии, не излучают электромагнитных волн. Изучая энергетический спектр атома водорода, Бор пришел к выводу, что собственный момент импульса атома водорода Ln, который почти полностью совпадает с моментом импульса электрона относительно ядра, кратен  где, h=6,6210-34 Джс – постоянная Планка. , (1)где n=1, 2, 3, - целое положительное число, называемое главным квантовым числом; m - масса электрона, v - его скорость, а r - радиус орбиты. Соотношение (1) называется правилом квантования круговых орбит. Внутренняя энергия атома водорода складывается из кинетической энергии электрона относительно ядра (протона)  (2)и потенциальной, равной энергии кулоновского взаимодействия электрона и протона  , (3)где е =1,60210-19 Кл – модуль элементарного заряда; 0 =8,8510-12 Ф/м – электрическая постоянная. и потенциальной, равной энергии кулоновского взаимодействия электрона и протона Роль центростремительной силы, удерживающей электрон на стационарной орбите радиуса r, выполняет сила кулоновского притяжения между электроном и ядром:  . (4)Из сопоставления (2) и (4) видно, что  . (5)А полная энергия  . (6)Возведем соотношение (1) в квадрат, а соотношение (4) умножим на mr3 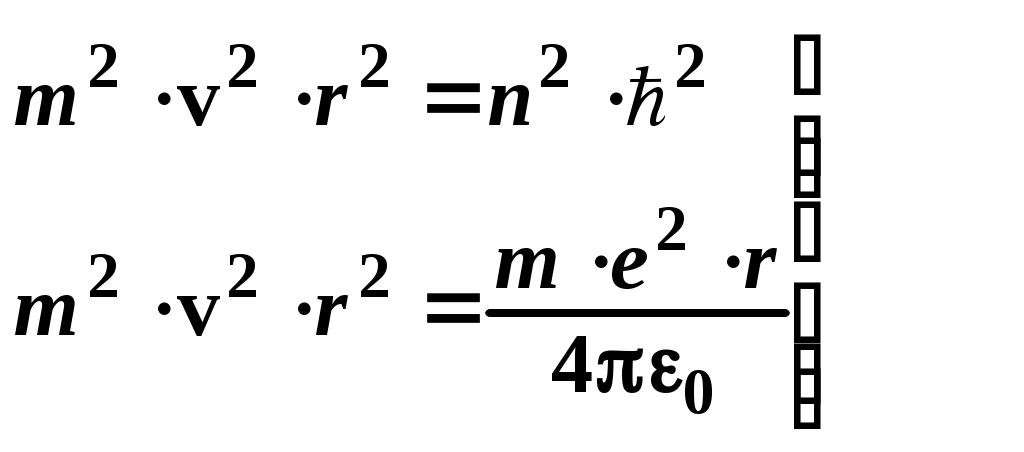 . (7)Левые части системы (7) одинаковы, а значит, правые равны друг другу:  , (8)откуда находятся радиусы стационарных орбит электрона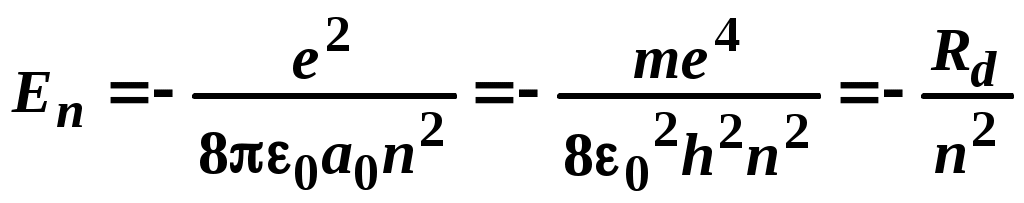:   , (9)где  = 0,52910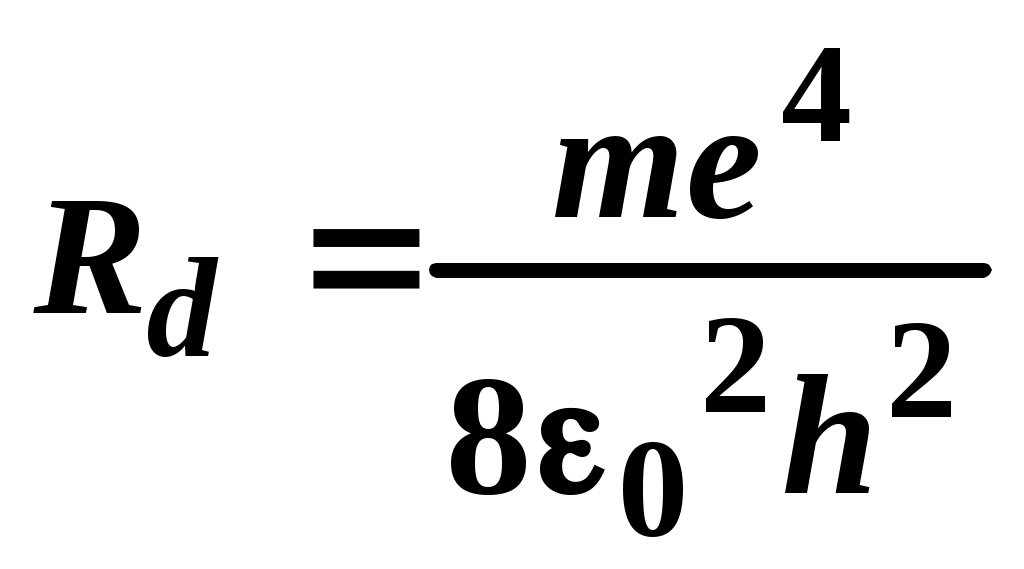-10 м = 0,529 Å (Å - ангстрем) – радиус первой орбиты электрона в атоме водорода. Подставляя (9) в (6), получим выражение для стационарных уровней энергии:  , (10)где  =2,1710-15 Дж=13,6 эВ – ридберг – атомная единица измерения энергии.Из соотношений (9) и (10) видно, что радиусы электронных орбит в атоме водорода и энергии электрона на этих орбитах полностью определяются главным квантовым числом n. Причем, радиус орбиты r пропорционален n2, а уровни энергии находятся в интервале от –13,6 эВ до нуля. На схеме (рис. 1) в соответствующем масштабе отложены уровни энергий с n=1,2,3. Видно, что энергия электрона возрастает с увеличением номера орбиты. Энергетическое состояние с n=1 является основным (нормальным) состоянием; состояния с n>1 являются возбужденными. Энергетический уровень, соответствующий основному состоянию атома, называется основным (нормальным) уровнем; все остальные уровни являются возбужденными. Согласно второму постулату Бора, при переходе электрона с более удаленной от ядра (высокой) k-ой орбиты на более близкую к нему (низкую) n-ую орбиту происходит испускание кванта излучения:  , (11)где Ek и En – соответственно энергии стационарных состояний атома до излучения и после излучения. 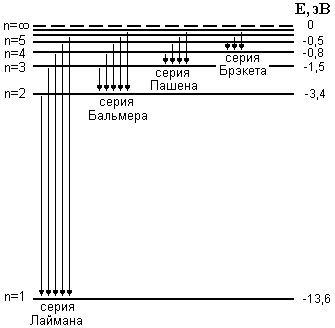 Рис. 1. Схема переходов, соответствующих спектру испускания атомов водорода. Наоборот, для того, чтобы перейти с низкой n-ой орбиты (более близкой к ядру) на более высокую k-ую орбиту, электрону необходимо поглотить такой же квант энергии h. Если каким-либо образом возбуждать атомы разряженного газа (с помощью электрического разряда, воздействием жесткого внешнего излучения, бомбардировкой пучком ускоренных частиц), то с помощью спектрального прибора можно наблюдать спектр излучения – узкие цветные линии на темном фоне. Цвет линии определяется частотой испускаемого света. Наоборот, если луч белого света пропускать через разряженный газ, то будет наблюдаться спектр поглощения – узкие темные полосы на сплошном спектре, причем поглощаются те же длины волн, что и излучаются. Возникновение спектра поглощения объясняется тем, что атомы газа способны поглощать только кванты света вполне определенной частоты. Подставим выражение для энергии (10) в формулу (11). Тогда частота фотона, излученного атомом водорода при переходе электрона с k-ой орбиты на n-ую (k>n), может быть найдена по формуле: 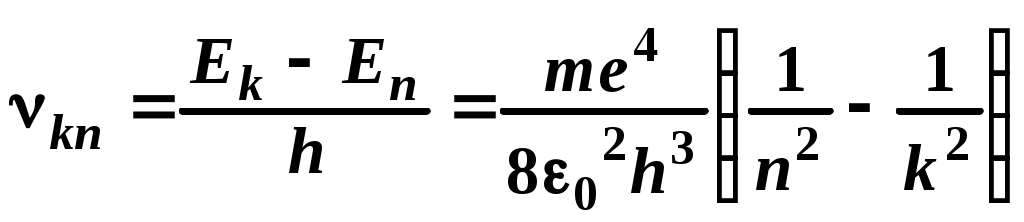 , (12)а соответствующая ей длина волны из соотношения: 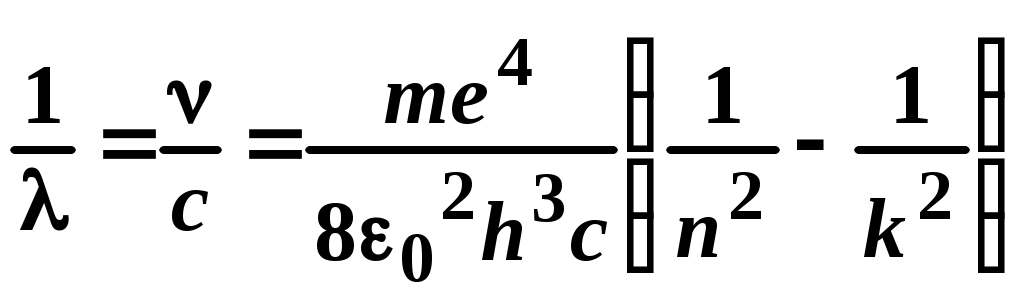 или  , (13)где 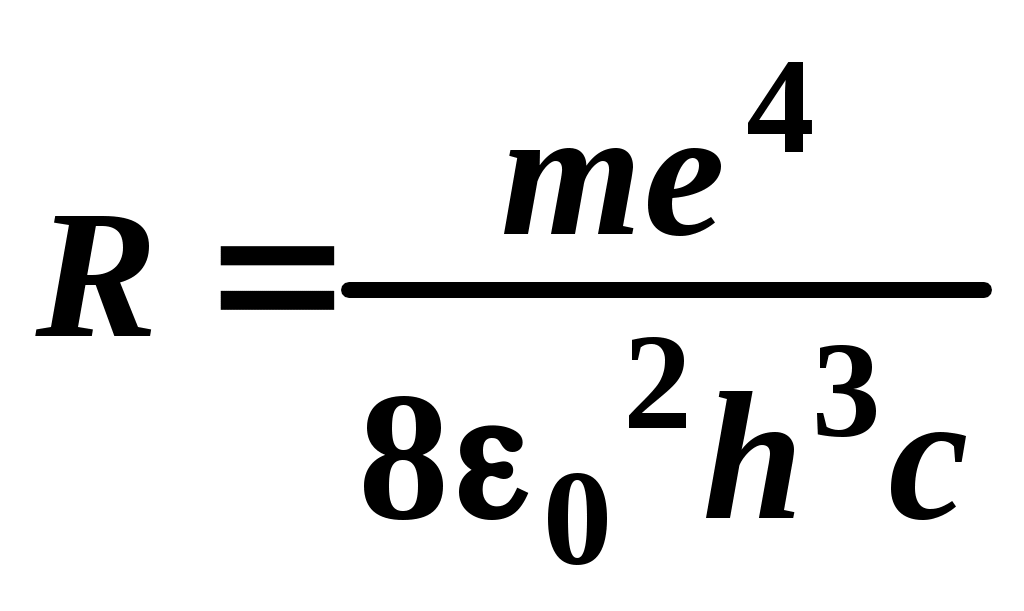 - постоянная Ридберга. (14)Соотношение (13) носит название формулы Бальмера, полученной эмпирически в 1885 г. Энергии квантов излучения и соответствующие им частоты объединяются в серии по номеру уровня, на который происходит переход электрона. |
Гн/м. Чему равна суммарная индукция магнитного поля в точке А?