Отчет Нартикоев. Отчет по практике Вид практики Производственная (преддипломная) практика Выполнил студент
 Скачать 0.88 Mb. Скачать 0.88 Mb.
|
3 Методы быстрого решения на основе предварительно подготовленных итерационных решателейВ этом разделе мы способствуем установлению эффективных методов решения группы линейных систем с матрицами коэффициентов Теплица, которые возникают из матричной формы неявной разностной схемы (2.1). Прежде всего выведем существенную матричную форму неявной разностной схемы (2.1). Используя обозначения из раздела 2, матрицу коэффициентов (2.1), соответствующую каждому временному уровню j, можно записать в следующем виде: 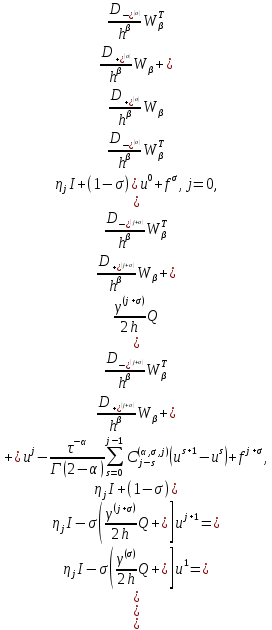 где у нас есть коэффициент 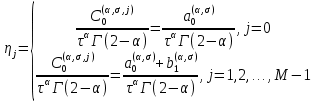 то 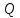 и и 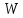 - две - две 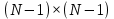 вещественные матрицы следующего вида вещественные матрицы следующего вида Очевидно, что 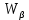 - Теплицева матрица (см. [14, 51, 58]). Следовательно, он может храниться с N + 1 записями [51]. - Теплицева матрица (см. [14, 51, 58]). Следовательно, он может храниться с N + 1 записями [51].3.1 Возникающие проблемы из дискретизированной схемыСогласно (3.1) и (3.2), это означает, что неявная разностная схема (2.1) требует решения несимметричной теплицевой линейной системы на каждом временном уровне j, точнее, существует последовательность несимметричных Теплицевых линейных систем 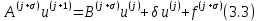 где 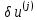 используется для обозначения вычисления используется для обозначения вычисления 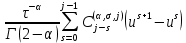 и 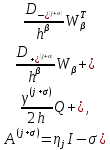 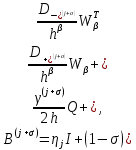 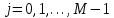 и и 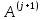 варьируется в зависимости от варьируется в зависимости от 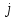 ; ; 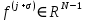 также меняется с также меняется с 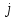 . Здесь следует подчеркнуть, что последовательность линейных систем (3.3) соответствует схеме с временным шагом (2.1), которая по своей сути является последовательной, поэтому последовательность линейных систем (3.3) чрезвычайно трудно распараллелить во времени. . Здесь следует подчеркнуть, что последовательность линейных систем (3.3) соответствует схеме с временным шагом (2.1), которая по своей сути является последовательной, поэтому последовательность линейных систем (3.3) чрезвычайно трудно распараллелить во времени.С другой стороны, замечательно, что если коэффициенты 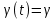 и и 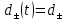 , то матрицы коэффициентов0 , то матрицы коэффициентов0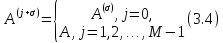 Кроме того, подчеркивается, что коэффициент 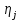 является действительной константой, которая не меняется при является действительной константой, которая не меняется при  . Другими словами, . Другими словами,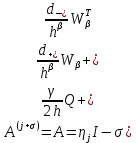 не зависит от 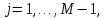 т.е. матрица коэффициентов (3.3) не меняется в каждом временном уровне т.е. матрица коэффициентов (3.3) не меняется в каждом временном уровне 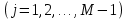 неявной разностной схемы. В этом случае, если мы по-прежнему решаем линейные системы (3.3) одну за другой, это не должно иметь смысла. Естественная идея для этого случая, чтобы найти обратную матрицу A Теплица, т.е. неявной разностной схемы. В этом случае, если мы по-прежнему решаем линейные системы (3.3) одну за другой, это не должно иметь смысла. Естественная идея для этого случая, чтобы найти обратную матрицу A Теплица, т.е. 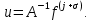 Это означает, что мы заинтересованы в вычислении Это означает, что мы заинтересованы в вычислении 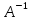 . Один из вариантов - вычислить обратную матрицу с помощью некоторых прямых методов, таких как LU-разложение [60, стр. 44-54]. Однако матрица Теплица часто бывает плотной, и вычисление обратной большой плотной матрицы является недопустимым, особенно когда матрица большая. К счастью, поскольку A также является матрицей Теплица, у нас есть формула Гохберга-Семенкула[51, 54] для ее обратной. Действительно, обратная к теплицевой матрице A может быть восстановлена по ее первому и последнему столбцам. Точнее, обозначим через . Один из вариантов - вычислить обратную матрицу с помощью некоторых прямых методов, таких как LU-разложение [60, стр. 44-54]. Однако матрица Теплица часто бывает плотной, и вычисление обратной большой плотной матрицы является недопустимым, особенно когда матрица большая. К счастью, поскольку A также является матрицей Теплица, у нас есть формула Гохберга-Семенкула[51, 54] для ее обратной. Действительно, обратная к теплицевой матрице A может быть восстановлена по ее первому и последнему столбцам. Точнее, обозначим через 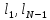 первый и последний столбцы первый и последний столбцы 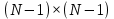 единичной матрицы, и пусть единичной матрицы, и пусть 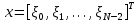 и и 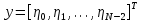 решения следующих двух теплицевых систем решения следующих двух теплицевых систем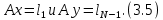 Если 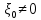 , то формулу Гохберга-Семенкула можно записать как , то формулу Гохберга-Семенкула можно записать как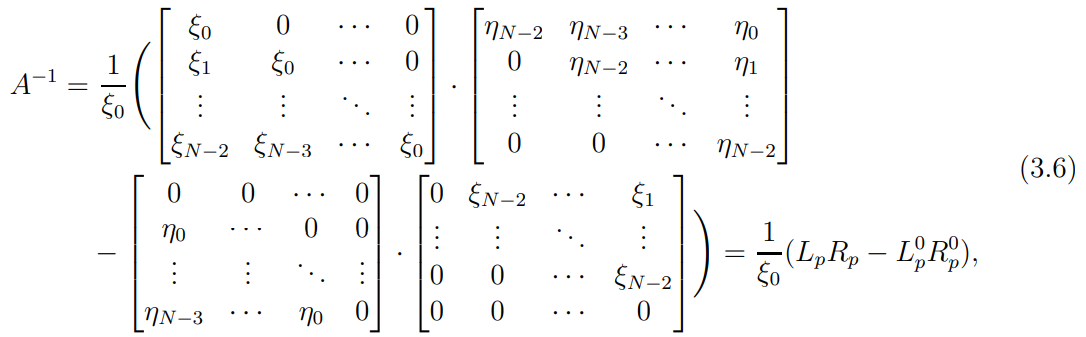 где 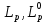 - обе нижние тёплицевы матрицы, а - обе нижние тёплицевы матрицы, а 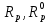 - верхние тёплицевы матрицы. Следовательно, умножение матрицы на вектор Теплица - верхние тёплицевы матрицы. Следовательно, умножение матрицы на вектор Теплица 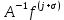 могут быть заархивированы в несколько БПФ длиной 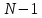 [51]. Для удобства следующий быстрый алгоритм может быть применен для вычисления произведения [51]. Для удобства следующий быстрый алгоритм может быть применен для вычисления произведения 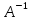 и вектора и вектора 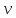 . .Алгоритм 1: вычисление 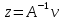 1: решите две линейные системы в уравнении. (3.5) 2: вычислить 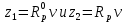 через БПФ через БПФ3: вычислить 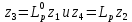 через БПФ через БПФ4: вычислить 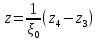 Таким образом, нам нужно найти некоторые эффективные решатели для несимметричных результирующих линейных систем Теплица, будь то решение (3.3) или решение (3.5). В следующем подразделе мы расскажем, как создавать эффективные итерационные решатели с предобуславливанием для несимметричных Теплицевых линейных систем. |
