Отчет Нартикоев. Отчет по практике Вид практики Производственная (преддипломная) практика Выполнил студент
 Скачать 0.88 Mb. Скачать 0.88 Mb.
|
4 Численные результатыВ этом разделе мы сначала проведем несколько численных экспериментов, чтобы проиллюстрировать, что предлагаемая нами IDS действительно может сходиться со вторым порядком точности как в пространстве, так и во времени. В то же время сообщается о некоторых численных примерах, демонстрирующих эффективность методов быстрого решения (то есть алгоритмов 1-3), разработанных в разделе 3. Для метода подпространства Крылова и прямого решателя мы выбираем встроенные функции для метода предобусловливания CGS (PCGS), LU-факторизации MATLAB в примере 1 и обратной косой черты MATLAB в примере 2, соответственно. Для метода CGS с циркулянтными предобуславливателями критерием остановки этих методов является 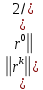 , где , где 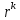 - вектор невязки линейной системы после - вектор невязки линейной системы после 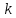 итераций, а исходное предположение выбирается в качестве нулевого вектора. итераций, а исходное предположение выбирается в качестве нулевого вектора.Пример 1 В этом примере мы рассматриваем уравнение (1.1) на пространственном интервале 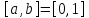 и временном интервале и временном интервале  с коэффициентами диффузии с коэффициентами диффузии 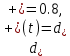 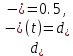 , коэффициент конвекции , коэффициент конвекции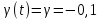 , начальное условие , начальное условие 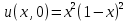 и исходный член и исходный член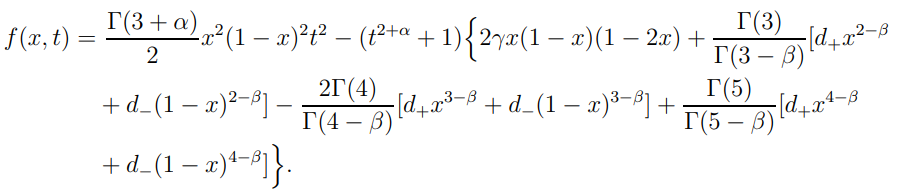 Точное решение этого примера: 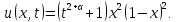 Для конечно-разностной дискретизации шаг по пространству и шаг по времени принимаются равными Для конечно-разностной дискретизации шаг по пространству и шаг по времени принимаются равными 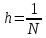 и и 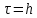 , соответственно. Ошибки ( , соответственно. Ошибки (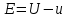 ) и порядок сходимости (ПС) в нормах ) и порядок сходимости (ПС) в нормах 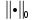 и и 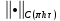 , где , где 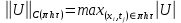 приведены в таблицах 1-2. Эти обозначения используются в этом разделе. Кроме того, эффективность методов быстрого решения, представленных в разделе 3 для этого примера, будет проиллюстрирована в таблицах 3-4. В следующих таблицах «Speed-up» определяется как приведены в таблицах 1-2. Эти обозначения используются в этом разделе. Кроме того, эффективность методов быстрого решения, представленных в разделе 3 для этого примера, будет проиллюстрирована в таблицах 3-4. В следующих таблицах «Speed-up» определяется как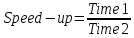 Очевидно, что, когда 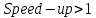 , это означает, что , это означает, что 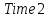 , необходимое для предлагаемого нами метода, более конкурентоспособно, чем , необходимое для предлагаемого нами метода, более конкурентоспособно, чем 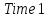 , требуемое алгоритмом 3, с повторным использованием декомпозиции LU в аспектах затраченного времени CPU. , требуемое алгоритмом 3, с повторным использованием декомпозиции LU в аспектах затраченного времени CPU.Как видно из таблицы 1, он обнаруживает, что по мере увеличения количества пространственных подинтервалов и временных шагов при сохранении 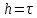 происходит уменьшение максимальной ошибки, как и ожидалось, и порядок сходимости приближенной схемы равен происходит уменьшение максимальной ошибки, как и ожидалось, и порядок сходимости приближенной схемы равен 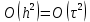 , где порядок сходимости задается формулой: , где порядок сходимости задается формулой: 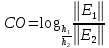 ( (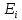 - ошибка, соответствующая - ошибка, соответствующая 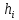 ). С другой стороны, таблица 2 показывает, что если ). С другой стороны, таблица 2 показывает, что если 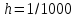 , то по мере увеличения количества временных шагов нашей приближенной схемы происходит уменьшение максимальной ошибки, как и ожидалось, и порядок сходимости по времени равен , то по мере увеличения количества временных шагов нашей приближенной схемы происходит уменьшение максимальной ошибки, как и ожидалось, и порядок сходимости по времени равен 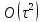 , где порядок сходимости задается следующей формулой: , где порядок сходимости задается следующей формулой: 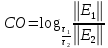 . .Во-первых, некоторые графики собственных значений исходной и предварительно обусловленной матриц нарисованы на рис. 1-2. Эти два рисунка подтверждают, что для циркулянтного предварительного кондиционирования собственные значения предварительно обусловленных матриц группируются в 1, за исключением нескольких (около 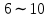 ) выбросов. Подавляющее большинство собственных значений хорошо отделены от 0. Это можно интерпретировать как то, что в нашей реализации количество итераций, требуемых для методов предобусловленного подпространства Крылова, почти колеблется от 6 до 10. Мы проверяем эффективность и надежность разработанного циркулянтного предобуславливателя с точки зрения распределения спектра кластеризации. ) выбросов. Подавляющее большинство собственных значений хорошо отделены от 0. Это можно интерпретировать как то, что в нашей реализации количество итераций, требуемых для методов предобусловленного подпространства Крылова, почти колеблется от 6 до 10. Мы проверяем эффективность и надежность разработанного циркулянтного предобуславливателя с точки зрения распределения спектра кластеризации.В таблицах 3-4 показано, что предлагаемый быстрый прямой решатель для различных дискретизированных задач требует гораздо меньше процессорного времени, затрачиваемого при увеличении 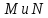 . При . При 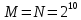 и различных дискретизированных параметрах время CPU алгоритма 3 составляет около и различных дискретизированных параметрах время CPU алгоритма 3 составляет околоТаблица 1: 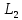 -норма и максимальная норма поведения ошибок по сравнению с уменьшением размера сетки при -норма и максимальная норма поведения ошибок по сравнению с уменьшением размера сетки при 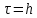 и в примере 1, и в примере 1, 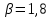 . .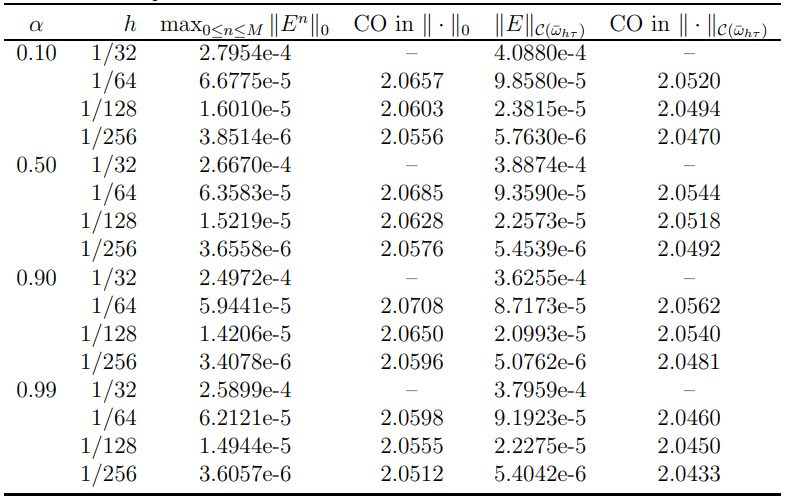 Таблица 2: Поведение ошибок 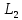 -нормы и максимальной нормы в зависимости от уменьшения размера -нормы и максимальной нормы в зависимости от уменьшения размера 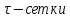 , когда , когда 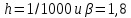 в примере 1. в примере 1.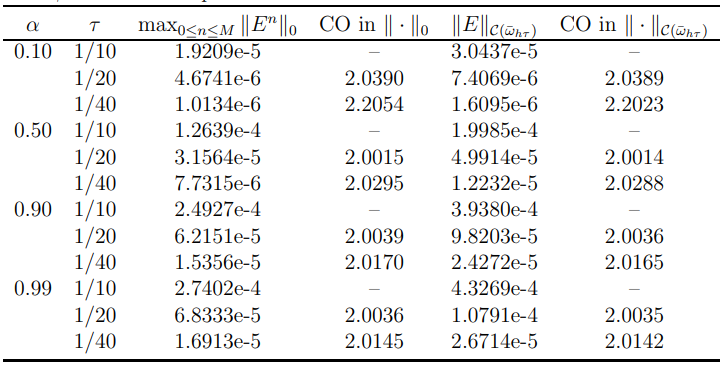 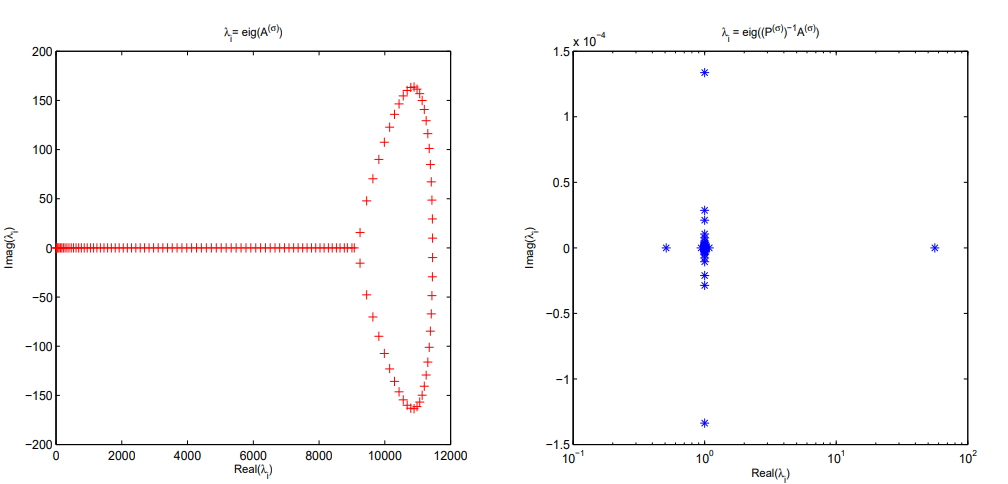 Рис. 1: Спектр исходной и предварительно обусловленной матриц на временном уровне 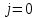 , соответственно, при , соответственно, при 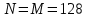 , , 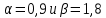 . . Слева: исходная матрица; Справа: циркулянтная предварительно обусловленная матрица. 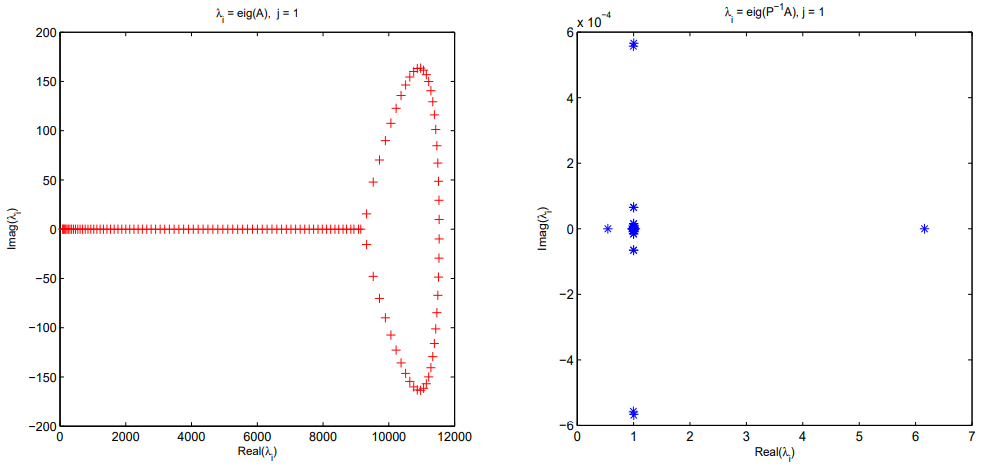 Рис. 2: Спектр исходной и предварительно обусловленной матриц на временном уровне j = 1, соответственно, при 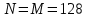 , , 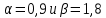 . .Слева: исходная матрица; Справа: циркулирующий предварительно обусловленная матрица. Таблица 3: Процессорное время в секундах для решения примера 1 с 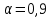 , которое выполняется Time1 для алгоритма 3 (разложение LU), а Time2 выполняется алгоритмом 3 с алгоритмом 1 , которое выполняется Time1 для алгоритма 3 (разложение LU), а Time2 выполняется алгоритмом 3 с алгоритмом 1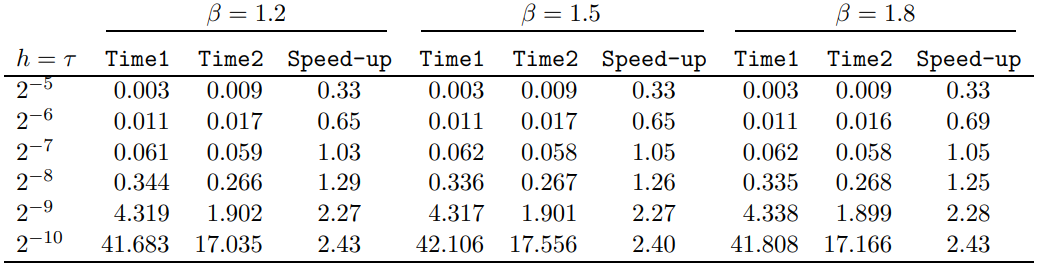 Таблица 4: Время CPU в секундах для решения примера 1 с 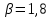 , которое выполняется Time1 для алгоритма 3 (разложение LU), а Time2 выполняется алгоритмом 3 с алгоритмом 1. , которое выполняется Time1 для алгоритма 3 (разложение LU), а Time2 выполняется алгоритмом 3 с алгоритмом 1.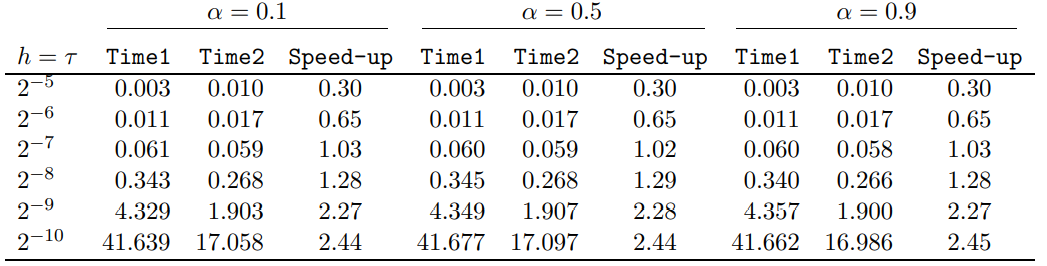 17 секунд, ускорение более чем в 2 раза. Между тем, хотя Time1 требуется алгоритмом 3 для небольших тестовых задач 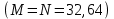 , чем Time2, необходимое для алгоритма 3, предлагаемый нами метод все же более привлекателен с точки зрения меньших требований к памяти. По сравнению с алгоритмом 3 с повторным использованием LU разложения, он отметил, что в целом реализации предложенный способ решение не требует, чтобы хранить полные матрицы (например, некоторые матрицы , чем Time2, необходимое для алгоритма 3, предлагаемый нами метод все же более привлекателен с точки зрения меньших требований к памяти. По сравнению с алгоритмом 3 с повторным использованием LU разложения, он отметил, что в целом реализации предложенный способ решение не требует, чтобы хранить полные матрицы (например, некоторые матрицы 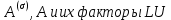 ) вообще. Короче говоря, мы можем сделать вывод, что предлагаемая нами НРС с быстрой реализацией по-прежнему более конкурентоспособна, чем НРС с повторным использованием традиционной декомпозиции LU. ) вообще. Короче говоря, мы можем сделать вывод, что предлагаемая нами НРС с быстрой реализацией по-прежнему более конкурентоспособна, чем НРС с повторным использованием традиционной декомпозиции LU.Пример 2 В этом примере мы рассматриваем уравнение (1.1) на пространственном интервале 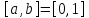 и временном интервале и временном интервале  с коэффициентами диффузии с коэффициентами диффузии 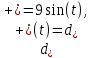 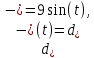 , коэффициент конвекции , коэффициент конвекции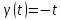 , начальное условие , начальное условие 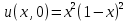 и исходный член и исходный член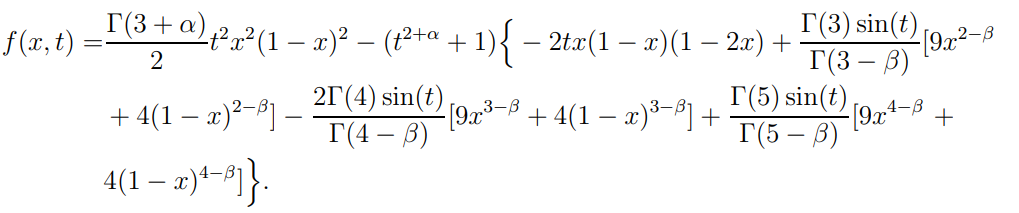 Точное решение этого примера: 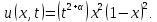 Для конечно-разностной дискретизации шаг по пространству и шаг по времени принимаются равными Для конечно-разностной дискретизации шаг по пространству и шаг по времени принимаются равными 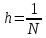 и и 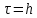 , соответственно. Результаты экспериментов с предлагаемой НРС для примера 3 указано в таблицах 5-6. Кроме того, эффективность методов быстрого решения, представленных в разделе 3 для этого примера, будет проиллюстрирована в таблицах 7-8. , соответственно. Результаты экспериментов с предлагаемой НРС для примера 3 указано в таблицах 5-6. Кроме того, эффективность методов быстрого решения, представленных в разделе 3 для этого примера, будет проиллюстрирована в таблицах 7-8.Таблица 5: Поведение  -нормы и максимальной нормы ошибки в зависимости от уменьшения размера сетки, когда -нормы и максимальной нормы ошибки в зависимости от уменьшения размера сетки, когда  в примере 2. в примере 2. Как видно из таблицы 5, он обнаруживает, что по мере увеличения количества пространственных подинтервалов и временных шагов при сохранении 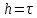 происходит уменьшение максимальной ошибки, как и ожидалось, и порядок сходимости приближенной схемы равен происходит уменьшение максимальной ошибки, как и ожидалось, и порядок сходимости приближенной схемы равен 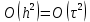 , где порядок сходимости задается формулой: , где порядок сходимости задается формулой: 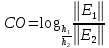 ( (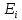 - ошибка, соответствующая - ошибка, соответствующая  ). С другой стороны, таблица 6 показывает, что если ). С другой стороны, таблица 6 показывает, что если  , то по мере увеличения количества временных шагов нашей приближенной схемы происходит уменьшение максимальной ошибки, как и ожидалось, и порядок сходимости по времени равен , то по мере увеличения количества временных шагов нашей приближенной схемы происходит уменьшение максимальной ошибки, как и ожидалось, и порядок сходимости по времени равен  , где порядок сходимости задается следующей формулой: , где порядок сходимости задается следующей формулой:  . .Таблица 6: Поведение ошибок  -нормы и максимальной нормы в зависимости от уменьшения размера τ-сетки при -нормы и максимальной нормы в зависимости от уменьшения размера τ-сетки при  в примере 2. в примере 2.  Рис. 3: Спектр исходной и предварительно обусловленной матриц на временном уровне  , соответственно, при , соответственно, при  . . Слева: исходная матрица; Справа: циркулянтная предварительно обусловленная матрица.  Рис. 4: Спектр исходной и предварительно обусловленной матриц на временном уровне  , соответственно, при , соответственно, при  . . Слева: исходная матрица; Справа: циркулянтная предварительно обусловленная матрица. Опять же, для случая переменных временных коэффициентов несколько графиков собственных значений как для исходных, так и для предварительно обусловленных матриц аналогичным образом отображаются на Рис. 3-4. Эти два рисунка подтверждают, что для циркулянтного предварительного кондиционирования собственные значения предварительно обусловленных матриц группируются в 1, за исключением нескольких (около 6 ∼ 10) выбросов. Подавляющее большинство собственных значений хорошо отделены от нуля. Это можно в основном интерпретировать как то, что в нашей реализации количество итераций, необходимых для PCGS с циркулянтными предобуславливателями, составляет почти от 6 до 10. Мы проверяем эффективность и надежность предлагаемого циркулянта прекондиционер с точки зрения кластеризации спектра. Таблица 7: Время CPUв секундах для решения примера 2 с  , которое выполняется Time1 для алгоритма 2,а Time2 выполняется алгоритмом 2 с решателем PCGS. , которое выполняется Time1 для алгоритма 2,а Time2 выполняется алгоритмом 2 с решателем PCGS. Таблица 8: Время CPU в секундах для решения примера 2 с  , которое выполняется Time1 для алгоритма 2, а Time2 выполняется алгоритмом 2 с решателем PCGS. , которое выполняется Time1 для алгоритма 2, а Time2 выполняется алгоритмом 2 с решателем PCGS. В таблицах 7-8 подтверждается, что предлагаемый быстрый прямой решатель для различных дискретизированных задач требует гораздо меньше процессорного времени, затрачиваемого при увеличении M и N. Когда  и различные дискретизированные параметры, процессорное время алгоритма 3 от PCGS с циркулянтными предобуславливателями составляет около 23 секунд, ускорение почти в 14 раз. Между тем, хотя Time1 требуется для алгоритма 3 с обратной косой чертой MATLAB для небольших тестовых задач ( и различные дискретизированные параметры, процессорное время алгоритма 3 от PCGS с циркулянтными предобуславливателями составляет около 23 секунд, ускорение почти в 14 раз. Между тем, хотя Time1 требуется для алгоритма 3 с обратной косой чертой MATLAB для небольших тестовых задач ( ), чем Time2, необходимое для алгоритма 3 с использованием метода PCGS, предлагаемый нами метод все же более привлекателен в аспектах более низких требований к памяти. ), чем Time2, необходимое для алгоритма 3 с использованием метода PCGS, предлагаемый нами метод все же более привлекателен в аспектах более низких требований к памяти. |
