Отчет Нартикоев. Отчет по практике Вид практики Производственная (преддипломная) практика Выполнил студент
 Скачать 0.88 Mb. Скачать 0.88 Mb.
|
3.2 Быстрая реализация НРС на основе предварительно подготовленного итеративного решателяВ этом подразделе мы обсудим подробную структуру реализации предложенной неявной разностной схемы (2.1). Для наглядности алгоритм решения неявной разностной схемы приведен в алгоритме 2. Алгоритм 2 Практическая реализация НРС 1:  2: вычислить 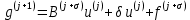 3: решить 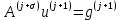 4: end for Из алгоритма 2 требуется решить M реальных линейных систем. Если применяется прямой решатель (например, метод Гаусса [60, стр. 33-44]), его погрешность будет 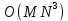 , что очень много, если N велико. Фактически, произведение матрица-вектор , что очень много, если N велико. Фактически, произведение матрица-вектор 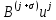 на шаге 2 может быть вычислено с помощью БПФ за O ( на шаге 2 может быть вычислено с помощью БПФ за O (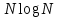 ) операций, тогда быстрые итерационные решатели Теплица интенсивно изучаются, см., [51]. Недавно они были применены для уравнения пространственной дробной диффузии [14,42,52,53,58,59]. С помощью метода подпространств Крылова с циркулянтными предобуславливателями в [53] система Теплица из пространственного уравнения дробной диффузии может быть решена с высокой скоростью сходимости. В этом случае также было отмечено, что алгоритмическая погрешность методов предобусловленных подпространств Крылова составляет всего O ( ) операций, тогда быстрые итерационные решатели Теплица интенсивно изучаются, см., [51]. Недавно они были применены для уравнения пространственной дробной диффузии [14,42,52,53,58,59]. С помощью метода подпространств Крылова с циркулянтными предобуславливателями в [53] система Теплица из пространственного уравнения дробной диффузии может быть решена с высокой скоростью сходимости. В этом случае также было отмечено, что алгоритмическая погрешность методов предобусловленных подпространств Крылова составляет всего O (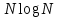 ) арифметических операций на шаг итерации. Руководствуясь приведенными выше соображениями, мы сначала реализуем умножение матрицы на вектор ) арифметических операций на шаг итерации. Руководствуясь приведенными выше соображениями, мы сначала реализуем умножение матрицы на вектор 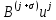 на первом шаге алгоритма 2 с помощью БПФ. Затем решение линейных систем Теплица на первом шаге алгоритма 2 с помощью БПФ. Затем решение линейных систем Теплица 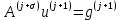 на шаге 3 методами подпространства Крылова, например, методом квадратов сопряженных градиентов [55, с. 241- 244], с циркулянтными прекондитонатором на шаге 3 методами подпространства Крылова, например, методом квадратов сопряженных градиентов [55, с. 241- 244], с циркулянтными прекондитонатором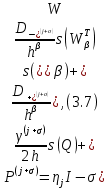 где s (·) означает хорошо известное циркулянтное приближение Стрэнга для данной Теплицевой матрицы [51, 53]. Высокая эффективность предкондиционера циркулянта Стрэнга для космических ФДУ подтверждена в [53]. Чтобы убедиться, что предобуславливатель, определенный в (3.7), корректно определен, проиллюстрируем, что 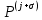 не особые не особыеЛемма 3.1 Все собственные значения 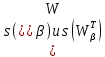 попадают внутрь открытого диска попадают внутрь открытого диска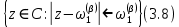 Доказательство. Весь круг Гершгорина [55, с. 119-122] циркулянтных матриц 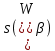 и и 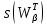 центрирован в точке центрирован в точке 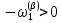 с радиусом с радиусом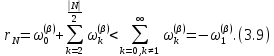 по свойствам последовательности { 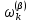 }; см. лемму 2.3 и лемму 2.4. }; см. лемму 2.3 и лемму 2.4.Замечание 3.1 Стоит отметить, что: Действительные части всех собственных значений 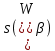 и и 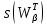 строго отрицательны для всех строго отрицательны для всех 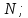 Модули всех собственных значений 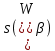 и и 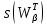 ограничены сверху величиной ограничены сверху величиной 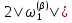 для всех для всех 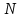 . .Как известно, циркулянтную матрицу можно быстро диагонализовать с помощью матрицы Фурье F [21, 51, 53]. Тогда следует, что 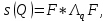 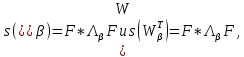 где где 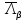 - комплексно-сопряженное к - комплексно-сопряженное к 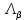 . Разложите циркулянтную матрицу . Разложите циркулянтную матрицу 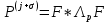 с диагональной матрицей с диагональной матрицей 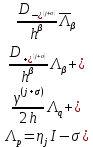 . Тогда . Тогда 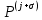 обратимо, если все диагональные элементы Λp ненулевые. Более того, мы можем получить следующий вывод об обратимости обратимо, если все диагональные элементы Λp ненулевые. Более того, мы можем получить следующий вывод об обратимости 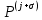 в (3.7). в (3.7).Теорема 3.1 Циркулянтные предобуславливатели 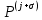 определенные в (3.7), неособые. определенные в (3.7), неособые.Доказательство. Прежде всего, мы уже знаем, что 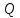 - кососимметричная матрица Теплица, она также обнаруживает, что - кососимметричная матрица Теплица, она также обнаруживает, что 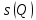 также является кососимметричной циркулянтной матрицей, поэтому действительная часть также является кососимметричной циркулянтной матрицей, поэтому действительная часть 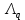 равна нулю, т.е. равна нулю, т.е. 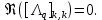 С другой стороны, согласно части 1 замечания 3.1 имеем С другой стороны, согласно части 1 замечания 3.1 имеем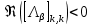 . Отмечая, что . Отмечая, что 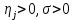 , и , и 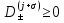 , таким образом, мы получаем , таким образом, мы получаем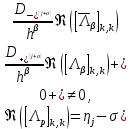 для каждого 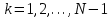 . Следовательно, . Следовательно, 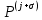 обратимы. обратимы.Здесь, хотя мы не планируем теоретически исследовать собственные значения распределения матриц, предварительно 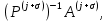 мы можем дать некоторые цифры для иллюстрации кластеризации собственных значений распределения нескольких заданных матриц, предварительно в следующем разделе. Кроме того, наши численные эксперименты показывают, что количество итераций всегда колеблется от 6 до 10, поэтому мы рассматриваем погрешность решения линейной системы на шаге 3 как мы можем дать некоторые цифры для иллюстрации кластеризации собственных значений распределения нескольких заданных матриц, предварительно в следующем разделе. Кроме того, наши численные эксперименты показывают, что количество итераций всегда колеблется от 6 до 10, поэтому мы рассматриваем погрешность решения линейной системы на шаге 3 как 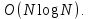 Это также означает, что вычислительная погрешность для реализации всей НРС составляет около Это также означает, что вычислительная погрешность для реализации всей НРС составляет около 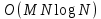 операций. операций.Кроме того, если у нас есть коэффициенты 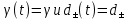 в уравнении. (1.1) матрица в уравнении. (1.1) матрица 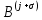 также имеет тот же вид, что и также имеет тот же вид, что и 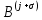 в уравнении. (3.4), то мы можем упростить алгоритм 2 до следующего алгоритма 3. в уравнении. (3.4), то мы можем упростить алгоритм 2 до следующего алгоритма 3.Опять же, если использовать прямой метод для решения линейной системы на шаге 4 и вычисления обратной матрицы 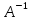 с помощью LU-разложения, которое можно повторно использовать на шаге 7 алгоритма 3, но его погрешность будет по-прежнему с помощью LU-разложения, которое можно повторно использовать на шаге 7 алгоритма 3, но его погрешность будет по-прежнему 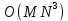 , что очень много, если N большое. , что очень много, если N большое.Заметим, что в шагах 3, 4, 6 и 7 алгоритма 3, структура Теплица из этих четырех матриц не были использованы при решении линейной системы. Фактически, два умножения матрицы на вектор 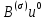 и и 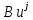 на шагах 3 и 6 могут быть вычислены как на шагах 3 и 6 могут быть вычислены какАлгоритм 3 Практическая реализация НРС с постоянными коэффициентами 1:  2: 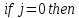 3: Вычислить 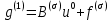 4: Решить 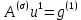 5: 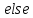 6: Вычислить 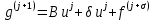 7: Решить 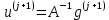 8: 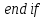 9: 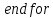 БПФ за 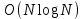 операций, затем быстрые итерационные решатели Тплица с подходящими контурными предобуславливателями, система Тплица на шаге 4 и (3.5) может быть решена с высокой скоростью сходимости. Здесь мы можем построить два циркулянтных предобуславливателя, определяемых как операций, затем быстрые итерационные решатели Тплица с подходящими контурными предобуславливателями, система Тплица на шаге 4 и (3.5) может быть решена с высокой скоростью сходимости. Здесь мы можем построить два циркулянтных предобуславливателя, определяемых как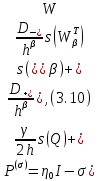 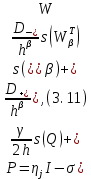 для линейных систем из шага 4 и (3.5) соответственно. Здесь обратимость указанных выше двух циркулянтных предобуславливателей, введенных в (3.10) - (3.11), может быть аналогичным образом заархивирована с помощью теоремы 3.1. Затем мы можем использовать алгоритм 1 для вычисления умножения матрицы на вектор 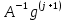 на шаге 7 алгоритма 3. Аналогичным образом, согласно результатам в следующем разделе, мы обнаруживаем, что числа итераций, требуемые для методов предварительно обусловленных подпространств Крылова, всегда колеблются от 6 до 10. В этом случае также примечательно, что алгоритмическая погрешность методов предобусловленных подпространств Крылова составляет всего на шаге 7 алгоритма 3. Аналогичным образом, согласно результатам в следующем разделе, мы обнаруживаем, что числа итераций, требуемые для методов предварительно обусловленных подпространств Крылова, всегда колеблются от 6 до 10. В этом случае также примечательно, что алгоритмическая погрешность методов предобусловленных подпространств Крылова составляет всего 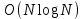 на каждой итерации. В заключение, общая сложность реализации НРС с постоянными коэффициентами также составляет на каждой итерации. В заключение, общая сложность реализации НРС с постоянными коэффициентами также составляет 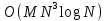 . . |
