Отчет Нартикоев. Отчет по практике Вид практики Производственная (преддипломная) практика Выполнил студент
 Скачать 0.88 Mb. Скачать 0.88 Mb.
|
Неявная разностная схемаВ этом разделе мы представляем неявный разностный метод дискретизации ПВДУКД, определенный в (1). В отличие от прежних численных подходов с точностью первого порядка как по времени, так и по пространству [37–39,41,42], в дальнейшем мы будем использовать двусторонние дробные производные для аппроксимации производных Римана-Лиувилля в (1.3) и (1.4). Мы можем показать, что с помощью двусторонних дробных производных этот предложенный метод также безусловно устойчив и сходится во втором порядке точности во времени и пространстве. 2.1 Численная дискретизация ПВДУКДДля вывода предложенной схемы введем сначала некоторые обозначения. В прямоугольник 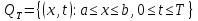 мы вводим сетку мы вводим сетку 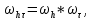 тогда тогда 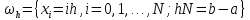 , и , и 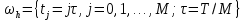 . Кроме, . Кроме, 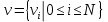 любая сеточная функция. Затем следующая лемма, введенная в [56], дает описание дискретизации по времени. любая сеточная функция. Затем следующая лемма, введенная в [56], дает описание дискретизации по времени.Лемма 2.1 Предполагаем 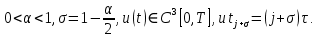 Тогда Тогда 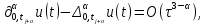 где 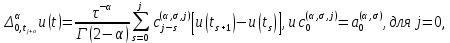 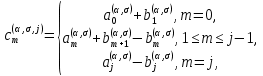 для 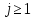 , в котором , в котором 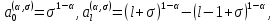 для для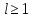 ; и ; и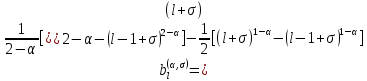 . .Обозначим 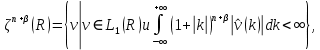 где где 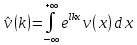 - преобразование Фурье функции - преобразование Фурье функции 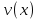 , и мы используем , и мы используем 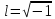 для обозначения мнимой единицы. Для дискретизации по пространству введем следующую лемму: для обозначения мнимой единицы. Для дискретизации по пространству введем следующую лемму:Лемма 2.2 Предполагаем, 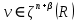 и пусть и пусть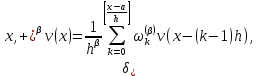 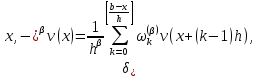 тогда для фиксированного 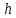 , мы имеем , мы имеем 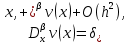 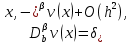 где 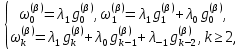 c 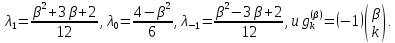 Пусть 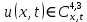 решение задачи (1). Рассмотрим уравнение (1) для решение задачи (1). Рассмотрим уравнение (1) для 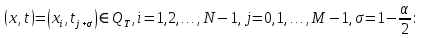 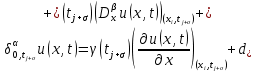 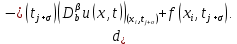 Для простоты введем обозначения 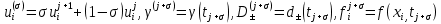 и 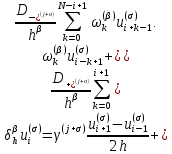 Затем с учетом леммы 2.1 выводится неявная разностная схема с порядком аппроксимации O ( 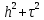 ): ):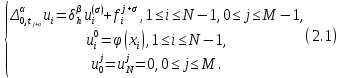 Интересно отметить, что при 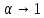 мы получаем разностную схему Кранка – Николсона. мы получаем разностную схему Кранка – Николсона.2.2 Анализ неявной разностной схемыВ этом разделе мы анализируем устойчивость и сходимость неявной разностной схемы (2.1). Пусть  Для 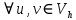 определим дискретное скалярное произведение и соответствующую дискретную норму L2 следующим образом: определим дискретное скалярное произведение и соответствующую дискретную норму L2 следующим образом: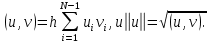 Приведем несколько лемм для доказательства устойчивости и сходимости неявной разностной схемы (2.1). Лемма 2.3 ([9, 52, 57]) Пусть 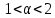 и и 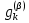 определена в лемме 2.2. Тогда мы имеем определена в лемме 2.2. Тогда мы имеем 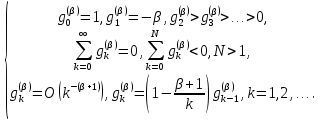 Лемма 2.4 ([57,58]) Пусть 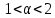 и и 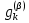 определена в лемме 2.2. Тогда мы имеем определена в лемме 2.2. Тогда мы имеем 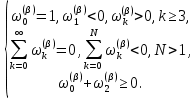 Лемма 2.5 ([57,58]) Для 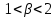 , и любого , и любого 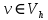 , выполняется , выполняется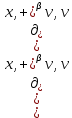 Лемма 2.6 Для 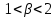 , и любого , и любого 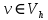 , выполняется существует положительная постоянная , выполняется существует положительная постоянная 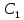 , такой, что , такой, что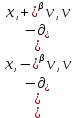 Доказательство. 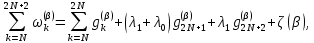 где 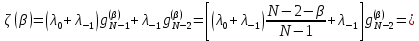 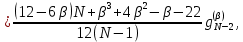 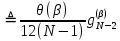 тогда 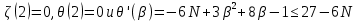 , что подразумевает , что подразумевает 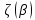 убывающая функция для убывающая функция для 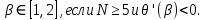 Следовательно Следовательно 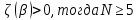 . .Тогда по лемме 2.3 существуют положительные постоянные 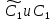 такие, что такие, что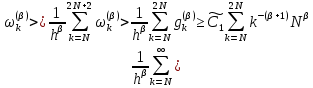 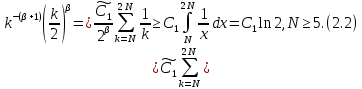 Тогда, используя леммы 2.4 и 2.5, получаем 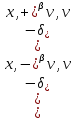 что доказывает лемму. На основе приведенных выше лемм можно получить следующую теорему, существенную для анализа устойчивости предложенной неявной разностной схемы Теорема 2.1 Для любого 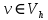 , выполняется , выполняется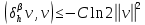 где 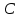 - положительная постоянная, не зависящая от размера шага в пространстве - положительная постоянная, не зависящая от размера шага в пространстве 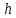 . .Доказательство. Конкретное выражение 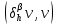 можно записать как можно записать как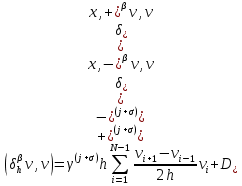 Отметим, что 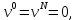 получим получим 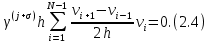 Более того, согласно лемме 2.6 существует положительная константа 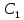 , не зависящая от размера шага , не зависящая от размера шага 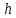 по пространству, такая, что для любого ненулевого вектора по пространству, такая, что для любого ненулевого вектора 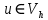 получаем получаем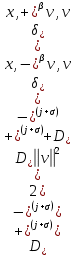 Пусть 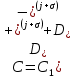 . Подставляя (2.4) и (2.5) в (2.3), справедлива Теорема 2.1. . Подставляя (2.4) и (2.5) в (2.3), справедлива Теорема 2.1.Лемма 2.7 ([56,58]) Пусть 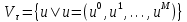 для любого для любого 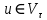 ; имеет место следующее неравенство ; имеет место следующее неравенство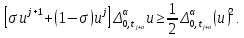 Теперь можно сделать вывод об устойчивости и сходимости неявной разностной схемы (2.1). Для простоты изложения в нашем доказательстве мы обозначаем 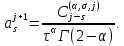 Тогда Тогда 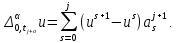 Теорема 2.2 Обозначим 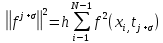 . Тогда неявная разностная схема (2.1) безусловно устойчива и справедлива следующая априорная оценка: . Тогда неявная разностная схема (2.1) безусловно устойчива и справедлива следующая априорная оценка: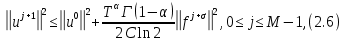 где 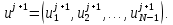 Доказательство. Чтобы скалярно произведение (2.1) на 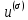 , мы имеем , мы имеем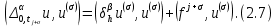 Из теоремы 2.1 и леммы 2.6 следует, что 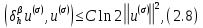 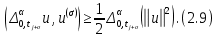 Подставляя (2.8) - (2.9) в (2.7) и используя неравенство Коши-Шварца, получаем 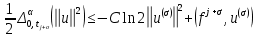 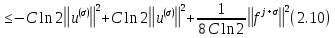 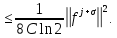 Далее, он утверждает, что 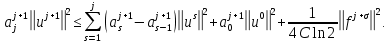 где 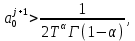 получим получим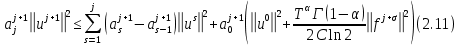 Предположим, что 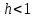 , и обозначим , и обозначим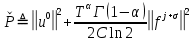 Тогда уравнение. (2.11) можно переписать как 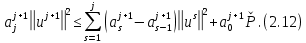 Далее докажем справедливость оценочного соотношения (2.6) 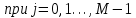 по математической индукции. Очевидно, что из (2.12) следует, что (2.6) выполняется при j = 0. Предположим, что неравенство (2.6) имеет место для всех по математической индукции. Очевидно, что из (2.12) следует, что (2.6) выполняется при j = 0. Предположим, что неравенство (2.6) имеет место для всех 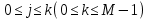 , то есть , то есть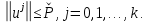 Для (2.12) при j = k имеем 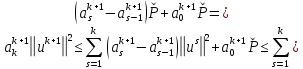 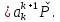 Доказательство теоремы 2.2 полностью завершено. Теорема 2.3 Предположим, что 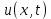 - решение (1.1), а - решение (1.1), а 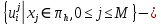 решение неявной разностной схемы (2.1). Обозначить решение неявной разностной схемы (2.1). Обозначить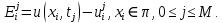 Тогда существует положительная постоянная 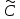 такая, что такая, что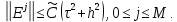 Доказательство Он может легко получить, что 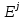 удовлетворяет следующее уравнение ошибки удовлетворяет следующее уравнение ошибки 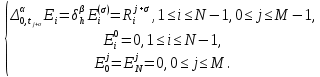 где 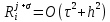 . Используя теорему 2.2, получаем . Используя теорему 2.2, получаем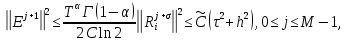 что доказывает теорему. |
