Отчет Нартикоев. Отчет по практике Вид практики Производственная (преддипломная) практика Выполнил студент
 Скачать 0.88 Mb. Скачать 0.88 Mb.
|
ЗаключениеВ статье исследуется устойчивость и сходимость неявных разностных схем, аппроксимирующих пространственно-временное дробное уравнение конвекции-диффузии общего вида. Получены достаточные условия безусловной устойчивости таких разностных схем. Для доказательства устойчивости широкого класса разностных схем, аппроксимирующих уравнение дробной диффузии по времени, достаточно просто проверить условия устойчивости, полученные в данной статье. Между тем, новые разностные схемы второго построены также порядок аппроксимации по пространству и второй порядок аппроксимации по времени для ПВДУКД с переменными коэффициентами (в терминах t). Доказана устойчивость и сходимость этих неявных схем в сеточной L2-норме со скоростью, равной порядку ошибки аппроксимации. Метод может быть легко адаптирован к другим ПВДУКД с другими граничными условиями. Проведены численные испытания, полностью подтверждающие полученные теоретические результаты. Что еще более важно, с помощью (3.1) мы можем улучшить навыки вычислений за счет реализации надежных итерационных методов предварительного кондиционирования, с только вычислительными затратами и памятью в размере O ( 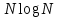 ) и O ( ) и O (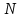 ), соответственно. Обширные численные результаты сообщаются, чтобы проиллюстрировать эффективность предлагаемых методов предварительного кондиционирования. В будущей работе мы сосредоточимся на расширении предлагаемой НРС для обработки двух / трех - мерных ПВДУКД с помощью методов быстрого решения с учетом различных граничных значений. Между тем, мы также сосредоточимся на разработке других эффективных предобуславливателями для ускорения сходимости решателя подпространств Крылова для дискретизированных. ), соответственно. Обширные численные результаты сообщаются, чтобы проиллюстрировать эффективность предлагаемых методов предварительного кондиционирования. В будущей работе мы сосредоточимся на расширении предлагаемой НРС для обработки двух / трех - мерных ПВДУКД с помощью методов быстрого решения с учетом различных граничных значений. Между тем, мы также сосредоточимся на разработке других эффективных предобуславливателями для ускорения сходимости решателя подпространств Крылова для дискретизированных. Список литературы[1] I. Podlubny, Fractional Differential Equations, vol. 198 of Mathematics in Science and Engineering, Academic Press, Inc., San Diego, CA, 1999. [2] S.G. Samko, A.A. Kilbas, O.I. Marichev, Fractional Integrals and Derivatives: Theory and Applications, Gordon and Breach Science Publishers, Yverdonn, 1993. [3] A.A. Kilbas, H.M. Srivastava, J.J. Trujillo, Theory and Applications of Fractional Differential Equations, Elsevier, Amsterdam, 2006. [4] R. Metzler, J. Klafter, The random walk’s guide to anomalous diffusion: a fractional dynamics approach, Phys. Rep., 339 (2000), pp. 1-77. [5] A.I. Saichev, G.M. Zaslavsky, Fractional kinetic equations: solutions and applications, Chaos, 7 (1997), pp. 753-764. Available online at http://dx.doi.org/10.1063/1.166272. [6] Y. Povstenko, Space-time-fractional advection diffusion equation in a plane, in Advances in Modelling and Control of Non-integer-Order Systems, K.J. Latawiec, M. Lukaniszyn, R. Stanis lawski eds., Volume 320 of the series Lecture Notes in Electrical Engineering, Springer, 2015, pp. 275-284. [7] D.A. Benson, S.W. Wheatcraft, M.M. Meerschaert, Application of a fractional advection-dispersion equation, Water Resour. Res., 36 (2000), pp. 1403-1412. [8] Y.Z. Povstenko, Fundamental solutions to time-fractional advection diffusion equation in a case of two space variables, Math. Probl. Eng., 2014 (2014), Article ID 705364, 7 pages. Available online at http://dx.doi.org/10.1155/2014/705364. [9] M.M. Meerschaert, C. Tadjeran, Finite difference approximations for fractional advection-dispersion flow equations, J. Comput. Appl. Math., 172 (2004), pp. 65- 77. [10] L. Su, W. Wang, Q. Xu, Finite difference methods for fractional dispersion equations, Appl. Math. Comput., 216 (2010), pp. 3329-3334. [11] L. Su, W. Wang, Z. Yang, Finite difference approximations for the fractional advection-diffusion equation, Phys. Lett. A, 373 (2009), pp. 4405-4408. [12] E. Sousa, Finite difference approximations for a fractional advection diffusion problem, J. Comput. Phys., 228 (2009), pp. 4038-4054. [13] L. Su, W. Wang, H. Wang, A characteristic difference method for the transient fractional convection-diffusion equations, Appl. Numer. Math., 61 (2011), pp. 946- 960. [14] K. Wang, H. Wang, A fast characteristic finite difference method for fractional advection-diffusion equations, Adv. Water Resour., 34 (2011), pp. 810-816. [15] Z. Deng, V. Singh, L. Bengtsson, Numerical solution of fractional advection-dispersion equation, J. Hydraul. Eng., 130 (2004), pp. 422-431. [16] Z. Ding, A. Xiao, M. Li, Weighted finite difference methods for a class of space fractional partial differential equations with variable coefficients, J. Comput. Appl. Math., 233 (2010), pp. 1905-1914. [17] F. Liu, P. Zhuang, K. Burrage, Numerical methods and analysis for a class of fractional advection-dispersion models, Comput. Math. Appl., 64 (2012), pp. 2990-3007. [18] S. Momani, A.A. Rqayiq, D. Baleanu, A nonstandard finite difference scheme for two-sided space-fractional partial differential equations, Int. J. Bifurcat. Chaos, 22 (2012), 1250079, 5 pages. Available online at http://dx.doi.org/10.1142/S0218127412500794. [19] M. Chen, W. Deng, A second-order numerical method for two-dimensional two-sided space fractional convection diffusion equation, Appl. Math. Model., 38 (2014), pp. 3244-3259. [20] W. Deng, M. Chen, Efficient numerical algorithms for three-dimensional fractional partial differential equations, J. Comp. Math., 32 (2014), pp. 371-391. [21] W. Qu, S.-L. Lei, S.-W. Vong, Circulant and skew-circulant splitting iteration for fractional advection-diffusion equations, Int. J. Comput. Math., 91 (2014), pp. 2232- 2242. [22] N.J. Ford, K. Pal, Y. Yan, An algorithm for the numerical solution of two-sided space-fractional partial differential equations, Comput. Methods Appl. Math., 15 (2015), pp. 497-514. [23] A.H. Bhrawy, D. Baleanu, A spectral Legendre-Gauss-Lobatto collocation method for a space-fractional advection diffusion equations with variable coefficients, Rep. Math. Phys., 72 (2013), pp. 219-233. [24] A.H. Bhrawy, M.A. Zaky, A method based on the Jacobi tau approximation for solving multi-term time-space fractional partial differential equations, J. Comput. Phys., 281 (2015), pp. 876-895. [25] H. Hejazi, T. Moroney, F. Liu, Stability and convergence of a finite volume method for the space fractional advection-dispersion equation, J. Comput. Appl. Math., 255 (2014), pp. 684-697. [26] W.Y. Tian, W. Deng, Y. Wu, Polynomial spectral collocation method for space fractional advection-diffusion equation, Numerical Methods for Partial Differential Equations, 30 (2014), pp. 514-535. [27] Y. Lin, C. Xu, Finite difference/spectral approximations for the time-fractional diffusion equation, J. Comput. Phys., 225 (2007), pp. 1533-1552. [28] M. Cui, A high-order compact exponential scheme for the fractional convection-diffusion equation, J. Comput. Appl. Math., 255 (2014), pp. 404-416. [29] M. Cui, Compact exponential scheme for the time fractional convection-diffusion reaction equation with variable coefficients, J. Comput. Phys., 280 (2015), pp. 143- 163. [30] A. Mohebbi, M. Abbaszadeh, Compact finite difference scheme for the solution of time fractional advection-dispersion equation, Numer. Algorithms, 63 (2013), pp. 431-452. [31] S. Momani, An algorithm for solving the fractional convection-diffusion equation with nonlinear source term, Commun. Nonlinear Sci. Numer. Simul., 12 (2007), pp. 1283-1290. [32] Z. Wang, S. Vong, A high-order exponential ADI scheme for two-dimensional time fractional convection-diffusion equations, Comput. Math. Appl., 68 (2014), pp. 185- 196. [33] Z.-J. Fu, W. Chen, H.-T. Yang, Boundary particle method for Laplace transformed time fractional diffusion equations, J. Comput. Phys., 235 (2013), pp. 52-66. [34] S. Zhai, X. Feng, Y. He, An unconditionally stable compact ADI method for threedimensional time-fractional convection-diffusion equation, J. Comput. Phys., 269 (2014), pp. 138-155. [35] P. Zhuang, Y.T. Gu, F. Liu, I. Turner, P.K.D.V. Yarlagadda, Time-dependent fractional advection-diffusion equations by an implicit MLS meshless method, Int. J. Numer. Meth. Eng., 88 (2011), pp. 1346-1362. [36] Y.-M. Wang, A compact finite difference method for solving a class of time fractional convection-subdiffusion equations, BIT, 55 (2015), pp. 1187-1217. [37] Y. Zhang, A finite difference method for fractional partial differential equation, Appl. Math. Comput., 215 (2009), pp. 524-529. [38] Y. Zhang, Finite difference approximations for space-time fractional partial differential equation, J. Numer. Math., 17 (2009), pp. 319-326. [39] Y. Shao, W. Ma, Finite difference approximations for the two-side space-time fractional advection-diffusion equations, J. Comput. Anal. Appl., 21 (2016), pp. 369-379. [40] P. Qin, X. Zhang, A numerical method for the space-time fractional convectiondiffusion equation, Math. Numer. Sin., 30 (2008), pp. 305-310. (in Chinese) [41] F. Liu, P. Zhuang, V. Anh, I. Turner, K. Burrage, Stability and convergence of the difference methods for the space-time fractional advection-diffusion equation, Appl. Math. Comput., 191 (2007), pp. 12-20. [42] Z. Zhao, X.-Q. Jin, M.M. Lin, Preconditioned iterative methods for space-time fractional advection-diffusion equations, J. Comput. Phys., 319 (2016), pp. 266-279. [43] S. Shen, F. Liu, V. Anh, Numerical approximations and solution techniques for the space-time Riesz-Caputo fractional advection-diffusion equation, Numer. Algorithms, 56 (2011), pp. 383-403. [44] M. Parvizi, M.R. Eslahchi, M. Dehghan, Numerical solution of fractional advectiondiffusion equation with a nonlinear source term, Numer. Algorithms, 68 (2015), pp. 601-629. [45] Y. Chen, Y. Wu, Y. Cui, Z. Wang, D. Jin, Wavelet method for a class of fractional convection-diffusion equation with variable coefficients, J. Comput. Sci., 1 (2010), pp. 146-149. [46] S. Irandoust-pakchin, M. Dehghan, S. Abdi-mazraeh, M. Lakestani, Numerical solution for a class of fractional convection-diffusion equations using the flatlet oblique multiwavelets, J. Vib. Control, 20 (2014), pp. 913-924. [47] A.H. Bhrawy, M.A. Zaky, J.A. Tenreiro Machado, Efficient Legendre spectral tau algorithm for solving the two-sided space-time Caputo fractional advection-dispersion equation, J. Vib. Control, 22 (2016), pp. 2053-2068. [48] H. Hejazi, T. Moroney, F. Liu, A finite volume method for solving the two-sided time-space fractional advection-dispersion equation, Cent. Eur. J. Phys., 11 (2013), pp. 1275-1283. [49] W. Jiang, Y. Lin, Approximate solution of the fractional advection-dispersion equation, Comput. Phys. Commun., 181 (2010), pp. 557-561. [50] J. Wei, Y. Chen, B. Li, M. Yi, Numerical solution of space-time fractional convectiondiffusion equations with variable coefficients using Haar wavelets, Comput. Model. Eng. Sci. (CMES), 89 (2012), pp. 481-495. [51] M. Ng, Iterative Methods for Toeplitz Systems, Oxford University Press, New York, 2004. [52] F.-R. Lin, S.-W. Yang, X.-Q. Jin, Preconditioned iterative methods for fractional diffusion equation, J. Comput. Phys., 256 (2014), pp. 109-117. [53] S.-L. Lei, H.-W. Sun, A circulant preconditioner for fractional diffusion equations, J. Comput. Phys., 242 (2013), pp. 715-725. [54] I. Gohberg, A. Semencul, On the inversion of finite Toeplitz matrices and their continuous analogues, Matem. Issled., 7 (1972), pp. 201-223. (in Russian) [55] Y. Saad, Iterative Methods for Sparse Linear Systems, 2nd edition, SIAM, Philadelphia, USA, 2003. [56] A.A. Alikhanov, A new difference scheme for the time fractional diffusion equation, J. Comput. Phys., 280 (2015), pp. 424-438. [57] Z.-P. Hao, Z.-Z. Sun, W.-R. Cao, A fourth-order approximation of fractional derivatives with its applications, J. Comput. Phys., 281 (2015), pp. 787-805. [58] S. Vong, P. Lyu, X. Chen, S.-L. Lei, High order finite difference method for time-space fractional differential equations with Caputo and Riemann-Liouville derivatives, Numer. Algorithms, 72 (2016), pp. 195-210. [59] X.-M. Gu, T.-Z. Huang, H.-B. Li, L. Li, W.-H. Luo, On k-step CSCS-based polynomial preconditioners for Toeplitz linear systems with application to fractional diffusion equations, Appl. Math. Lett., 42 (2015), pp. 53-58. [60] ˚A. Bj¨orck, Direct Methods for Linear Systems, in Numerical Methods in Matrix Computations, Volume 59 of the series Texts in Applied Mathematics, Springer, Switzerland, 2014, pp. 1-209. |
