Отчет Нартикоев. Отчет по практике Вид практики Производственная (преддипломная) практика Выполнил студент
 Скачать 0.88 Mb. Скачать 0.88 Mb.
|
|
ФГБОУ ВО «СЕВЕРО-ОСЕТИНСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ИМЕНИ К.Л. ХЕТАГУРОВА» Факультет математики и информационных технологий Кафедра прикладной математики Отчет по практике Вид практики: Производственная (преддипломная) практика» Выполнил студент Нартикоев Николай Ботазович (фамилия, имя, отчество) направление подготовки 01.04.02 Прикладная математика и информатика, профиль «Математическое и информационное обеспечение экономической деятельности» Подпись студента: _____________ Дата сдачи отчета: «___» ______________20__г. Отчет принят: ___________________ _____________________________________________ подпись Ф.И.О. ответственного лица, должность «___» _______________20 __ г. Оценка __________________________ ________________/__________________________ подпись / Ф.И.О. преподавателя-экзаменатора «___» _____________20__г. ВведениеВ этой статье мы хотим предложить практические численные методы решения класса начально-краевой задачи пространственно-временных дробных уравнений конвекции-диффузии. Начнем с неявного разностного метода, основанного на двухстороннем средневзвешенным сдвигом формулы Грюнвальда предлагаются с обсуждением устойчивость и сходимость. Мы строим неявную разностную схему и показываем, что она сходится со вторым порядком точности как во времени, так и в пространстве. Затем мы разрабатываем быстрые методы решения полученной системы линейных уравнений с матрицей Теплица. Быстрые решатели подпространств Крылова с подходящими циркулянтными предобуславливателями предназначены для работы с результирующей линейной системой Теплица. Каждый временной уровень этих методов снижает требования к памяти для предлагаемой неявной разностной схемы с O ( 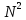 ) до O ( ) до O (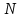 ) и вычислительную сложность с O ( ) и вычислительную сложность с O (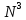 ) до O ( ) до O (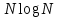 ) на каждом итерационном шаге, где N равно количество узлов сетки. Обширные численные примеры показывают полезность этих методов по сравнению с традиционными прямыми решателями неявных разностных методов с точки зрения вычислительных затрат и требований к памяти. ) на каждом итерационном шаге, где N равно количество узлов сетки. Обширные численные примеры показывают полезность этих методов по сравнению с традиционными прямыми решателями неявных разностных методов с точки зрения вычислительных затрат и требований к памяти.В последние годы растет интерес к области дробного исчисления. Подлубный [1], Самко и др. [2] и Килбас и др. [3] предоставляют историю и всестороннее рассмотрение этого предмета. Многие явления в технике, физике, химии и другие науки могут быть очень успешно описаны с помощью дробно-дифференциальных уравнений. В броуновском случае диффузия с дополнительным полем скорости и диффузия под действием постоянного внешнего силового поля моделируются уравнением конвекции-дисперсии. В случае аномальной диффузии это уже неверно, т.е. дробное обобщение может быть различным для случая адвекции и переноса внешнего силового поля в [4]. В исследовании нас очень интересует быстрый решатель для решения начально-краевой задачи пространственно-временной дробной конвекции-диффузии уравнение [5, 6]: 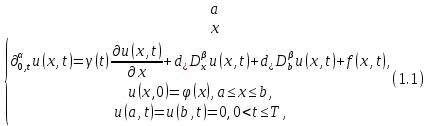 где 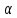 ∈ (0, 1], ∈ (0, 1], 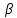 ∈ (1, 2], ∈ (1, 2], 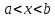 и, и, 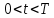 . Здесь параметры . Здесь параметры 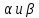 – порядка пространственно-временных дробных уравнений конвекции-диффузии, – порядка пространственно-временных дробных уравнений конвекции-диффузии, 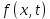 - истоковый член, а функции коэффициента диффузии - истоковый член, а функции коэффициента диффузии 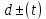 неотрицательны в предположении, что поток идет слева направо. Более того, переменные коэффициенты неотрицательны в предположении, что поток идет слева направо. Более того, переменные коэффициенты 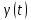 действительны. Пространственно-временные дробные уравнения конвекции-диффузии можно рассматривать как обобщение классических уравнений конвекции-диффузии с заменой производной по времени первого порядка на дробную производную Капуто порядка действительны. Пространственно-временные дробные уравнения конвекции-диффузии можно рассматривать как обобщение классических уравнений конвекции-диффузии с заменой производной по времени первого порядка на дробную производную Капуто порядка 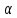 ∈ (0, 1], а производные по пространству второго порядка заменены двухсторонняя дробная производная Риммана – Лиувилля порядка ∈ (0, 1], а производные по пространству второго порядка заменены двухсторонняя дробная производная Риммана – Лиувилля порядка 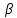 ∈ (1, 2]. А именно, дробная производная по времени в (1.1) есть дробная дробь Капуто производная порядка ∈ (1, 2]. А именно, дробная производная по времени в (1.1) есть дробная дробь Капуто производная порядка 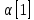 , обозначаемая , обозначаемая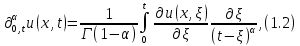 а левая ( 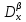 ) и правая ( ) и правая (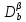 ) пространственные дробные производные в (1.1) являются дробными производными Римана-Лиувилля порядка ) пространственные дробные производные в (1.1) являются дробными производными Римана-Лиувилля порядка 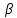 [2, 3], которые определяются формулами [2, 3], которые определяются формулами 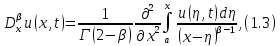 и 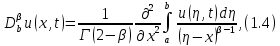 где Γ (·) обозначает гамма-функцию. Действительно, когда 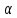 = 1 и = 1 и 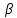 = 2, приведенное выше уравнение сводится к классическому уравнению конвекции-диффузии. = 2, приведенное выше уравнение сводится к классическому уравнению конвекции-диффузии. Дробное уравнению конвекции-диффузии недавно рассматривался рядом авторов. Он представлен как полезный подход для описания динамики переноса в сложных системах, которые регулируются паттернами аномальной диффузии и не экспоненциальной релаксации [4, 5]. В дробных уравнениях конвекции-диффузии также используется в гидрологических исследованиях подземных вод для моделирования переноса пассивных трассеров, переносимых потоком жидкости в пористой среде [7]. Хотя аналитические подходы, такие как метод преобразования Фурье, методы преобразования Лапласа и метод преобразования Меллина, были предложены для поиска решений в замкнутой форме [1, 6, 8], существует очень мало ФДУ, аналитические решения которых в замкнутой форме доступны. Поэтому исследования по численной аппроксимации и методам решения ФДУ вызывают большой интерес. Разработаны наиболее ранние численные методы для обработки пространственного дробного уравнения конвекции-диффузии или временного дробного уравнения конвекции-диффузии (УКД). Для пространственной дробной УКД многие исследователи использовали обычную дискретизацию Грюнвальда со сдвигом [9] и неявную дискретизацию Эйлера (или Кранка-Николсона) по временным шагам для двусторонних дробных производных Римана-Лиувилля и производной по времени первого порядка соответственно. Затем они построили множество численных обработок пространственной дробной УКД, подробности см. в [9–18] и приведенных там ссылках. Позже, Chen и Deng объединили дискретизацию второго порядка с временной дискретизацией Crank-Nicolson для получения нового численных методов, которые сохраняют второй порядок точности как по времени, так и по пространству для дробной УКД [19, 20]. Даже Chen, Deng, Qu и др. отдельно разработали быстрые вычислительные методы, которые также могут уменьшить требуемую алгоритмическую память для реализации вышеупомянутого численного метода второго порядка; подробности см. в [20, 21]. Кроме того, существуют также некоторые другие интересные численные методы для пространственно-фракционного УКД, см., например, [22–26] для обсуждения этих вопросов. С другой стороны, для дробной по времени УКД многие ранние неявные численные методы были получены путем комбинации приближенной формулы L1 [27] для дробной производной Капуто и пространственной дискретизации первого / второго порядка. Эти численные методы безусловно сходятся с точностью O ( 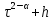 ) или O ( ) или O (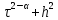 ), где ), где 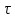 и и 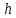 - размер временного шага и размер пространственной сетки соответственно. Чтобы повысить пространственную точность, Cui [28,29] и Mohebbi и Abbaszadeh [30] предложили, соответственно, два компактных экспоненциальных метода и компактный метод конечных разностей для уравнения дробной конвекции-субдиффузии по времени, так что пространственная точность повышается до четвертого порядка. Однако методы и анализ в [28, 30] предназначены только для уравнений с постоянными коэффициентами. В частности, обсуждения в [30] ограничиваются специальным уравнением дробной конвекции-субдиффузии по времени, в котором коэффициенты диффузии и конвекции считаются равными единице. Кроме того, уже были предложены некоторые другие связанные численные методы для обработки дробного УДК по времени, см., например, [31–36]. - размер временного шага и размер пространственной сетки соответственно. Чтобы повысить пространственную точность, Cui [28,29] и Mohebbi и Abbaszadeh [30] предложили, соответственно, два компактных экспоненциальных метода и компактный метод конечных разностей для уравнения дробной конвекции-субдиффузии по времени, так что пространственная точность повышается до четвертого порядка. Однако методы и анализ в [28, 30] предназначены только для уравнений с постоянными коэффициентами. В частности, обсуждения в [30] ограничиваются специальным уравнением дробной конвекции-субдиффузии по времени, в котором коэффициенты диффузии и конвекции считаются равными единице. Кроме того, уже были предложены некоторые другие связанные численные методы для обработки дробного УДК по времени, см., например, [31–36]. Напротив, хотя численные методы для пространственной (или временной) дробной CDE широко исследовались в прошлых исследованиях, работы по численной обработке пространственно-временных дробных уравнений конвекции-диффузии (ПВДУКД) не так уж и много. Во-первых, Zhang [37, 38], Shao и Ma [39], Qin и Zhang [40], и Liu и др. [17] разработали серию исследований о построении неявной разностной схемы (НРС) для ПВДУКД, однако все эти численные схемы могут архивировать сходимость с точностью первого порядка как в пространстве, так и во времени как с теоретической, так и с численной точки зрения. Более того, Liu и др. [17, 41], Zhao и др. [42] и Шэнь [43] рассмотрели возможность решения более общей формы ПВДУКД, в которой пространство первого порядка производная заменяется двусторонней дробной производной Римана-Лиувилля порядка ν ∈ (0, 1). Опять же, их численные методы не могут обладать сходимостью со вторым порядком точности как по пространству, так и по времени. Кроме того, разработаны некоторые другие эффективные подходы для численного решения ПВДУКД. Более того, большинство этих численных методов не имеют полного теоретического анализа как сходимости, так и устойчивости; например, см. подробности в [24, 44–50]. Традиционные методы решения FDE имеют тенденцию генерировать полные матрицы коэффициентов, что требует затрат на вычисления O ( 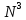 ) и хранения O ( ) и хранения O (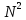 ), где ), где 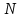 - количество узлов сетки [14,21]. Чтобы оптимизировать вычислительную сложность, Meerschaet и Tadjeran [9] предложили схему дискретизации Грюнвальда со сдвигом со свойством безусловной устойчивости для аппроксимации пространственной дробной УДК. Позже Wang и Wang [14] обнаружили, что линейная система, порожденная этой дискретизацией, имеет специальную Теплицевую матрицу коэффициентов, или, точнее, эту матрицу коэффициентов можно выразить как сумму диагонально-умноженных на Теплицев матриц. Это означает, что требования к хранилищу равно O ( - количество узлов сетки [14,21]. Чтобы оптимизировать вычислительную сложность, Meerschaet и Tadjeran [9] предложили схему дискретизации Грюнвальда со сдвигом со свойством безусловной устойчивости для аппроксимации пространственной дробной УДК. Позже Wang и Wang [14] обнаружили, что линейная система, порожденная этой дискретизацией, имеет специальную Теплицевую матрицу коэффициентов, или, точнее, эту матрицу коэффициентов можно выразить как сумму диагонально-умноженных на Теплицев матриц. Это означает, что требования к хранилищу равно O (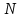 ) вместо O ( ) вместо O (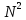 ), а сложность умножения матрицы на вектор требует только O( ), а сложность умножения матрицы на вектор требует только O(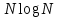 ) операций с помощью быстрого преобразования Фурье (БПФ) [51]. Используя это преимущество, Wang и Wang предложили метод CGNR, имеющий вычислительные затраты O( ) операций с помощью быстрого преобразования Фурье (БПФ) [51]. Используя это преимущество, Wang и Wang предложили метод CGNR, имеющий вычислительные затраты O(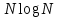 ) для решения линейной системы, и численные эксперименты показывают, что метод CGNR является быстрым, когда коэффициенты диффузии очень малы, т. е. дискретные системы хорошо кондиционированы [14]. Однако дискретные системы становятся плохо обусловленными, когда коэффициенты диффузии не малы. В этом случае метод CGNR сходится медленно. Чтобы исправить этот недостаток, Zhao и др. расширили технику предварительного кондиционирования, которую представили Lin и др. в контексте пространственного уравнения дробной диффузии [52], для работы с линейными системами типа Теплица, полученными в результате численной дискретизации ПВДУКД [42]. Их результаты касались многообещающего ускорения сходимости итерационных методов при решении (1.1). ) для решения линейной системы, и численные эксперименты показывают, что метод CGNR является быстрым, когда коэффициенты диффузии очень малы, т. е. дискретные системы хорошо кондиционированы [14]. Однако дискретные системы становятся плохо обусловленными, когда коэффициенты диффузии не малы. В этом случае метод CGNR сходится медленно. Чтобы исправить этот недостаток, Zhao и др. расширили технику предварительного кондиционирования, которую представили Lin и др. в контексте пространственного уравнения дробной диффузии [52], для работы с линейными системами типа Теплица, полученными в результате численной дискретизации ПВДУКД [42]. Их результаты касались многообещающего ускорения сходимости итерационных методов при решении (1.1).В этой статье мы сначала получаем неявную разностную схему для решения уравнения (1), а затем проверить, что предложенная схема может архивировать устойчивость и сходимость с вторым порядком точностью в пространстве и вовремя (т.е. O ( 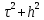 )) от теоретического и числовые перспективы. Насколько нам известно, схема является первой (без техники экстраполяции), которая может иметь сходимость с O ( )) от теоретического и числовые перспективы. Насколько нам известно, схема является первой (без техники экстраполяции), которая может иметь сходимость с O ( Для временного перехода схемы необходимо решить множество линейных систем, которые обладают различными матрицами коэффициентов Теплица. Эти линейные системы могут быть эффективно решены одна за другой с помощью метода подпространств Крылова с подходящими циркулянтными предобуславливателями [51,53], что может значительно снизить вычислительные затраты и память. Специально для ПВДУКД с постоянными коэффициентами мы переходим к представлению обратной матрицы коэффициентов Теплица в виде суммы произведений треугольных матриц Теплица [51,54], так что решение каждой линейной системы для движения во времени может быть получено непосредственно через несколько быстрые преобразования Фурье (БПФ). Чтобы получить явное представление обращения матриц Теплица, необходимо решить только две конкретные линейные системы с одной и той же матрицей коэффициентов Теплица, что может быть выполнено с помощью методов предварительно обусловленных подпространств Крылова [55] со сложностью O ( Для временного перехода схемы необходимо решить множество линейных систем, которые обладают различными матрицами коэффициентов Теплица. Эти линейные системы могут быть эффективно решены одна за другой с помощью метода подпространств Крылова с подходящими циркулянтными предобуславливателями [51,53], что может значительно снизить вычислительные затраты и память. Специально для ПВДУКД с постоянными коэффициентами мы переходим к представлению обратной матрицы коэффициентов Теплица в виде суммы произведений треугольных матриц Теплица [51,54], так что решение каждой линейной системы для движения во времени может быть получено непосредственно через несколько быстрые преобразования Фурье (БПФ). Чтобы получить явное представление обращения матриц Теплица, необходимо решить только две конкретные линейные системы с одной и той же матрицей коэффициентов Теплица, что может быть выполнено с помощью методов предварительно обусловленных подпространств Крылова [55] со сложностью O ( ). Краткое содержание этой статьи выглядит следующим образом. Во втором разделе мы устанавливаем неявную разностную схему для (1.1) и доказываем, что эта схема безусловно устойчива и сходится с точностью порядка O ( ). Краткое содержание этой статьи выглядит следующим образом. Во втором разделе мы устанавливаем неявную разностную схему для (1.1) и доказываем, что эта схема безусловно устойчива и сходится с точностью порядка O ( ). В третьем разделе мы исследуем, что полученные линейные системы имеют несимметричные Теплицевые матрицы, а затем разрабатываем методы быстрого решения, основанные на методах предварительно обусловленных подпространств Крылова, для решения (1), используя свойство матрицы Теплица неявной разностной схемы. Наконец, мы представляем численные эксперименты, чтобы проиллюстрировать эффективность наших численных подходов в четвертом разделе и дайте заключительные замечания в разделе пять. ). В третьем разделе мы исследуем, что полученные линейные системы имеют несимметричные Теплицевые матрицы, а затем разрабатываем методы быстрого решения, основанные на методах предварительно обусловленных подпространств Крылова, для решения (1), используя свойство матрицы Теплица неявной разностной схемы. Наконец, мы представляем численные эксперименты, чтобы проиллюстрировать эффективность наших численных подходов в четвертом разделе и дайте заключительные замечания в разделе пять. |
