Практическая работа по предмету статистика с основами эконометрики с 13 по 33 задачи. Практическая работа_Зимин_22-МБ568. Отчет по самостоятельной работе по предмету Статистика
 Скачать 270.27 Kb. Скачать 270.27 Kb.
|
|
Образовательная организация высшего образования (Частное учреждение) «Международная Академия Бизнеса и Новых Технологий» (МУБиНТ) Кафедра_Менеджмент_ Специальность_Интернет-маркетинг и управление маркетинговой деятельностью ОТЧЕТ По самостоятельной работе по предмету Статистика Выполнил студент 1 курса Группы № 22-МБ568 Зимин Дмитрий Николаевич Руководитель лабораторной работы Гультяев Вячеслав Евгеньевич Отчет защищен с оценкой ___ Ярославль, 2022 Задание 1 – Решение примеров по образцу Пример 13 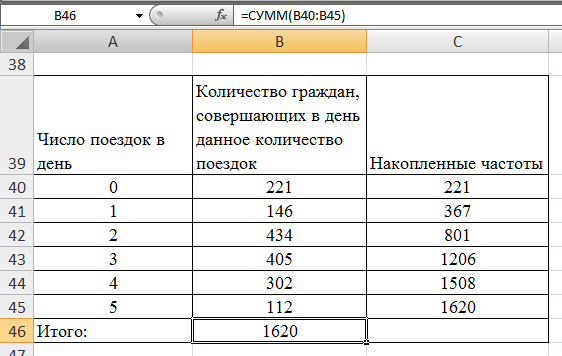 Рисунок 1 Для представленного ряда наиболее часто встречающимся вариантом является 2 поездки в день, то есть мода равна 2. При четном числе элементов вариационного ряда за медиану принимают среднюю арифметическую из двух центральных вариант упорядоченного ряда. Так по данным, представленным на Рисунке из 1620 элементов (общей сумме поездок) 810 и 811 будут являться центральными: они оба равны 3. Расчет медианы проведен следующим образом: (3+3)/2 = 3, то есть медиана равна 3. Пример 14 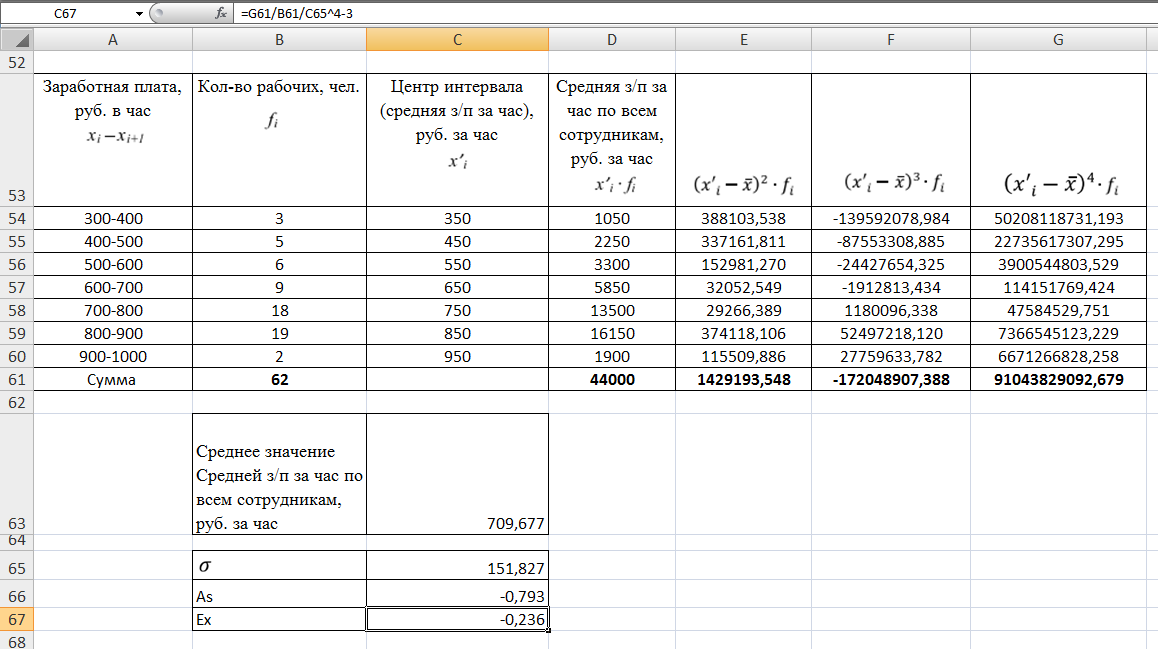 Рисунок 2 Данные представлены в виде интервального ряда (шаг 100 руб.). Для определения показателей ассиметрии и крутизны необходимо найти среднее и среднее квадратическое отклонение распределения. Среднее значение вычислим по формуле средней арифметической взвешенной, для этого необходимо найти отношение средней заработной платы за час по всем сотрудникам к числу сотрудников. хср=44000/62=709,677 руб. за час. (средний уровень заработной платы 62 сотрудников за час составляет 709,68 руб.). Далее найдем среднее квардратическое отклонение ( 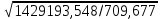 =151,827. =151,827.Коэффициент ассиметрии рассчитан следующим образом: As = 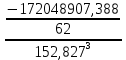 = -0,793 = -0,793В данном случае As меньше 0, то есть в вариационном ряду преобладают варианты, которые меньше средней (хср) и распределение имеет более длинную ветвь слева (скошено влево): левостороннее ассиметричное распределение. Далее найдем эксцесс распределения: Ex = 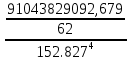 = -0,236 = -0,236В примере показатель Ex меньше 0, значит крутизна распределения плосковершинная. Пример 15 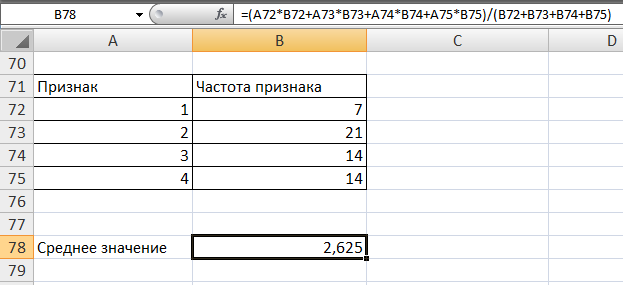 Рисунок 3 В представленных данных чаще всего встречается значение признака 2 (его частота 21 является максимальной из всех представленных в задаче). Так, Мода = 2. Среднее значение (xср) рассчитано по формуле средней взвешенной (рисунок 3). Таким образом, хср = 2,625 > Мо = 2, таким образом, в данном случае мы имеем правостороннюю асимметрию, то есть показатель As>0 (Рисунок 4).  Рисунок 4 Пример 16 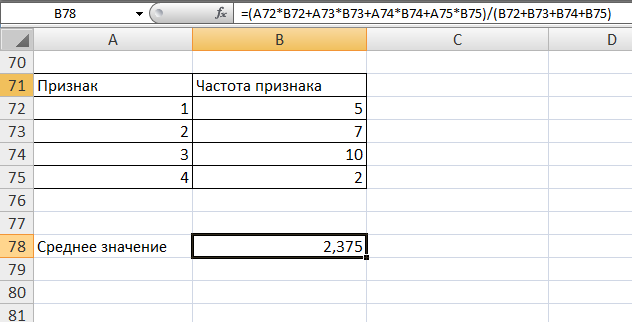 Рисунок 5 В представленных данных чаще всего встречается значение признака 3 (его частота 10 является максимальной из всех представленных в задаче). Так, Мода = 3. Среднее значение (xср) рассчитано по формуле средней взвешенной (рисунок 5). Таким образом, хср = 2,375 < Мо = 3, таким образом, в данном случае мы имеем левостороннюю асимметрию, то есть показатель As<0 (Рисунок 6). 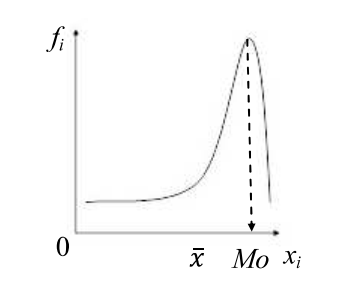 Рисунок 6 Пример 17 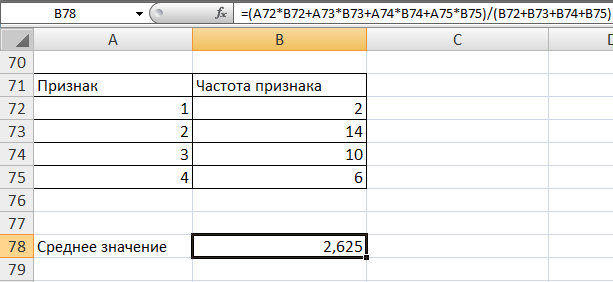 Рисунок 7 В представленных данных чаще всего встречается значение признака 2 (его частота 14 является максимальной из всех представленных в задаче). Так, Мода = 2. Среднее значение (xср) рассчитано по формуле средней взвешенной (рисунок 7). Таким образом, хср = 2,625 > Мо = 2, таким образом, в данном случае мы имеем правостороннюю асимметрию, то есть показатель As>0 (Рисунок 8). 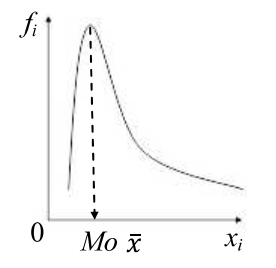 Рисунок 8 Пример 18 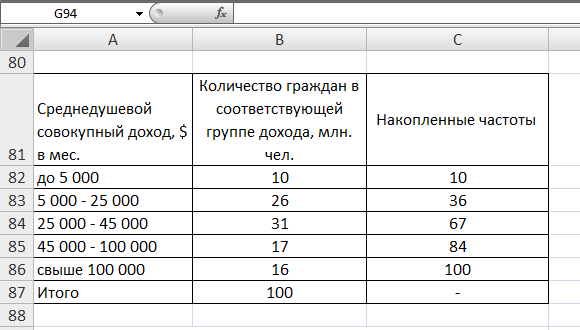 Рисунок 9 В задаче требуется найти децильный коэффициент дифференциации. Население упорядочено по среднедушевому совокупному доходу (по возрастанию, рисунок 9). В совокупности население составляет 100 млн. чел. (100%). Необходимо рассчитать первый и девятый дециль. Возьмем первую 1/10 часть наименее обеспеченного населения (от 0% до 10%: здесь максимальная граница интервала 10%, поэтому гражданин соответствующий 10% будет иметь максимальный доход из этой группы. Первый дециль = Д1= 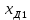 + +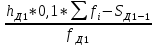 Для нахождения интервала, содержащего первый дециль воспользуемся накопленными частотами, 10% попадает в первый интервал, так как 10% населения получает доход до 5 000 $ в мес. Ширина данного интервала определяется по ближайшему к нему интервалу 5 000 - 25 000 $ в мес. Ширина = 20 000 $ в мес. и интервал имел бы вид -15 000 – 5 000 $ в мес., но так как доход не может быть отрицательным, интервал принимает вид 0 – 5000 $ в мес. Ширина интервала равна 5 000 $ в мес. ( 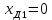 , , 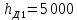 ). Частота в первом дециальном интервале равна ). Частота в первом дециальном интервале равна 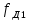 = 10, накопленная частота в предыдущем децильном интервале = 10, накопленная частота в предыдущем децильном интервале 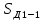 = 0. = 0. Д1 = 0 + 5 000 * (0,1*100-0)/10 = 5 000 $ в мес., то есть максимальный доход 10% наименее обеспеченного населения составляет 5 000 $ в мес. Далее произведем расчет минимального дохода 10% наиболее обеспеченного населения (девятый дециль). 90%-й децильный интервал – это интервал с доходом более 100 000 $ в мес. (84-100% населения получает доход в размере более 101 000 $ в мес.). Ширина данного интервала определяется по ближайшему к нему интервалу 45 000 - 100 000 $ в мес. Ширина = 55 000 $ в мес., интервал принимает вид 100 000 – 155 000 $ в мес. ( 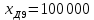 , , 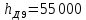 ). Частота в девятом дециальном интервале равна ). Частота в девятом дециальном интервале равна 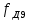 = 16, накопленная частота в предыдущем децильном интервале = 16, накопленная частота в предыдущем децильном интервале 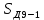 = 84. = 84.Д9 = 100 000 + 55 000*(0,9*100-84)/16 = 120 625 $ в мес., то есть минимальный доход 10% наиболее обеспеченного населения составляет 120 625 $ в мес. Децильный коэффициент дифференциации рассчитан по формуле: Кд = Д9/Д1 = 120 625 / 5000 = 24,125 Таким образом, минимальные доходы 10% наиболее обеспеченных граждан превышают в 12,125 раз максимальные доходы 10% наименее обеспеченного уровня населения. Пример 19 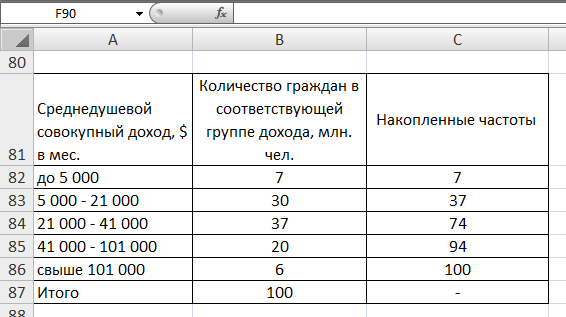 Рисунок 10 В задаче требуется найти децильный коэффициент дифференциации. Население упорядочено по среднедушевому совокупному доходу (по возрастанию, рисунок 10). В совокупности население составляет 100 млн. чел. (100%). Необходимо рассчитать первый и девятый дециль. Возьмем первую 1/10 часть наименее обеспеченного населения (от 0% до 10%: здесь максимальная граница интервала 10%, поэтому гражданин соответствующий 10% будет иметь максимальный доход из этой группы. Первый дециль = Д1= 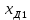 + +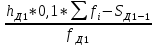 Для нахождения интервала, содержащего первый дециль воспользуемся накопленными частотами, 10% попадает во второй интервал, так как 37% населения получает доход до 21 000 $ в мес. Ширина данного интервала 5 000 - 21 000 $ в мес. Ширина = 16 000 $ в мес. ( 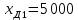 , , 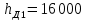 ). Частота в первом дециальном интервале равна ). Частота в первом дециальном интервале равна 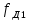 = 30, накопленная частота в предыдущем децильном интервале = 30, накопленная частота в предыдущем децильном интервале 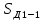 = 7. = 7. Д1 = 5 000 + 16 000 * (0,1*100-7)/30 = 6600 $ в мес., то есть максимальный доход 10% наименее обеспеченного населения составляет 6600 $ в мес. Далее произведем расчет минимального дохода 10% наиболее обеспеченного населения (девятый дециль). 90%-й децильный интервал – это интервал с доходом 41 000 - 101 000 $ в мес. (74-94% населения получает доход в размере от 41 000 до 101 000 $ в мес.). Ширина данного интервала 60 000 $ в мес. ( 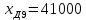 , , 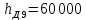 ). Частота в девятом дециальном интервале равна ). Частота в девятом дециальном интервале равна 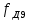 = 20, накопленная частота в предыдущем децильном интервале = 20, накопленная частота в предыдущем децильном интервале 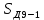 = 74. = 74.Д9 = 41 000 + 60 000*(0,9*100-74)/20 = 89 000 $ в мес., то есть минимальный доход 10% наиболее обеспеченного населения составляет 89 000 $ в мес. Децильный коэффициент дифференциации рассчитан по формуле: Кд = Д9/Д1 = 89 000 / 6600 = 13,485 Таким образом, минимальные доходы 10% наиболее обеспеченных граждан превышают в 13,485 раз максимальные доходы 10% наименее обеспеченного уровня населения. Пример 20 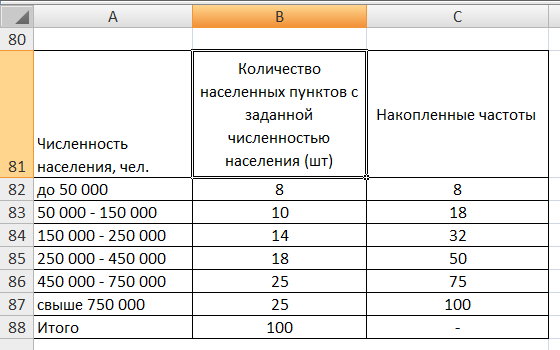 Рисунок 11 По данным задачи необходимо найти квантильный коэффициент дифференциации. Все населенные пункты упорядочены по численности (по возрастанию, рисунок 11). Всего в выборке 100 населенных пунктов, которые составляют 100%. Для вычисления квантильного коэффициента необходимо найти первый (20%) и четвертый (80%) квантили. Первый квантиль рассчитывается по формуле: Первый квантиль = К1 = 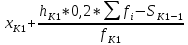 Первый квантиль показывает максимальную численность населения в 1/20 части (0-20%) самых малочисленных городов страны. Для нахождения интервала, содержащего первый квантиль, используются накопленные частоты. В данном случае, первый квантиль содержится в третьем интервале (18-32% населенных пунктов имеет численность 150 000 – 250 000 чел.). Ширина данного интервала ( 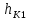 ) 100 000 чел., нижняя граница ( ) 100 000 чел., нижняя граница (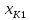 ) 150 000 чел., частота в первом квантильном интервале ( ) 150 000 чел., частота в первом квантильном интервале (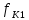 ) 14, накопленная частота в предшствующем интервале составила 18 ( ) 14, накопленная частота в предшствующем интервале составила 18 (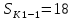 ). Так, первый квантиль равен: ). Так, первый квантиль равен:К1 = 150 000 + 100 000 * (0,2*100-18)/14 = 164 285 чел. Так, максимальная численность населения 20% наименее населенных городов составляет 164 285 чел. Четвертый квантиль (80%) показывает минимальную численность населения в (80-100%) самых крупнонаселенных городах. Четвертый квантиль = К4 = 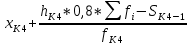 Для нахождения интервала, содержащего четвертый квантиль, используются накопленные частоты. В данном случае, четвертый квантиль содержится в шестом интервале (75-100% населенных пунктов имеет численность более 750 000 чел.). Ширина данного интервала определяется по ближайшему к нему интервалу 450 000 – 750 000 чел., ширина ( 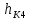 ) = 300 000 чел. и интервал принимает вид 750 000 – 1 050 000 чел., нижняя граница ( ) = 300 000 чел. и интервал принимает вид 750 000 – 1 050 000 чел., нижняя граница (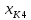 ) 750 000, частота в четвертом квантильном интервале ( ) 750 000, частота в четвертом квантильном интервале (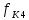 ) 25, накопленная частота в предшествующем интервале 75 ( ) 25, накопленная частота в предшествующем интервале 75 (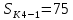 ). Так, четвертый квантиль равен: ). Так, четвертый квантиль равен:К4 = 750 000 + 300 000 * (0,8*100-75)/25 = 810 000 чел. Так, минимальная численность населения 20% самых густонаселенных городов составляет 810 000 чел. Квантильный коэффициент рассчитан следующим образом: Кк = К4/К1 = 810 000 / 164 285 = 4,9305 Таким образом, минимальная численность населения 20% наиболее крупнонаселенных городов в 4,9305 раз превышает максимальную численность населения 20% самых малонаселенных городов. Пример 21 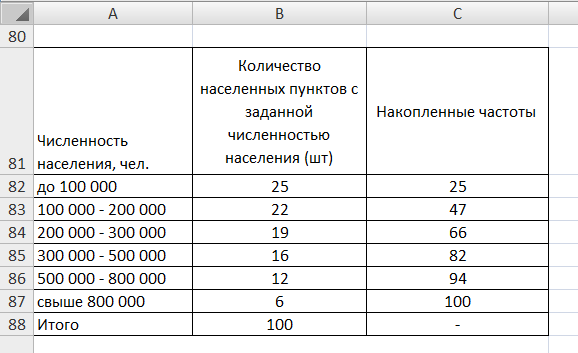 Рисунок 12 По данным задачи необходимо найти квантильный коэффициент дифференциации. Все населенные пункты упорядочены по численности (по возрастанию, рисунок 12). Всего в выборке 100 населенных пунктов, которые составляют 100%. Для вычисления квантильного коэффициента необходимо найти первый (20%) и четвертый (80%) квантили. Первый квантиль рассчитывается по формуле: Первый квантиль = К1 = 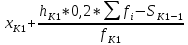 Первый квантиль показывает максимальную численность населения в 1/20 части (0-20%) самых малочисленных городов страны. Для нахождения интервала, содержащего первый квантиль, используются накопленные частоты. В данном случае, первый квантиль содержится в первом интервале (0-25% населенных пунктов имеет численность до 100 000 чел.). Ширина данного интервала ( 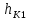 ) 100 000 чел., нижняя граница ( ) 100 000 чел., нижняя граница (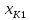 ) 0, частота в первом квантильном интервале ( ) 0, частота в первом квантильном интервале (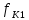 ) 25, накопленная частота в предшствующем интервале отсутствует ( ) 25, накопленная частота в предшствующем интервале отсутствует (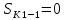 ). Так, первый квантиль равен: ). Так, первый квантиль равен:К1 = 0 + 100 000 * (0,2*100-0)/25 = 80 000 чел. Так, максимальная численность населения 20% наименее населенных городов составляет 80 000 чел. Четвертый квантиль (80%) показывает минимальную численность населения в (80-100%) самых крупнонаселенных городах. Четвертый квантиль = К4 = 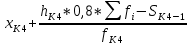 Для нахождения интервала, содержащего четвертый квантиль, используются накопленные частоты. В данном случае, четвертый квантиль содержится в четвертом интервале (66-82% населенных пунктов имеет численность 300 000 – 500 0000 чел.). Ширина данного интервала ( 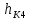 ) 200 000 чел., нижняя граница ( ) 200 000 чел., нижняя граница (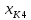 ) 300 000, частота в четвертом квантильном интервале ( ) 300 000, частота в четвертом квантильном интервале (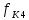 ) 16, накопленная частота в предшествующем интервале 66 ( ) 16, накопленная частота в предшествующем интервале 66 (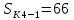 ). Так, четвертый квантиль равен: ). Так, четвертый квантиль равен:К4 = 300 000 + 200 000 * (0,8*100-66)/16 = 475 000 чел. Так, минимальная численность населения 20% самых густонаселенных городов составляет 475 000 чел. Квантильный коэффициент рассчитан следующим образом: Кк = К4/К1 = 475 000 / 80 000 = 5,9375 Таким образом, минимальная численность населения 20% наиболее крупнонаселенных городов в 5,9375 раз превышает максимальную численность населения 20% самых малонаселенных городов. |
