Практическая работа № 11. Отчет попрактическойработе8 построение комбинационных схем, реализующих сднф и скнф

• Название: Отчет попрактическойработе8 построение комбинационных схем, реализующих сднф и скнф
• Дата: 26.12.2021
• Размер: 0.69 Mb.
• Имя файла: Практическая работа № 11.docx
• Тип: Отчет; #318647

МИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ

Федеральное государственное бюджетное образовательное учреждение

высшего образования

"МИРЭА - Российский технологический университет"

РТУ МИРЭА

Институт искусственного интеллекта

Кафедра общей информатики (ОИ)


ОТЧЕТ

ПОПРАКТИЧЕСКОЙРАБОТЕ№ 8

построение комбинационных схем, реализующих СДНФ и СКНФ

заданной логической функции от 4-х переменных

по дисциплине

«ИНФОРМАТИКА»


Выполнил студент группы ИКБО-35-21 Махин.Г.С.
Принял Ассистент ОИ Тябут .Е.А.

Практическая	«__»_______2021 г.	_______________
работа выполнена
«Зачтено»	«__»_______2021 г.	_______________

Москва 2021

СОДЕРЖАНИЕ

РТУ МИРЭА 1

1.Постановка задачи 2

2.Восстановленная таблица истинности 3

3.Проектирование оптимальных схем управления триггерами 4

4.Реализация счетчика с оптимальной схемой управления 13

5.Реализация счетчика на преобразователе кодов 14

6.Выводы 15

7.Список информационных источников 16

1.Постановка задачи

Разработать счетчик с параллельным переносом на D-триггерах двумя способами:

с оптимальной схемой управления, выполненной на логических элементах общего базиса;

со схемой управления, реализованной на преобразователе кодов (быстрая реализация, но не оптимальная схема).

В качестве исходных данных использовать индикатор CNT лабораторного комплекса, на котором слева направо отображены:

направление счета (0 —сложение, 1 —вычитание);

максимальное значение счетчика (не путать с модулем счета);

шаг счета.

Протестировать работу схемы и убедиться в ее правильности.

2.Восстановленная таблица истинности

Имеются следующие исходные данные:

направление счета - сложение;

максимальное значение счетчика – D;

шаг счета - 9.

По исходным данным восстановим таблицу переходов счетчика (таблица 1).
Таблица 1. Таблица переходов счётчика

Q3(t)	Q2(t)	Q1(t)	Q0(t)	Q3(t+1)	Q2(t+1)	Q1(t+1)	Q0(t+1)
0	0	0	0	1	0	0	1
0	0	0	1	1	0	1	0
0	0	1	0	1	0	1	1
0	0	1	1	1	1	0	0
0	1	0	0	1	1	0	1
0	1	0	1	0	0	0	0
0	1	1	0	0	0	0	1
0	1	1	1	0	0	1	0
1	0	0	0	0	0	1	1
1	0	0	1	0	1	0	0
1	0	1	0	0	1	0	1
1	0	1	1	0	1	1	0
1	1	0	0	0	1	1	1
1	1	0	1	1	0	0	0
1	1	1	0	*	*	*	*
1	1	1	1	*	*	*	*

3.Проектирование оптимальных схем управления триггерами

Таблица переходов является частично определенной: состояния 1110 и 1111 согласно исходным данным возникать никогда не должны, поэтому очередное состояние Q(t+1) для этих случаев мы можем интерпретировать как нам удобно в целях минимизации управляющей логики. Рассматриваем столбцы Q_i(t+1) как самостоятельные функции от четырех переменных и проводим их минимизацию. Также нам необходимо для каждой функции из двух возможных минимальных форм выбрать самую короткую. Допустим, начнем с функции Q₃(t+1). Оценим сложность минимальных форм, которые для нее получатся, по количеству переменных, входящих в них, и выберем оптимальную форму. Для этого построим необходимые карты Карно.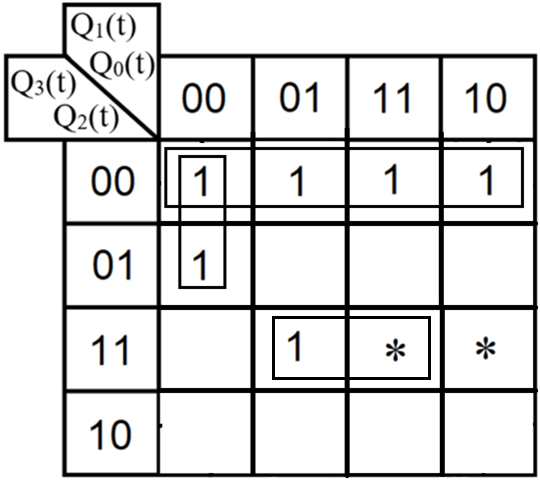



Рисунок 1 – Карта Карно для МДНФ функции Q₃(t+1)

Пока не будем записывать формулу МДНФ, но оценим ее сложность. Это

легко сделать, поскольку известно количество переменных, необходимых для

описания каждого из интервалов. Напомним это количество для случая логической функции от четырех переменных:

– интервал размера 1 описывается четырьмя переменными;

– интервал размера 2 описывается тремя переменными;

– интервал размера 4 описывается двумя переменными;

– интервал размера 8 описывается одной переменной.

Из рисунка 1 видно, что в нашем случае МДНФ Q3(t+1) будет описана при помощи 2 + 3 + 3 = 8 переменных либо их отрицаний.

Теперь проделаем аналогичную операцию для МКНФ этой же функции. Возьмем за основу уже построенную карту на рис. 46, ведь на всех пустых клетках там стоят нули. Кроме того, для повышения наглядности удалим единичные значения. Попытаемся интерпретировать звездочки как нулевые значения функции. Выделим интервалы, получится следующий рис. 2.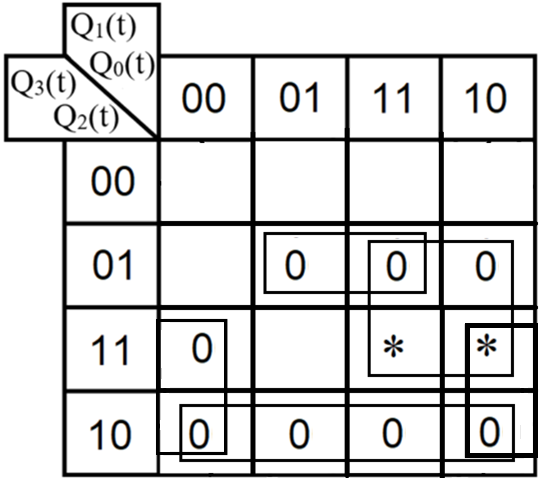


Рисунок 2 - Карта Карно для МКНФ функции Q₃(t+1)

На рис.47 хорошо видно, что понимание звездочек как нулей не улучшает существующие интервалы, но приводит к ненужному усложнению: появляется лишний интервал размера четыре. Поэтому в данном случае звездочки следует интерпретировать как единичные значения. Итого имеем: один интервал размера четыре и три интервала размера три. Значит МКНФ будет иметь 3 * 3 + 2 + 2 = 13 переменных либо их отрицаний, что эквивалентно сложности МДНФ. Делаем вывод, что МДНФ функции Q₃(t+1) строить выгоднее, чем МКНФ.

Запишем формулу для МДНФ функции Q₃(t+1) (формула 1):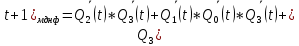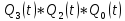





Далее по приведенной методике рассуждений рассмотрим функциюQ2(t+1). Сначала построим карту Карно для МДНФ (рис. 3).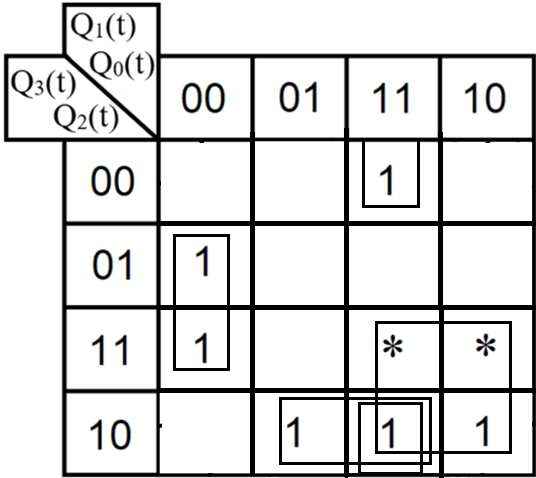



Рис.3 Карта Карно для МДНФ функции Q2(t+1)

Оценим сложность МДНФ: 3 *3 + 2 = 11 переменных или их отрицаний. Теперь построим интервалы из нулевых значений попытаемся интерпретировать звездочки как нули, чтобы построить МКНФ (рис.4).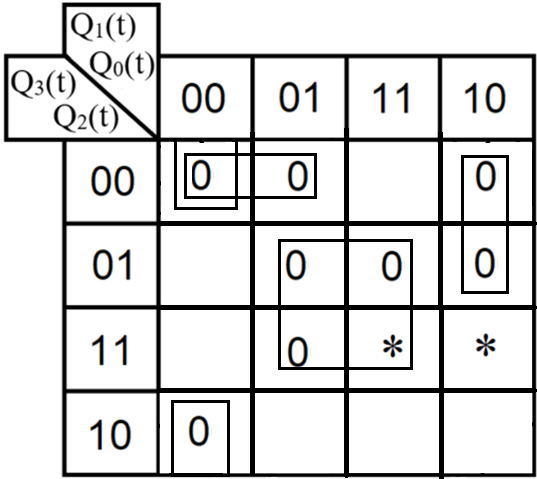



Рис. 4 Карта Карно для МКНФ функции Q2(t+1)

Оценим сложность МКНФ: 3 * 3 + 2 + 2= 13 переменных или их отрицаний. Таким образом получается, что МДНФ для Q₂(t+1) строить выгоднее, чем МКНФ.

Запишем формулу для МДНФ Q₂(t+1) (формула 2):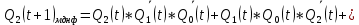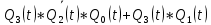





Переходим к рассмотрению Q1(t+1). Построим карту Карно для записи МДНФ этой функции (рис. 5).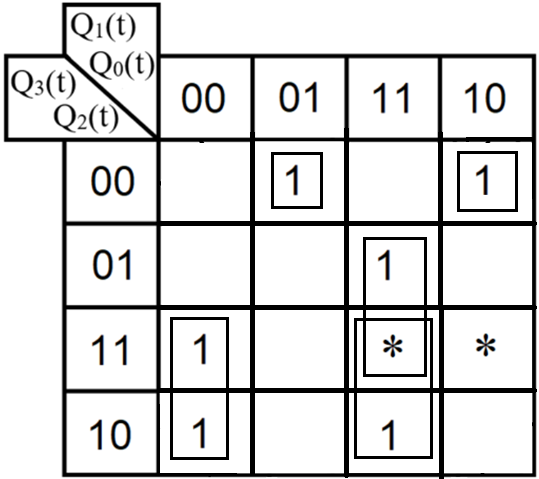



Рис.5 Карта Карно для МДНФ функции Q1(t+1)

Оценим сложность МДНФ: 3 * 4 + 4 = 16 переменных или их отрицаний. Теперь построим интервалы из нулевых значений и попытаемся интерпретировать звездочки как нули, чтобы построить МКНФ (рис.6).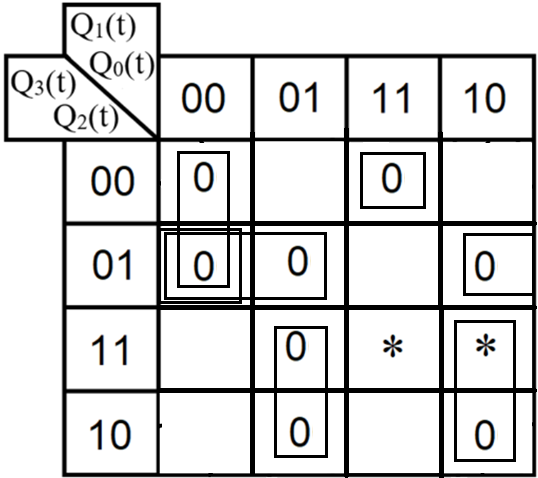



Рис. 6 Карта Карно для МКНФ функции Q1(t+1)

Оценим сложность МКНФ: 5*3 + 4 = 19 переменных или их отрицаний. Таким образом получается, что МДНФ для Q₁(t+1) строить выгоднее, чем МКНФ.

Запишем формулу для МДНФ Q₁ (t+1) (формула 3):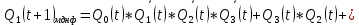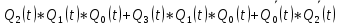





Переходим к рассмотрению Q0(t+1). Построим карту Карно для записи МДНФ этой функции (рис. 7).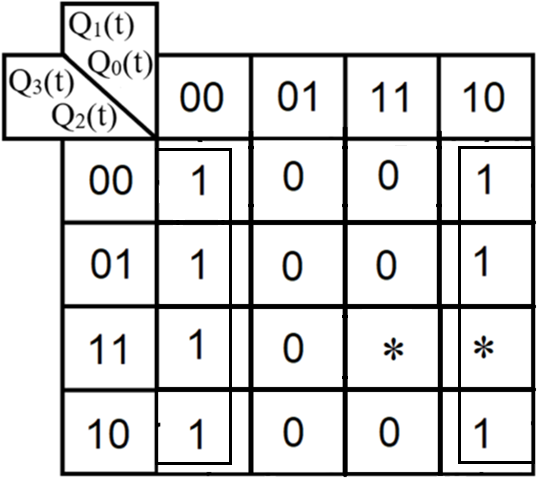



Рис. 7 Карта Карно для МКНФ функции Q0(t+1)

Оценим сложность МДНФ: 2 * 1 = 2 переменных или их отрицаний. Теперь построим интервалы из нулевых значений и попытаемся интерпретировать звездочки как нули, чтобы построить МКНФ (рис.8).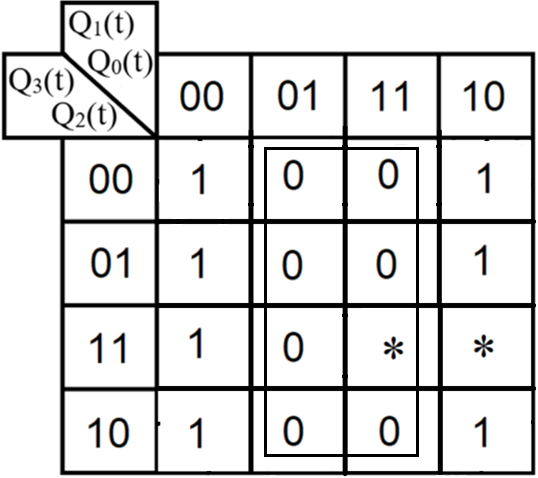



Рис. 8 Карта Карно для МКНФ функции Q0(t+1)

Оценим сложность МКНФ: 2 * 1 = 2 переменных или их отрицаний. Таким образом переменных либо их отрицаний, что эквивалентно сложности МДНФ. Следовательно, нам все равно, какую минимальную форму взять. Запишем формулу для МДНФ Q0 (t+1) (формула 4):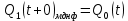

4.Реализация счетчика с оптимальной схемой управления

При помощи полученных формул выполним реализацию схем управления триггеров счетчика (см. рис. 9).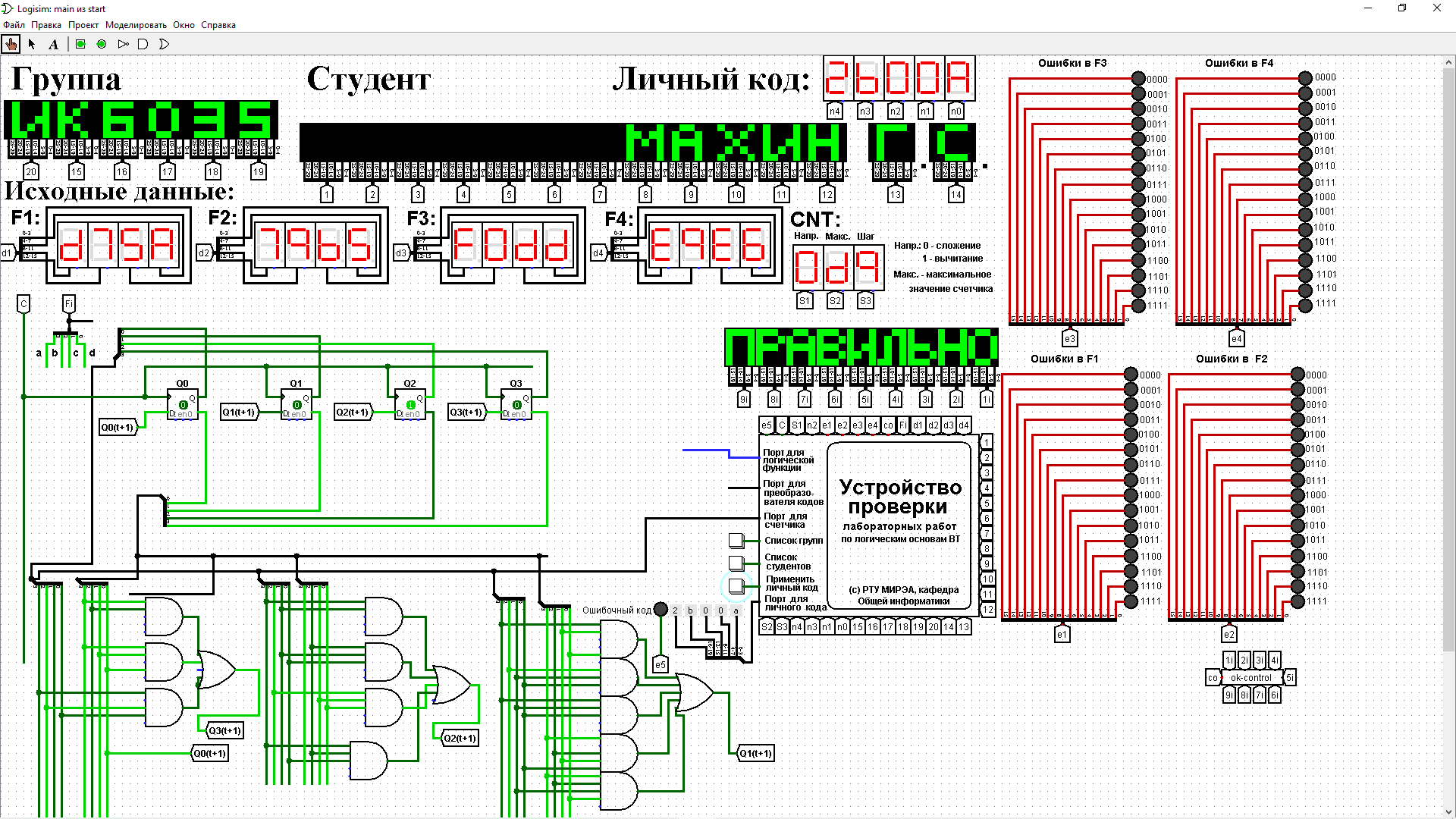



Рисунок 9 - Схема счетчика с подключением к устройству проверки

Тестирование показало правильность работы схемы.

5.Реализация счетчика на преобразователе кодов

Выполним быструю реализацию счетчика при помощи преобразователя кодов в качестве схемы управления триггерами. Здесь не требуется никакая минимизация, необходимо просто по таблице переходов правильно соединить выходы дешифратора со входами шифратора. Таким образом, можно сразу построить схему счетчика (рис.10).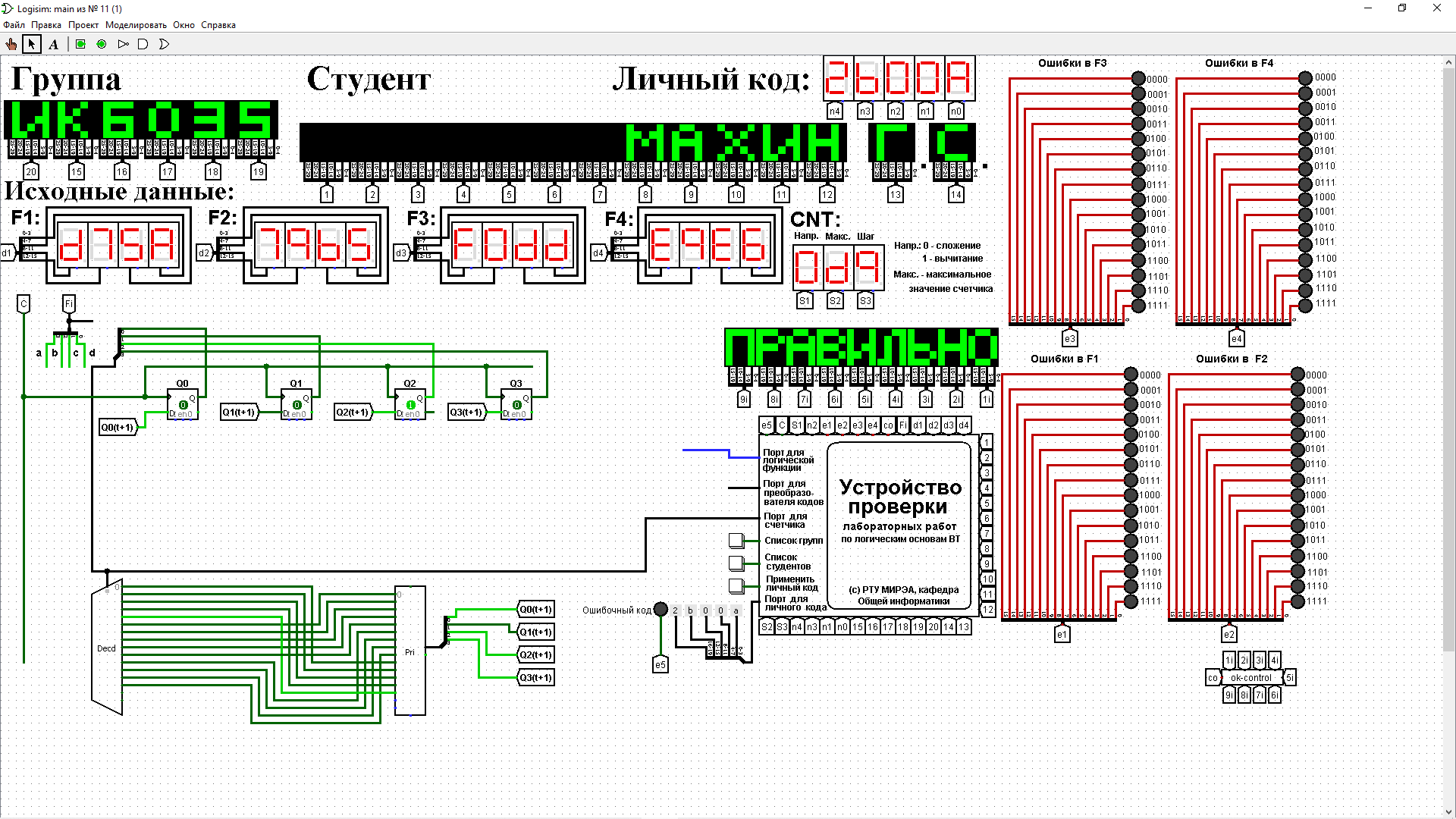


Рисунок 10 – Счетчик со схемой управления, выполненной на преобразователе кодов

Тестирование показало, что схема работает правильно.

6.Выводы

В ходе практической работы был разработан счетчик с параллельным переносом на D-триггерах двумя способами: с оптимальной схемой управления, выполненной на логических элементах общего базиса и со схемой управления, выполненной на преобразователе кодов. Разработанные счётчики были построены в лабораторном комплексе. Тестирование показало правильность работы схем.

7.Список информационных источников

Информатика: Методические указания по выполнению практических работ / С.С. Смирнов, Д.А. Карпов – М., МИРЭА – Российский технологический университет, 2020. –102с.

Лекции. Информатика. Смирнов С. С., МИРЭА – Российский технологический университет, 2021.

Logisim – графический инструмент для разработки и моделирования логических схем [Электронный ресурс] URL: http://www.cburch.com/logisim/ru/ (Последнее обращение 19.11.2021)