Отчет защищен с оценкой О. И. Пята (подпись преподавателя) (инициалы, фамилия)
 Скачать 194.18 Kb. Скачать 194.18 Kb.
|
|
Бийский технологический институт (филиал) федерального государственного бюджетного образовательного учреждения высшего образования «Алтайский государственный технический университет им. И.И. Ползунова» Факультет технологический Кафедра Методов и средств измерений и автоматизации Отчет защищен с оценкой______________ ____________________________О.И. Пята (подпись преподавателя) (инициалы, фамилия) “____”___________ 2022 г. Отчет по лабораторной работе № 2
ЛР 15.03.06.01.000 ОТ (обозначение документа) Студент группы МиР-91 _____________________ Д.А. Теплов (инициалы, фамилия) Преподаватель ____________________ О.И. Пята____ (инициалы, фамилия) БИЙСК 2022 Цель лабораторной работы: изучение методики выполнения прямых измерений с многократными наблюдениями. Получение навыков стандартной обработки результатов наблюдений, оценивания погрешностей и представления результатов измерений. Задачи лабораторной работы: провести определение точечных оценок результатов измерений. Вариант набора исходных данных (приложение А). проверить выборку на наличие грубых и ошибок (промахов), при наличии промаха результат исключить из выборки, с последующим пересчетом среднего значения и СКО. определить закон распределения результатов измерений. Здесь по результатам измерений и проведенным расчетам построить гистограмму. оценить закон распределения по статистическим критериям. определить доверительные границы случайной погрешности. определить границы неисключенной погрешности с учетом того, что результаты измерения напряжения получены с помощью универсального многопредельного цифрового прибора. Для прибора нормировано выражение для определения относительной погрешности: 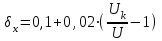 При измерении напряжения могут быть установлены следующие поддиапазоны: от 0,0 мВ до 199,9 мВ; от 0,000 В до 1,999 В; от 0,00 В до 19,99 В; от 0,0 В до 199,9 В; от О В до 1999 В. определить доверительные границы погрешности результата измерения. Ход работы: Проводим определение точечных оценок результатов измерений. Выбираем вариант набора исходных данных (приложение А). Выданный преподавателем вариант-3. Далее набор исходных данных вносим в программу Excel, и сортируем по возрастанию (рисунок 1). 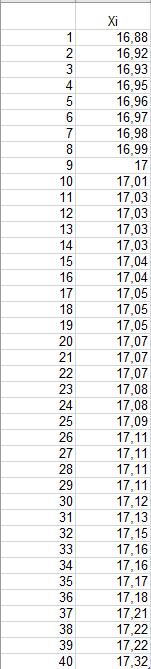 Рисунок 1 – Набор исходный данных Проверим выборку на наличие грубых ошибок (промахов). Определим среднее арифметическое ряда наблюдений (рисунок 2). Рисунок 2 – Среднее арифметическое ряда наблюдений Для определения среднего квадратического отклонения, сперва нужно найти разность между каждым значением в выборке и средне арифметическим ряда рассчитанным ранее. Затем полученные значения возвести в квадрат и посчитать сумму полученного ряда. Формула для определения СКО:  . Полученное значение СКО представлено на рисунке 3. . Полученное значение СКО представлено на рисунке 3.Рисунок 3 – Среднее квадратическое отклонение Проверка наличия промахов в выборке проводится с использованием статистических критериев, такими критериями являются: критерий Романовского, критерий Шарлье, критерий Диксона. Критерий Романовского можно применять, даже если число измерений n < 20. При этом вычисляется отношение 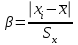 . Обнаружение промахов в выборке по критерию Романовского проводится следующим образом: задаются уровнем значимости q = 0,05 и выбирают табличное значение критерия Романовского исходя из уровня значимости и количества значений в выборке. Табличное значение критерия Романовского выбрали . Обнаружение промахов в выборке по критерию Романовского проводится следующим образом: задаются уровнем значимости q = 0,05 и выбирают табличное значение критерия Романовского исходя из уровня значимости и количества значений в выборке. Табличное значение критерия Романовского выбрали 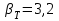 . Далее сравнивают табличное значение с расчетным. Если расчетное значение критерия Романовского оказалось больше табличного значения, тогда результат считается промахом и отбрасывается. . Далее сравнивают табличное значение с расчетным. Если расчетное значение критерия Романовского оказалось больше табличного значения, тогда результат считается промахом и отбрасывается.Следующий критерий Шарлье. Он используется, если число измерений n > 20. Тогда по теореме Бернулли число результатов, отбрасывается результат, для значения которого выполняется неравенство  . Значение критерия Шарлье выбираем из таблицы исходя их количества значений в выборке. . Значение критерия Шарлье выбираем из таблицы исходя их количества значений в выборке.Вариационный критерий Диксона не показывает какой конкретно результат является промахом. Этот критерий только указывает на, то есть ли в выборке промах или промаха нет. Чтобы узнать есть ли в выборке промах по критерию Диксона воспользуемся формулой: 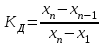 . Далее полученный результат сравнивают с табличным критерием Диксона, если расчетный критерий оказался меньше табличного значит в выборке промахом нет. . Далее полученный результат сравнивают с табличным критерием Диксона, если расчетный критерий оказался меньше табличного значит в выборке промахом нет.Результаты проверки по трем критериям представлены на рисунке 4. По критерию Романовского промахи в выборке не выявили. По критерию Шарлье и критерию Диксона наличие промаха в выборке подтвердилось. 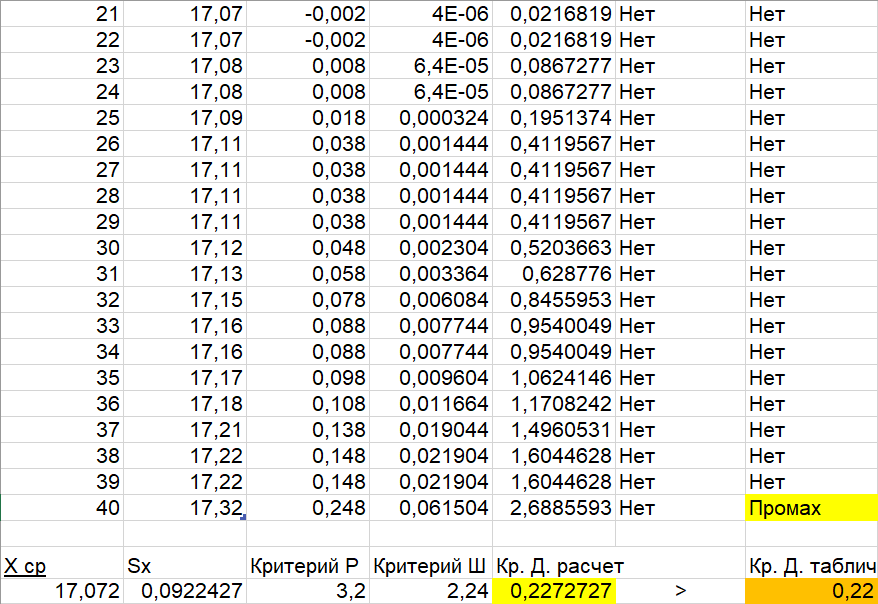 Рисунок 4 – Результат проверки на наличие промахов в выборке Значение, в выборке которое является промахом необходимо исключить для дальнейших расчетов. Далее набор исходных данных выделяем без значения который является промахом и копируем в новую область листа в программе Excel и сортируем по возрастанию. Для выборки без промаха, которую скопировали необходимо снова пересчитать среднее значение и СКО. Результат значений представлен на рисунке 5. Рисунок 5 – Пересчитанные среднее арифметическое и СКО Переходим к проверке о принадлежности к нормальному распределению. Для проверки принадлежности к нормальному распределению нужно построить гистограмму по таблице. Для построения таблицы нужно определить ширину интервала. Количество интервалов выберем 7. Ширина интервалов рассчитывается по формуле: 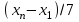 . Левая граница таблицы — это минимальное значение в ряду, правая граница — это минимальное значение и к нему прибавляем значение ширины интервала. Для следующего интервала левая граница будет соответствовать значению правой границы, просто скопировав адрес ячейки. Следует проверить что последнее значение правой границы соответствует максимальному значению в ряду. Далее подсчитываем сколько значений попало в каждый интервал и фиксируем в таблице. По виду гистограммы можно предположить, что она похожа на нормальное распределение, но с уверенностью сказать, нельзя. Таблица и гистограмма приведены на рисунке 6. . Левая граница таблицы — это минимальное значение в ряду, правая граница — это минимальное значение и к нему прибавляем значение ширины интервала. Для следующего интервала левая граница будет соответствовать значению правой границы, просто скопировав адрес ячейки. Следует проверить что последнее значение правой границы соответствует максимальному значению в ряду. Далее подсчитываем сколько значений попало в каждый интервал и фиксируем в таблице. По виду гистограммы можно предположить, что она похожа на нормальное распределение, но с уверенностью сказать, нельзя. Таблица и гистограмма приведены на рисунке 6.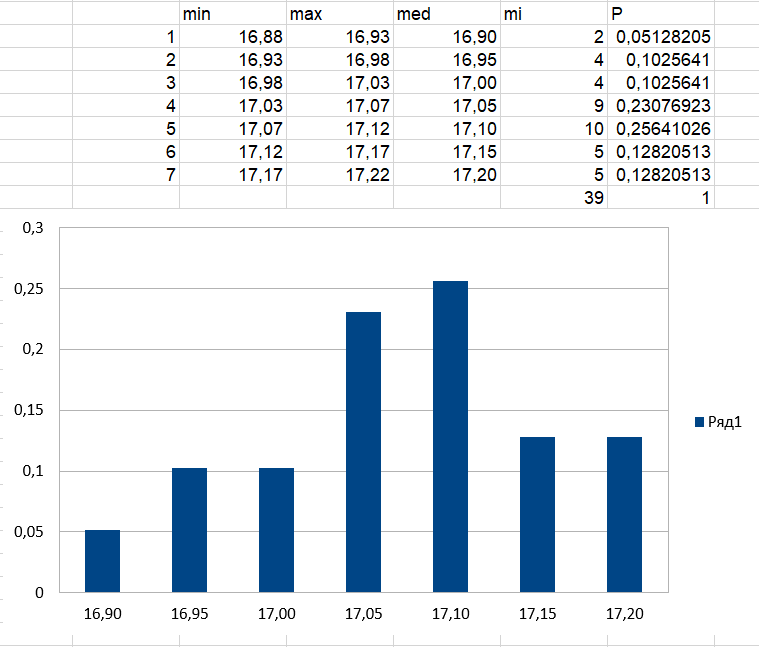 Рисунок 6 – Проверка о принадлежности к нормальному распределению Следующим этапом нужно оценить закон распределения по статистическим критериям. Проводим проверку по первому критерию. Для этого определяется значение d по формуле: 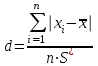 . .Гипотеза о нормальности закона распределения подтверждается, если 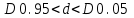 . Проверка гипотезы о принадлежности к нормальному распределению по первому критерию показана на рисунке 7. . Проверка гипотезы о принадлежности к нормальному распределению по первому критерию показана на рисунке 7. Рисунок 7 – Проверка гипотезы о принадлежности к нормальному распределению по первому критерию Выполняем проверку по второму критерию. Гипотеза о нормальности распределения подтверждается, если не более 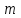 разностей разностей 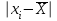 превзошли значения превзошли значения 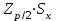 (рисунок 8). (рисунок 8). Рисунок 8 – Проверка гипотезы о принадлежности к нормальному распределению по второму критерию Если гипотеза о принадлежности к нормальному распределению подтвердилась по двум критериям значит результаты принадлежат нормальному распределению. Если они принадлежат нормальному распределению, тогда следующим этапом нужно определить границы доверительного интервала для случайной погрешности. Доверительные границы 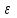 случайной погрешности результата измерения находят по формуле: случайной погрешности результата измерения находят по формуле: 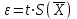 . .Теперь нужно определить границы неисключенной систематической погрешности 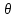 результата измерения, они рассчитывают по формуле: результата измерения, они рассчитывают по формуле: 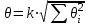 . .Доверительная граница погрешности результата измерения устанавливается в зависимости от соотношения 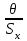 . Если . Если 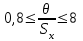 , то доверительные границы погрешности результата измерения вычисляются по формуле: , то доверительные границы погрешности результата измерения вычисляются по формуле: 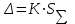 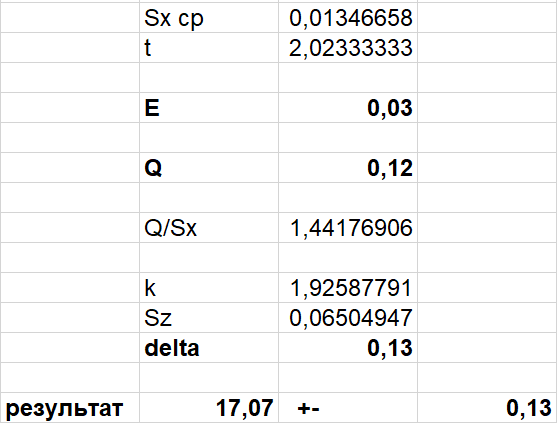 Рисунок 9 – Результаты измерений Выводы: По результатам выполнения лабораторной работы изучены методики выполнения прямых измерений с многократными наблюдениями. Получили навыки стандартной обработки результатов наблюдений, оценивания погрешностей и представления результатов измерений. В ходе выполнения лабораторной работы решены следующие частные задачи: изучен теоретический материал по теме лабораторной работы; Проведена обработка результатов измерений с помощью критериев Романовского, Шарлье и Диксона; проведена оценка полученных результатов измерений; по результатам выполнения лабораторной работы можно сделать выводы о том, что в выборке имеется промах т.к. два критерия из трех, указывают на наличие промаха в выборке. Проверили гипотезу о принадлежности к нормальному распределению по двум критериям, гипотеза о принадлежности к нормальному распределению подтвердилась. СПИСОК ИСПОЛЬЗОВАННЫХ ИСТОЧНИКОВ 1. Пята О.И. Методические указания к лабораторной работе по курсу: “Метрология, стандартизация и сертификация”: СТАНДАРТНАЯ ОБРАБОТКА РЕЗУЛЬТАТОВ ПРЯМЫХ ИЗМЕРЕНИЙ С МНОГОКРАТНЫМИ НАБЛЮДЕНИЯМИ / Бийск: Алт. Гос. техн. ун-т, БТИ, – 8 с. | ||||||||||||||||||||
