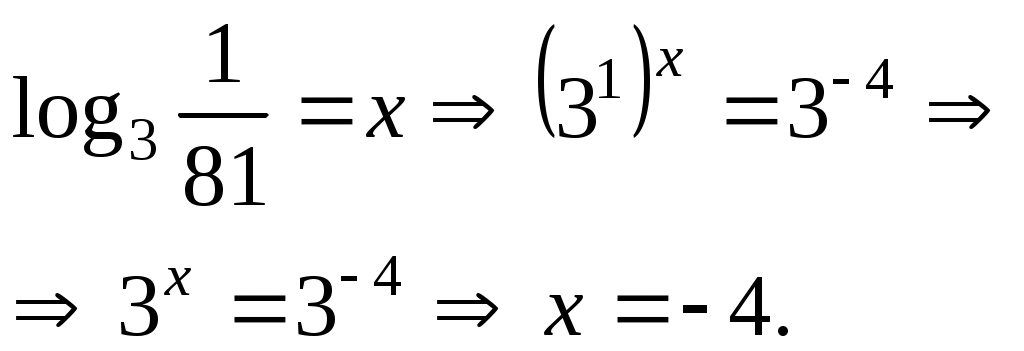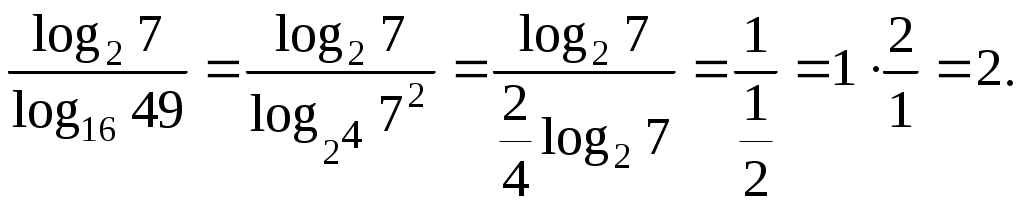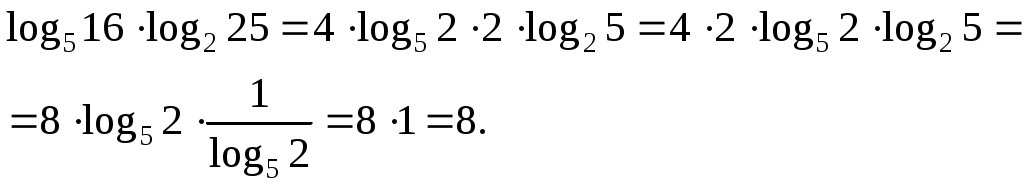|
|
Логарифм. Откуда взялся Log
«Изобретение логарифмов, сократив работу астронома, продлило ему жизнь»
П.С.Лаплас
Откуда взялся Log?
Мы изучили показательные уравнения. Давайте повторим, решив одно из них.
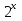 = 32. (1) = 32. (1)
Запишем данное уравнение так: 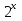 = =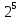 , откуда х = 5. , откуда х = 5.
Напомним, что левую и правую части уравнения удалось представить в виде степени с одним и тем же основанием 2.
А теперь, попробуем решить еще одно показательное уравнение. 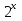 = 30. (2) = 30. (2)
Теперь, тех знаний с точки зрения решения показательных уравнений, недостаточно.
Есть ли корень у этого показательного уравнения? Да, есть.
Как его найти, если уравнение не решается привычным способом?
И теперь, мы введем понятие «логарифм», которое поможет нам решить данное уравнение.
Важно запомнить!
Логарифм (от греч. λόγος – «слово», «отношение», άριθμός - «число») определяется как показатель степени, в которую надо возвести основание, чтобы получить число.
Для начала, представим наши показательные уравнения в виде стандартной формы (т.е. заменим числа с правой и левой стороны на а и b),
напишем: 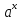 = b. = b.
Важно запомнить!
Корень х уравнения 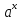 = b будем находить так: = b будем находить так:
х =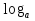 b, где а >0, а b, где а >0, а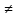 1, b >0. 1, b >0.
Соотнесем теперь определение логарифма с (1) показательным уравнением:
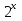 = 32 х = = 32 х =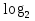 32 32
х = 5, так как 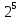 = 32 = 32
Значит, 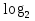 32 = 5, так как 32 = 5, так как 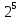 = 32. = 32.
Мы решили показательное уравнение с помощью применение логарифма.
Теперь, представим (2) показательное уравнение в виде логарифма и попробуем решить его: 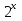 = 30 х = = 30 х =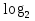 30. 30.
х =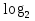 30 – это и есть корень уравнения 30 – это и есть корень уравнения 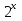 = 30. На инженерном калькуляторе это будет приблизительно. = 30. На инженерном калькуляторе это будет приблизительно.
Так откуда же взялся логарифм? А он взялся из-за потребности решить показательное уравнение, которое не решается привычным способом.
Свойства логарифмов
ТОЖДЕСТВЕННЫЕ ПРЕОБРАЗОВАНИЯ ЛОГАРИФМИЧЕСКИХ И ПОКАЗАТЕЛЬНЫХ ВЫРАЖЕНИЙ
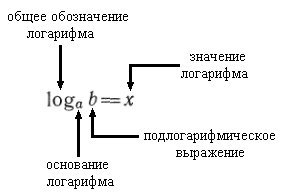
Логарифмом числа bпо основанию а 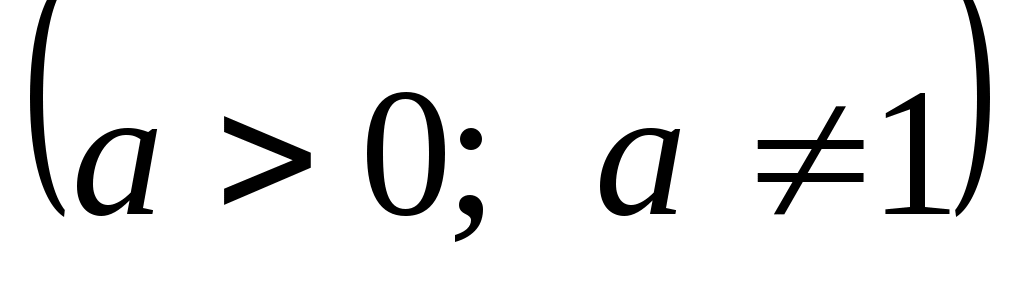 называется показатель степени, в которую надо возвести число а, чтобы получилось b: называется показатель степени, в которую надо возвести число а, чтобы получилось b:
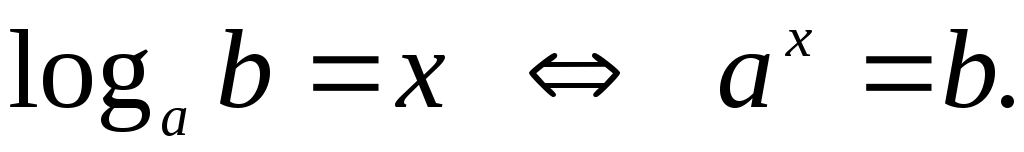
Основное логарифмическое тождество
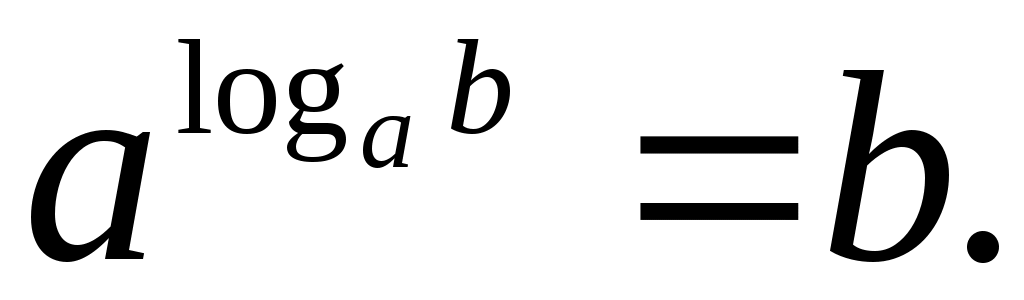
Общая схема вычисления логарифмов.
Она состоит из трех шагов:
Представить основание  и аргумент и аргумент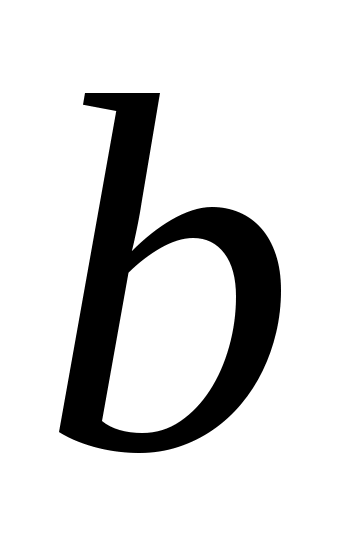 в виде степени с минимально возможным основанием, большим единицы. Попутно лучше избавиться от десятичных дробей; в виде степени с минимально возможным основанием, большим единицы. Попутно лучше избавиться от десятичных дробей;
Решить относительно переменной 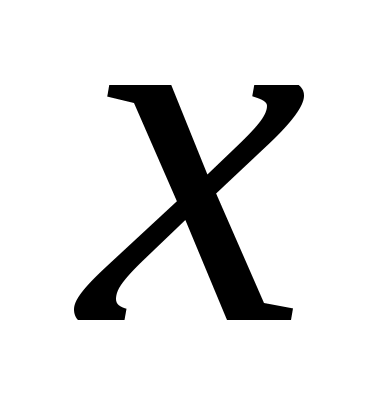 уравнение: уравнение: 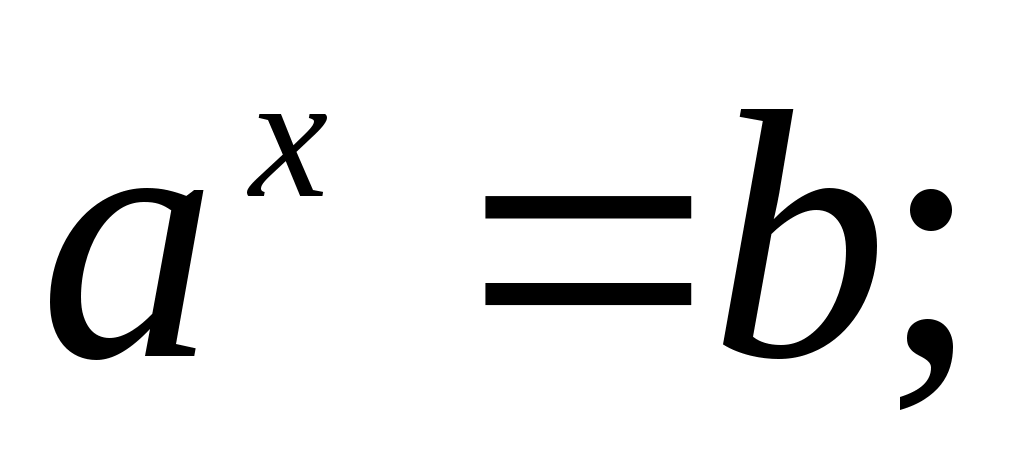
Полученное число 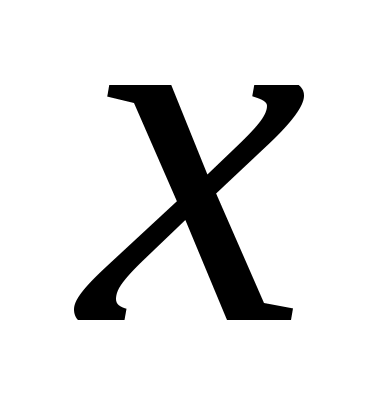 будет ответом. будет ответом.
|
|
Задача
Вычислите логарифм: 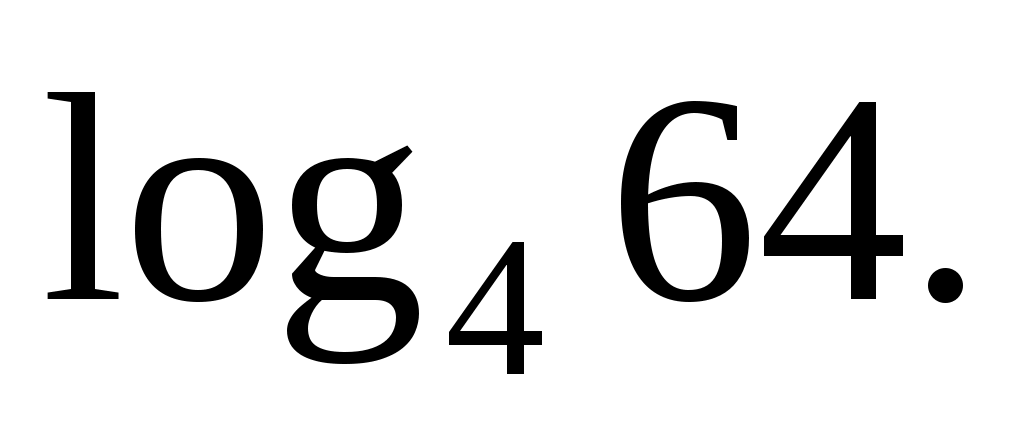
Решение:
Представим основание и аргумент как степень двойки
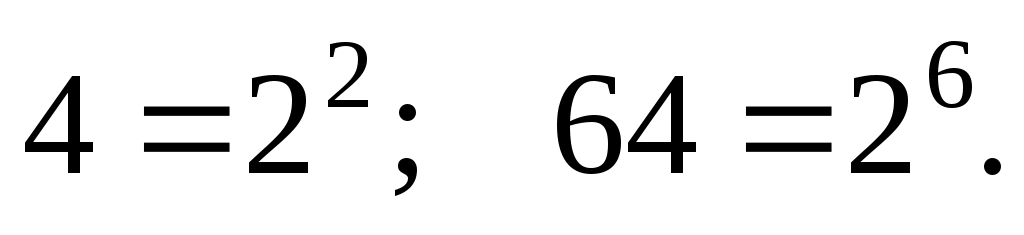
Составим и решим уравнение:
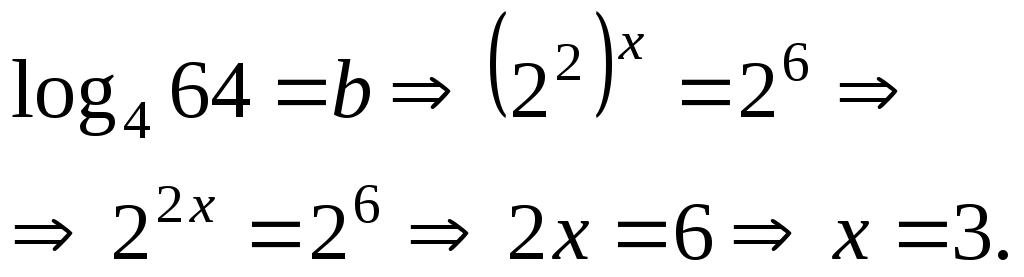
Ответ: 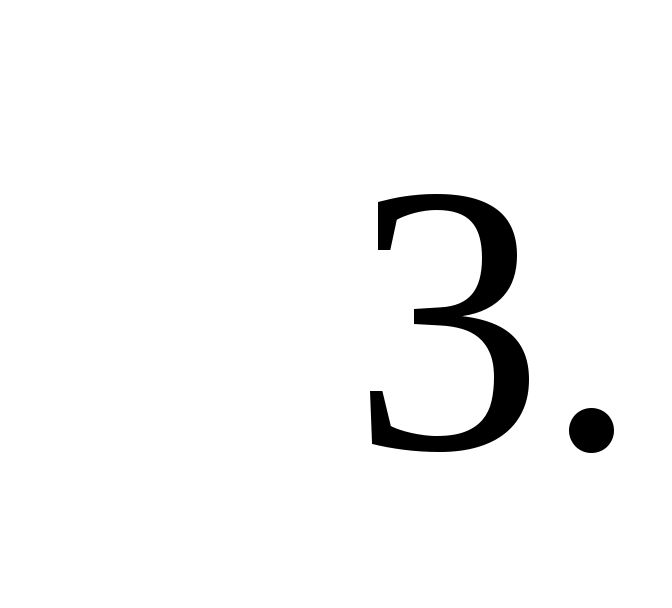
|
Задача
Вычислите логарифм: 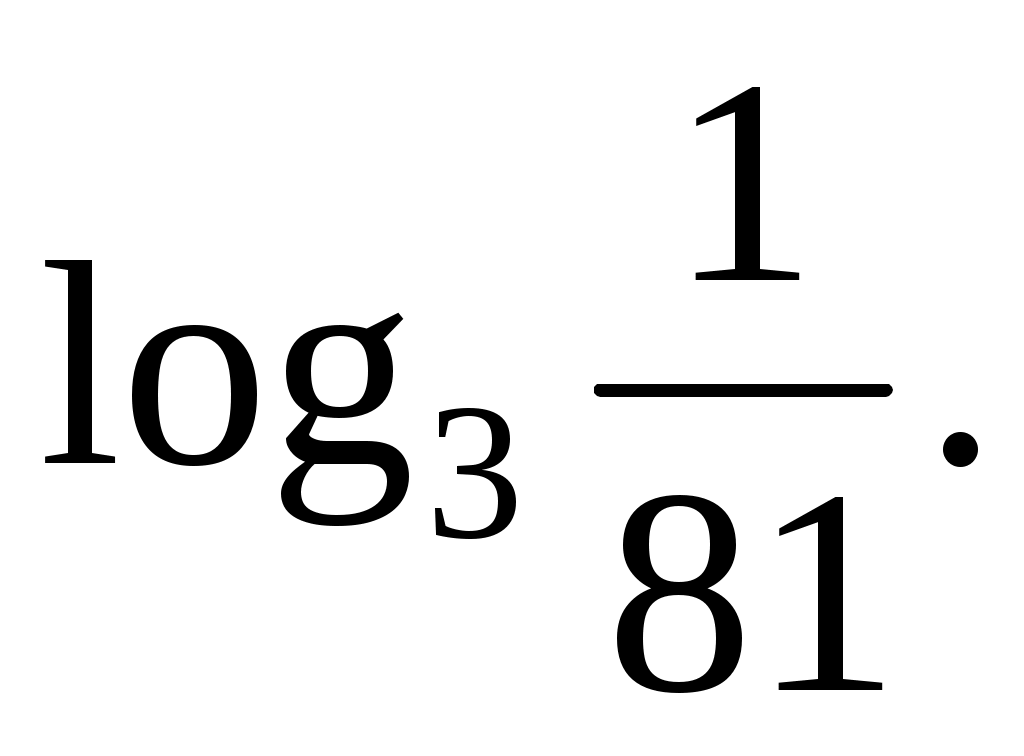
Решение:
Представим основание и аргумент как степень тройки:
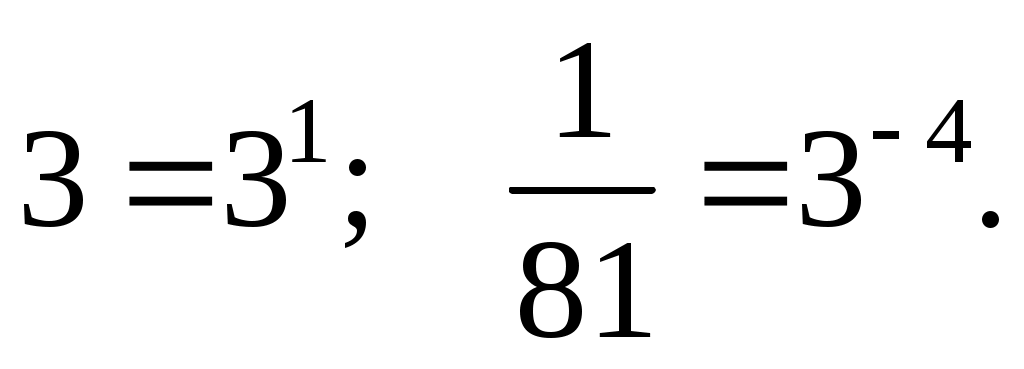
Составим и решим уравнение:
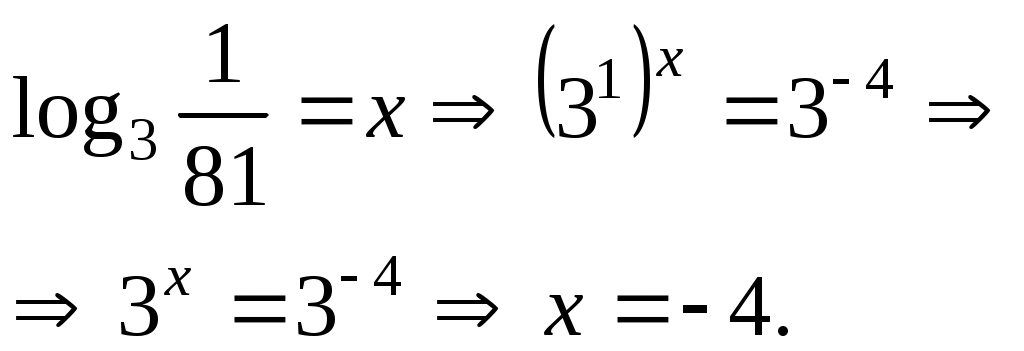
Ответ: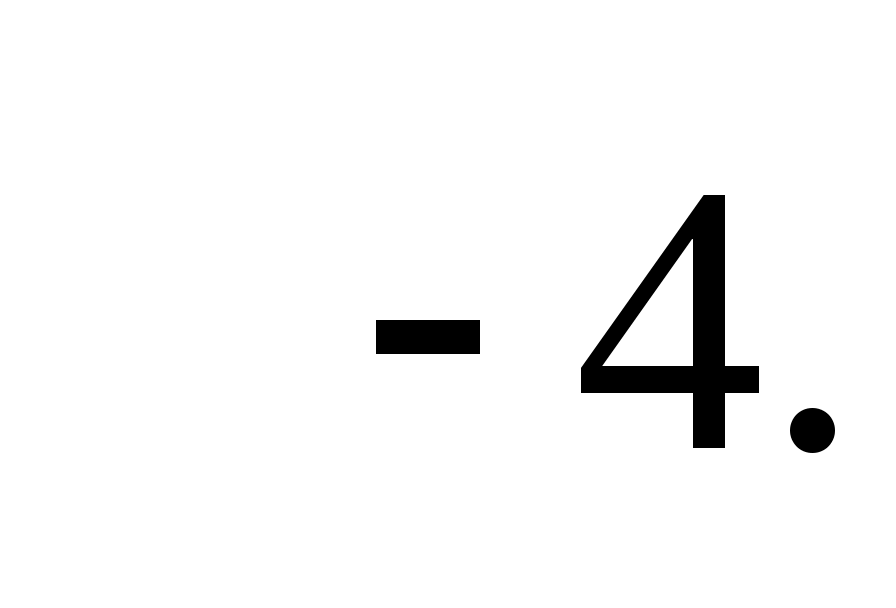
|
Задача
Вычислите логарифм: 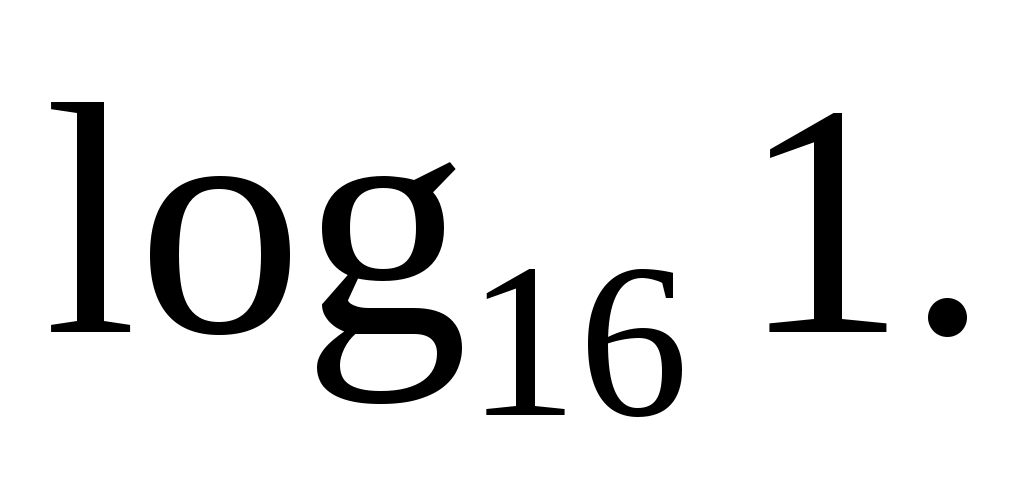
Решение:
Представим основание и аргумент как степень двойки
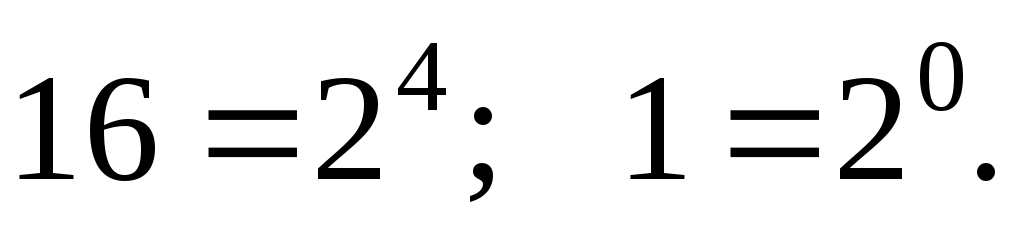
Составим и решим уравнение:
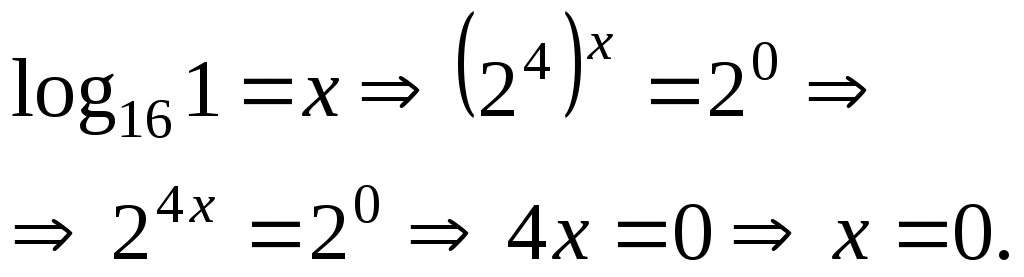
Ответ: 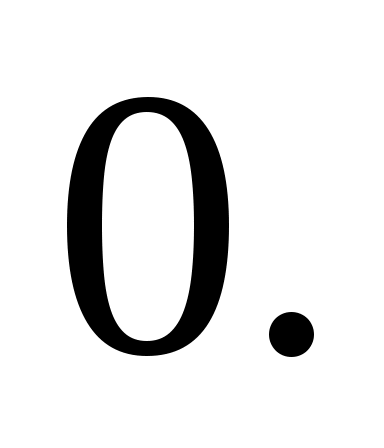
|
Задача
Вычислите логарифм: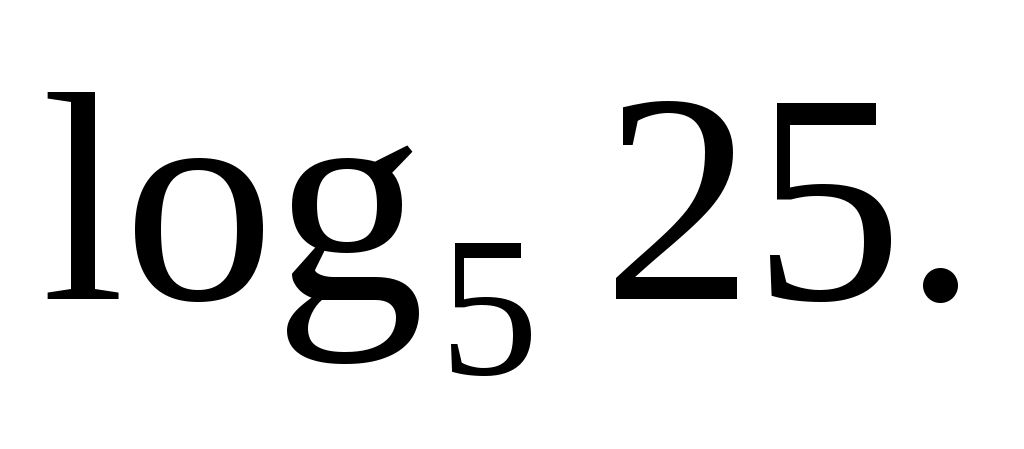
Решение:
Представим основание и аргумент как степень пятерки:
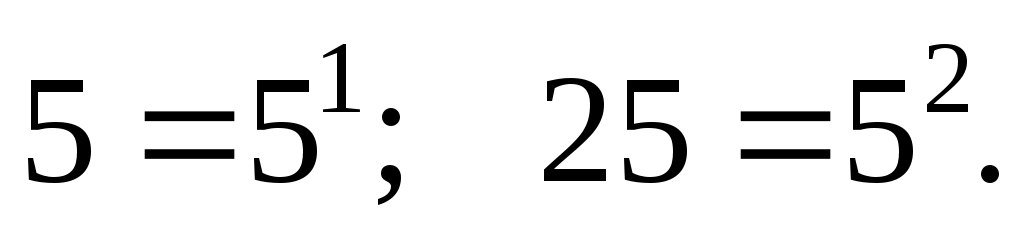
Составим и решим уравнение:
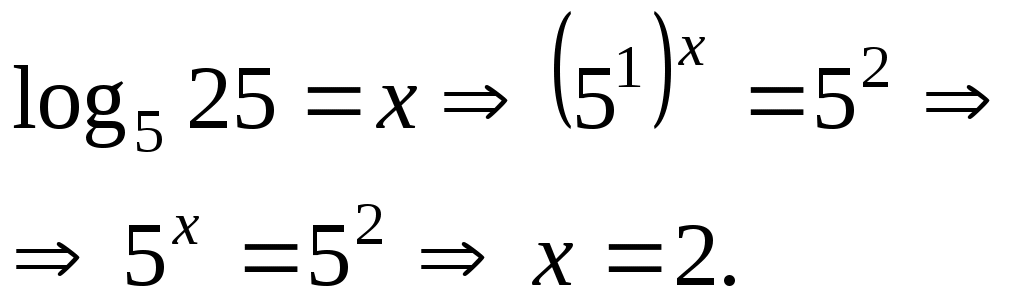
Ответ: 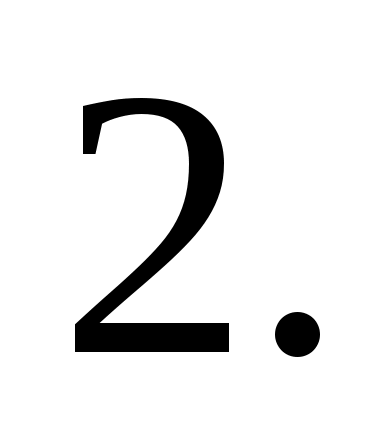
|
Задача
Вычислите логарифм: 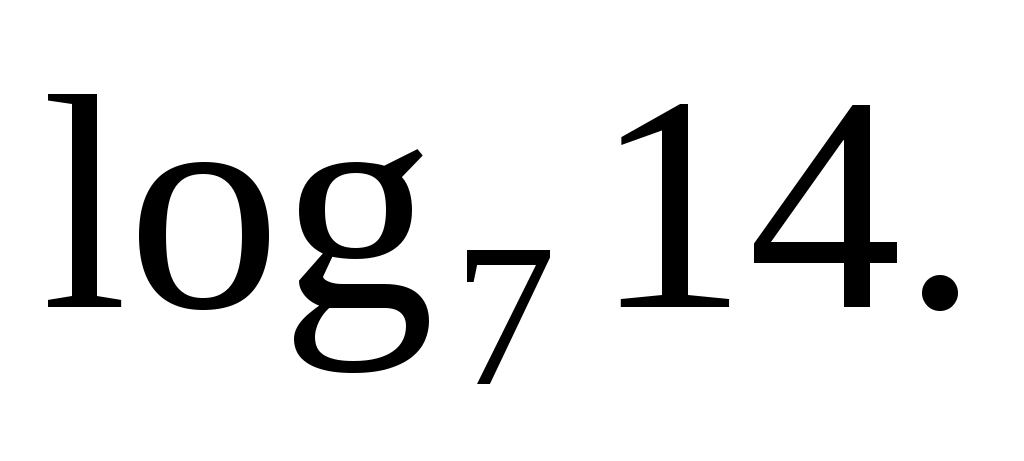
Решение:
Представим основание и аргумент как степень семерки:
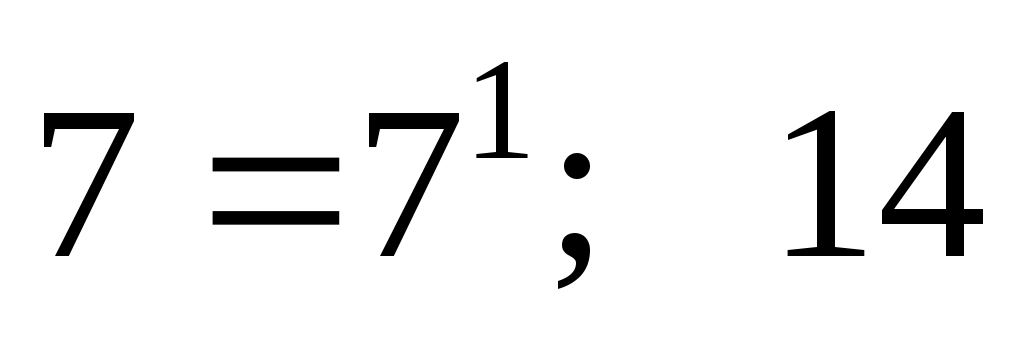 в виде степени семерки не представляется, поскольку в виде степени семерки не представляется, поскольку 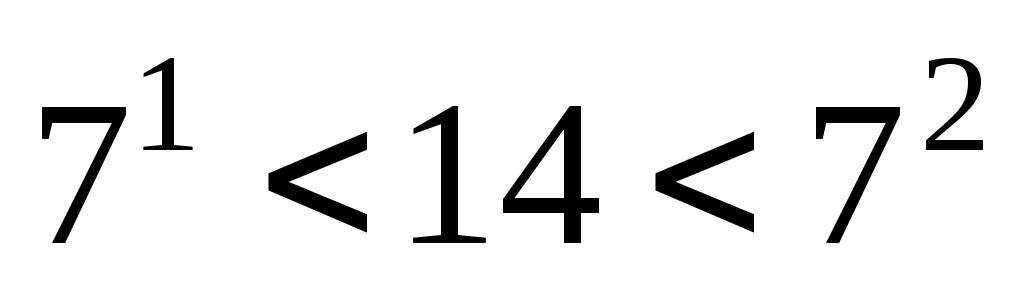 следует, что логарифм не считается. следует, что логарифм не считается.
Ответ: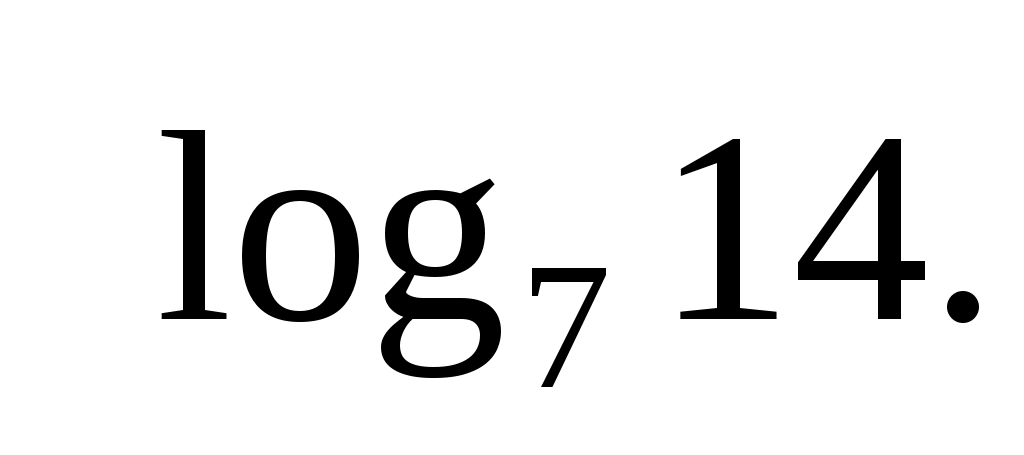
| Свойства логарифмов (образцы решения)
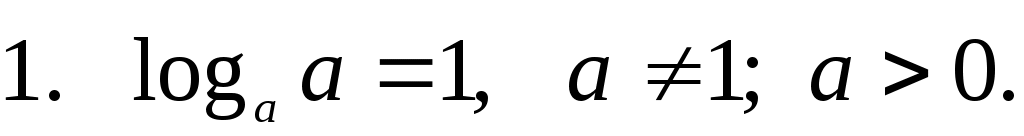
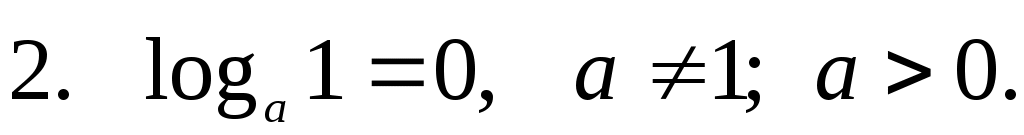
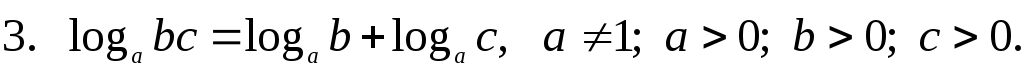
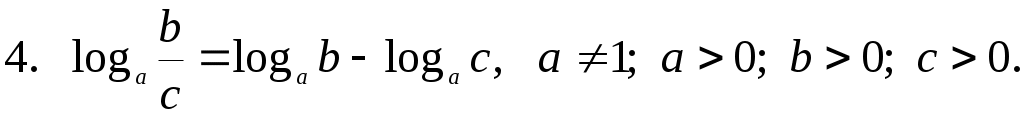
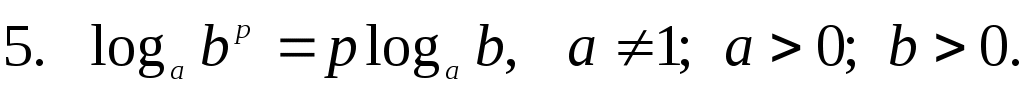
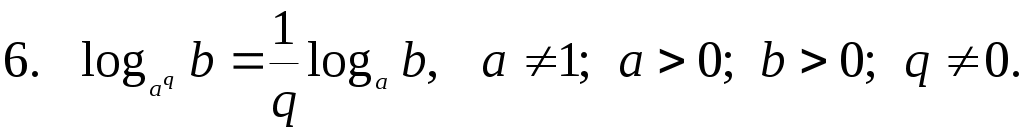
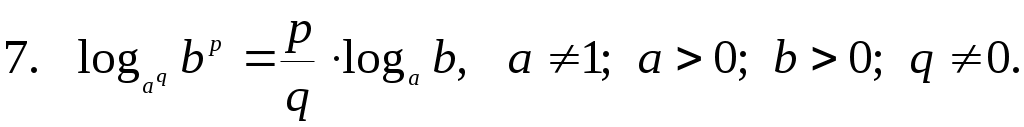
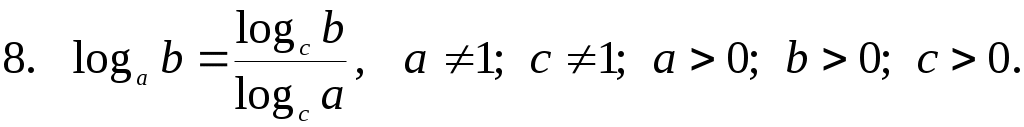
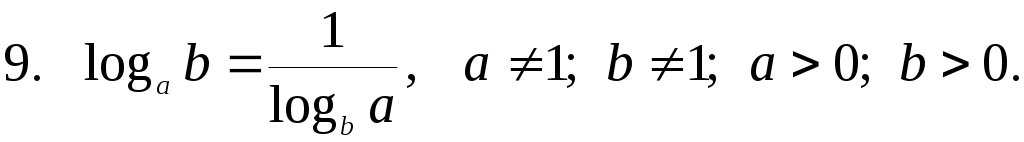
Другие виды обозначения логарифмов:
логарифм числа b по основанию e
(натуральный логарифм)
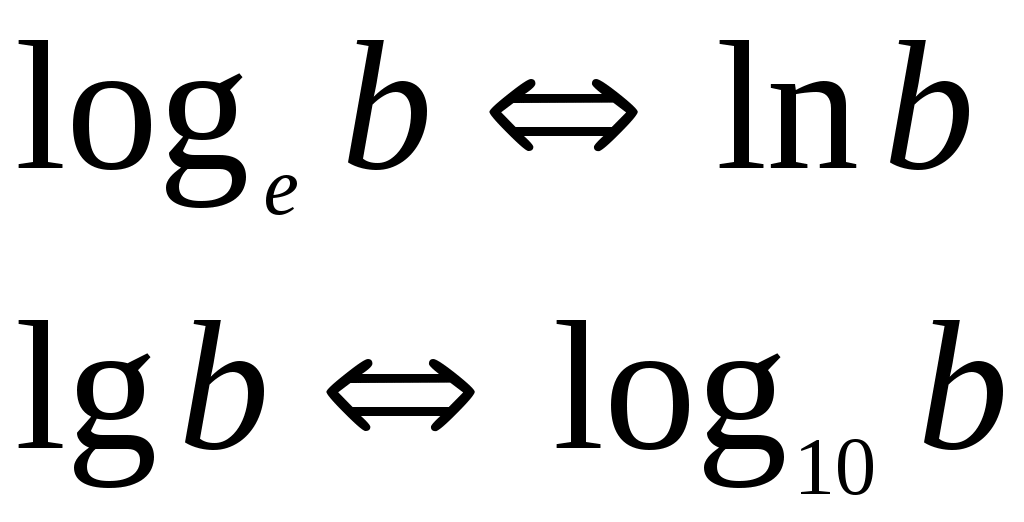
e = 2,718281828459045… – основание натурального логарифма;
логарифм числа b по основанию 10
(десятичный логарифм)
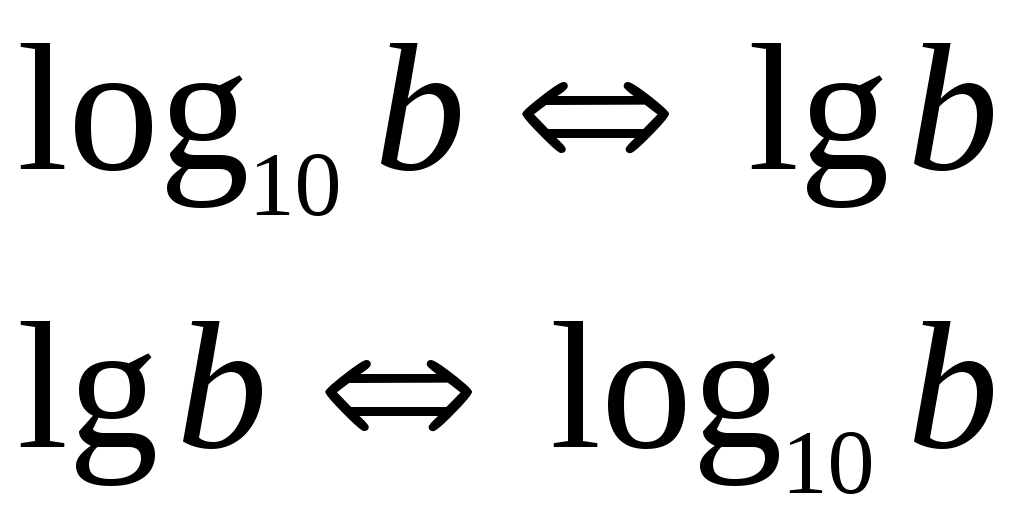
10 – основание десятичного логарифма.
Логарифмическая единица
и логарифмический ноль
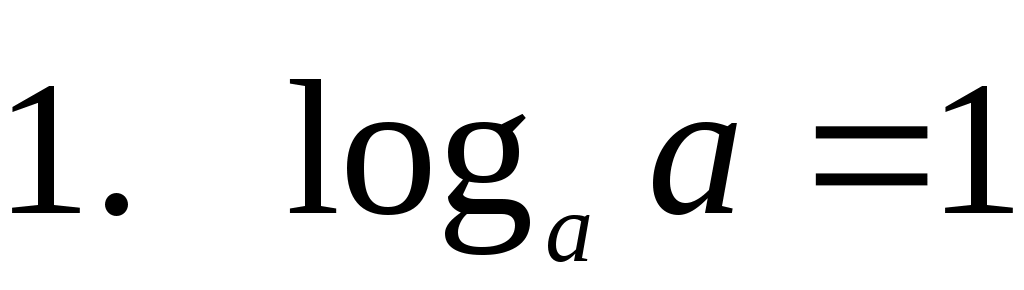 — это логарифмическая единица. — это логарифмическая единица.
Запомните раз и навсегда:
логарифм по любому основанию  от самого этого основания равен единице. от самого этого основания равен единице.
Например: 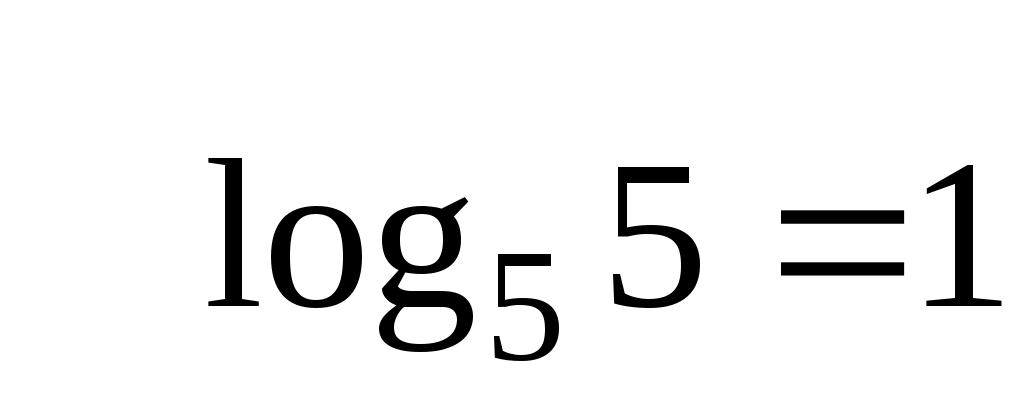 . .
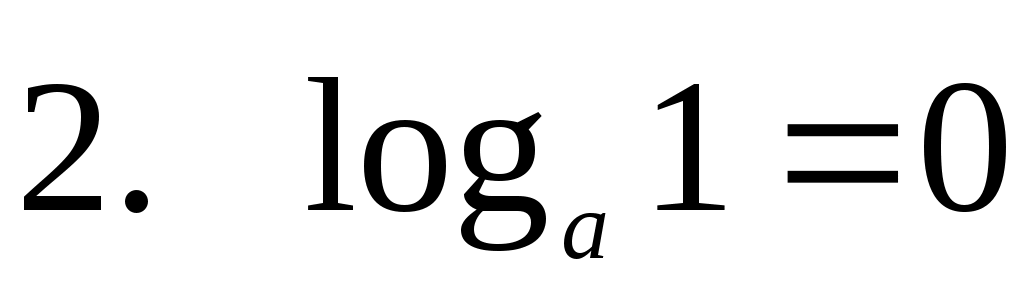 — это логарифмический ноль. — это логарифмический ноль.
Основание  может быть каким угодно, но если в аргументе стоит единица — логарифм равен нулю! Потому, что может быть каким угодно, но если в аргументе стоит единица — логарифм равен нулю! Потому, что 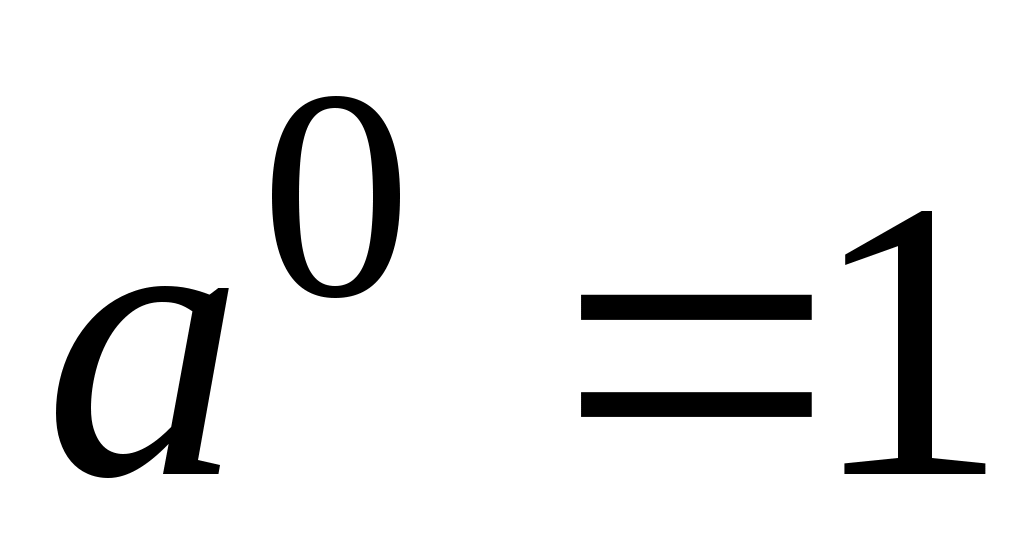 — это прямое следствие из определения. — это прямое следствие из определения.
Например: 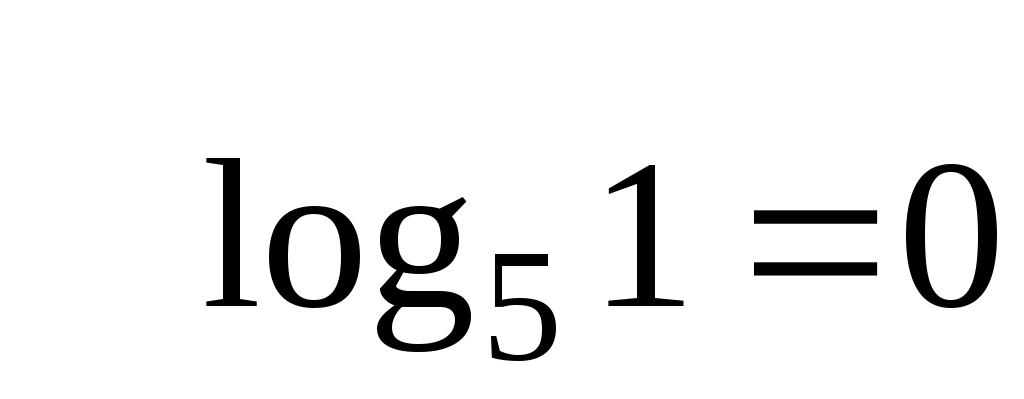 . .
Сложение и вычитание логарифмов
|
Итак, сумма логарифмов равна логарифму произведения,
а разность — логарифму частного.
Обратите внимание:
ключевой момент здесь — одинаковые основания.
Если основания разные, эти правила не работают.
|
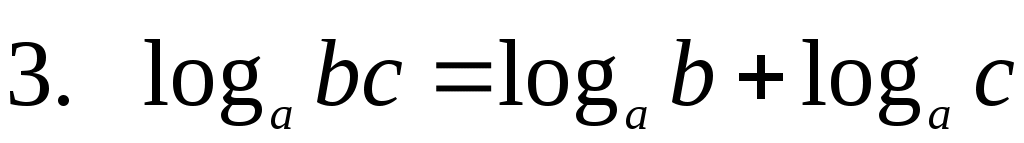
|
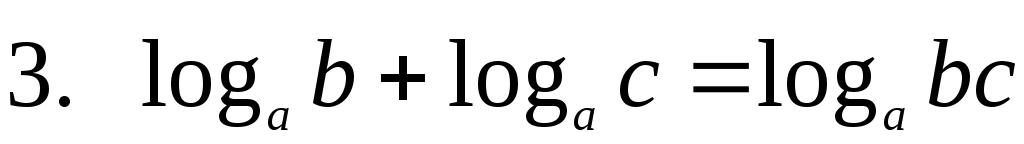
|
Задача
Представьте логарифм в виде суммы: 
Решение:
Представим число 14 в виде произведения  и применим формулу суммы: и применим формулу суммы:

Ответ: 
|
Задача
Найдите значение выражения: 
Решение:
Поскольку основания у логарифмов одинаковые, используем формулу суммы:

Ответ: 
|
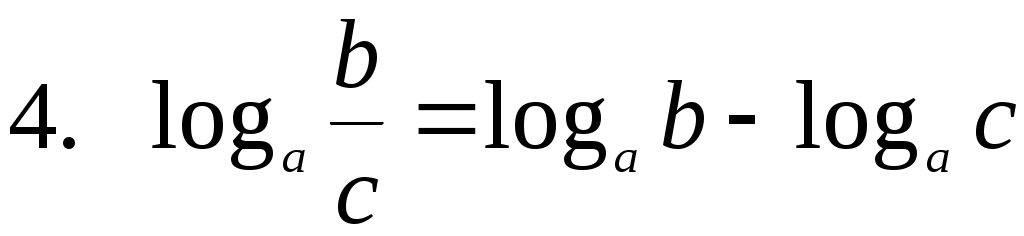
|
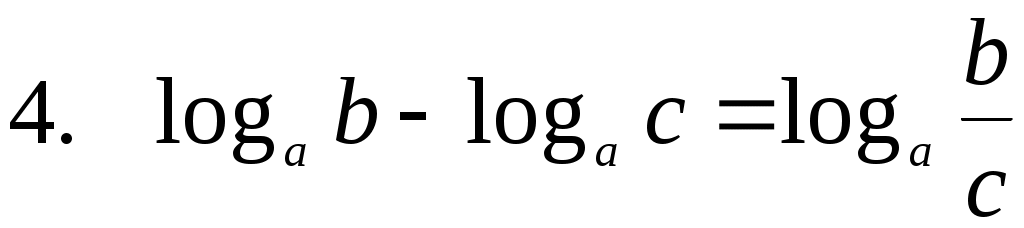
|
Задача
Представьте логарифм в виде разности: 
Решение:
Представим число 0,4 в виде обыкновенной дроби и применим формулу разности:

Ответ: 
|
Задача
Найдите значение выражения: 
Решение:
Поскольку основания у логарифмов одинаковые, используем формулу разности:

Ответ: 
|
Вынесение показателя степени из логарифма
|
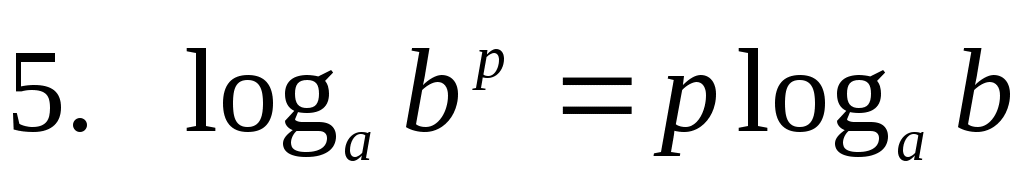
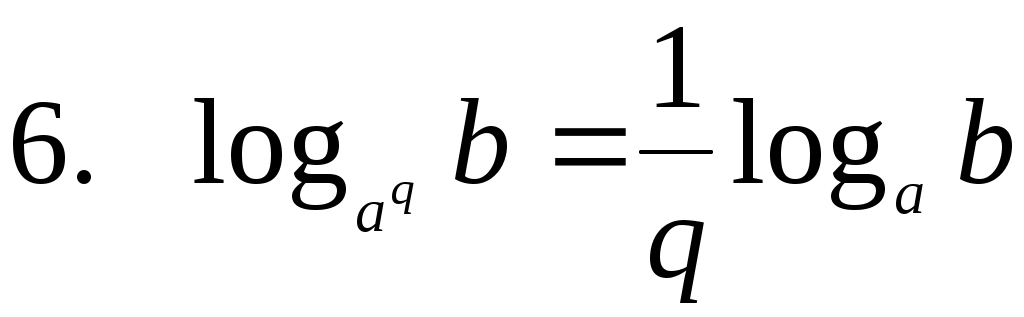
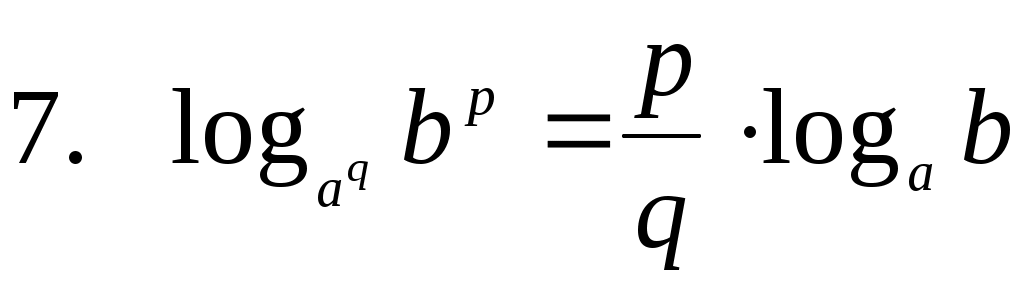
|
Задача
Найдите значение выражения: 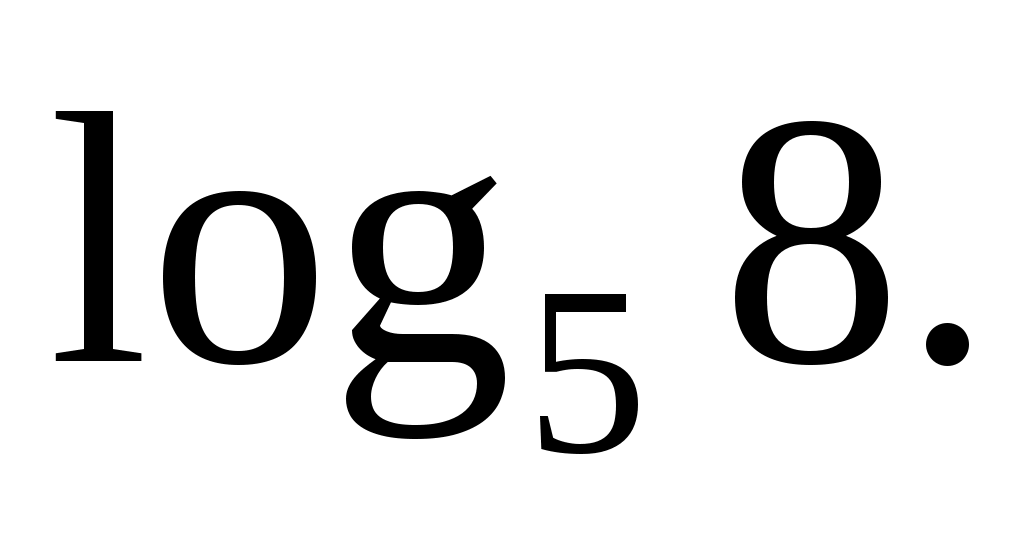
Решение:
Избавимся от степени в аргументе по пятой формуле:
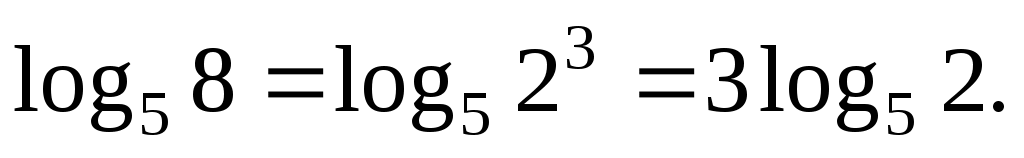
Ответ: 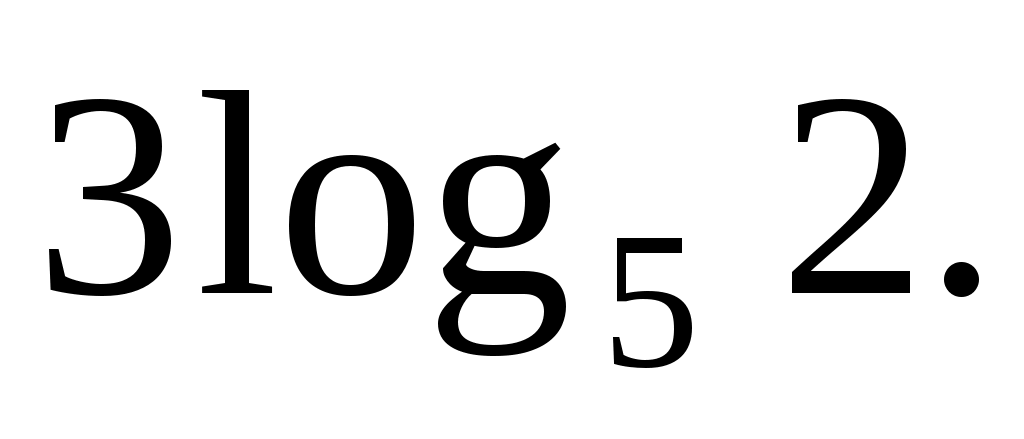
|
Задача
Найдите значение выражения: 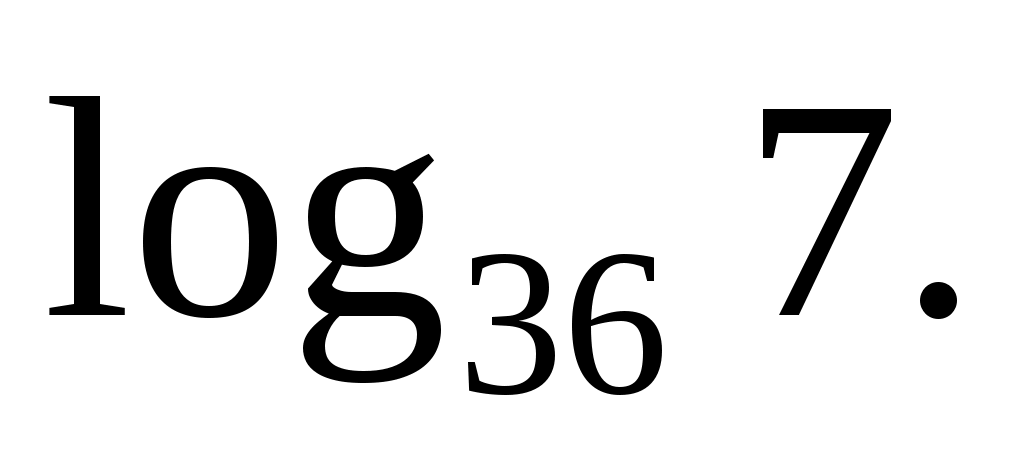
Решение:
Избавимся от степени в основании по шестой формуле:
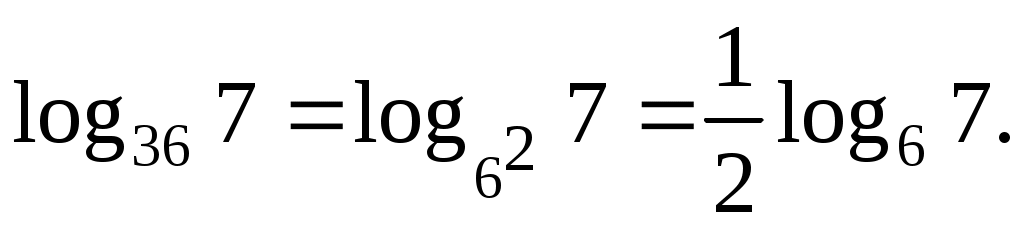
Ответ: 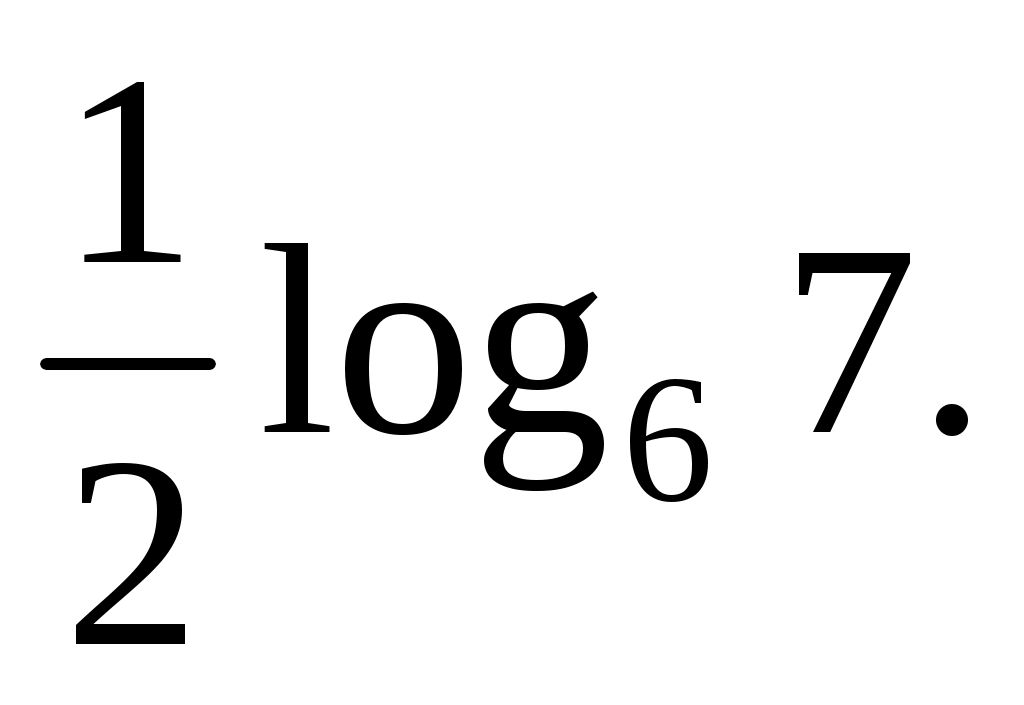
|
Задача
Найдите значение выражения: 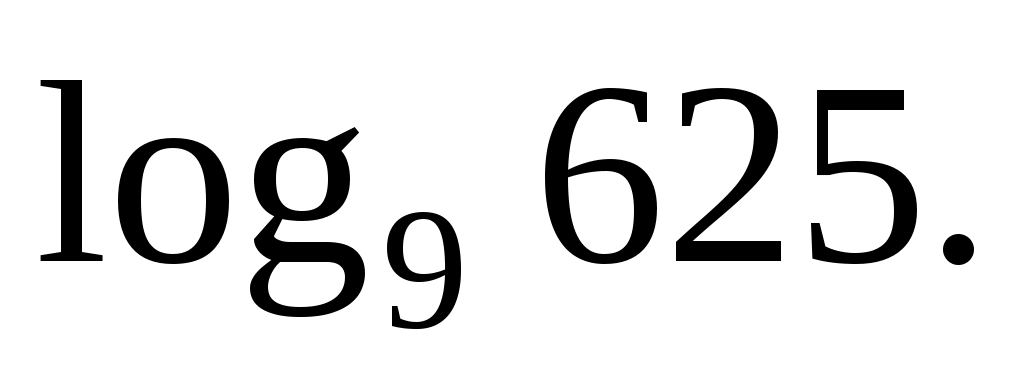
Решение:
Избавимся от степени в аргументе и основании по седьмой формуле:
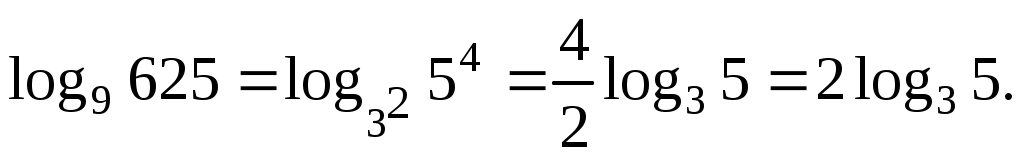 Ответ: Ответ: 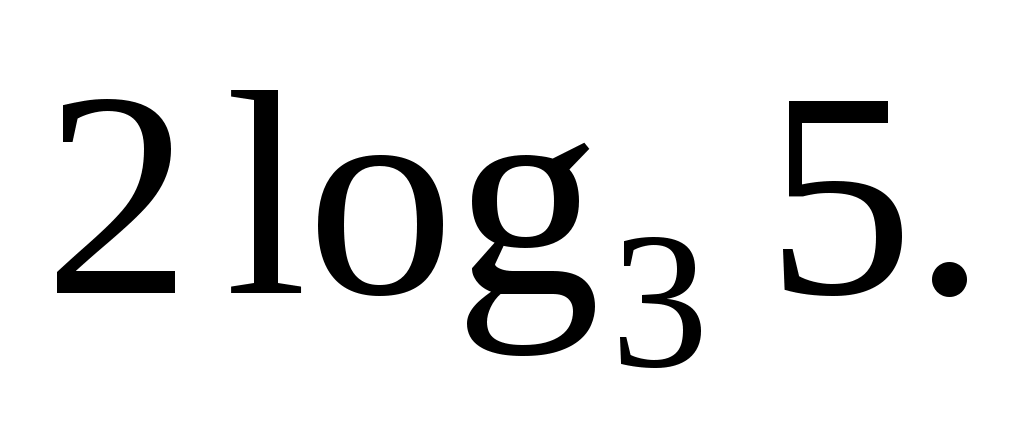
|
Задача
Найдите значение выражения: 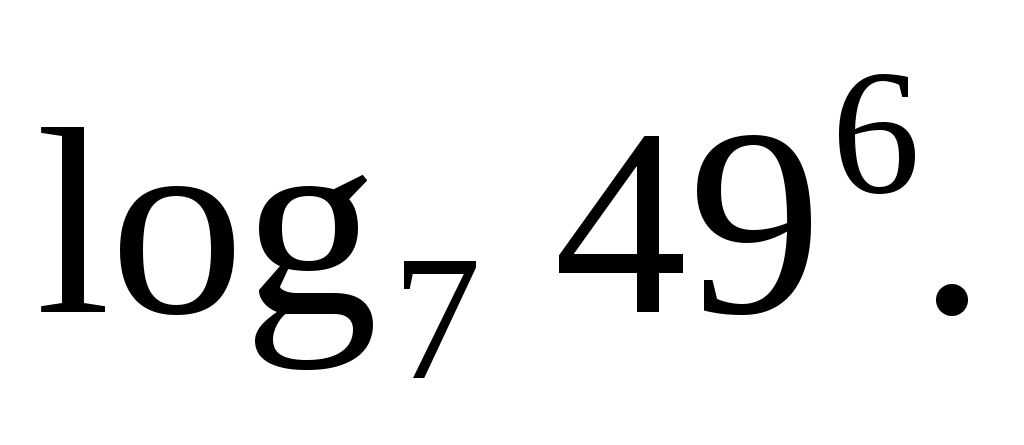
Решение:
Избавимся от степени в аргументе по пятой формуле:
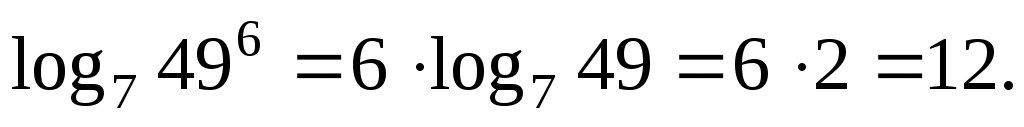
Ответ: 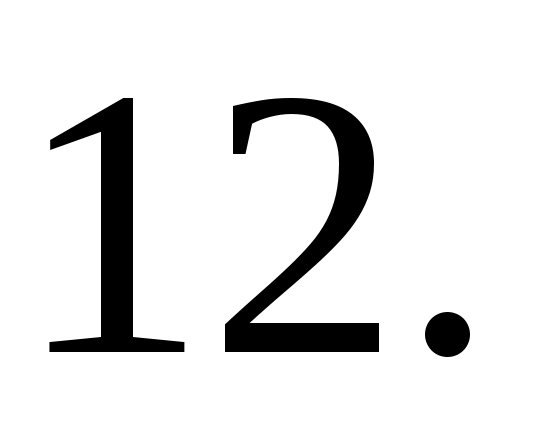
|
Задача
Найдите значение выражения: 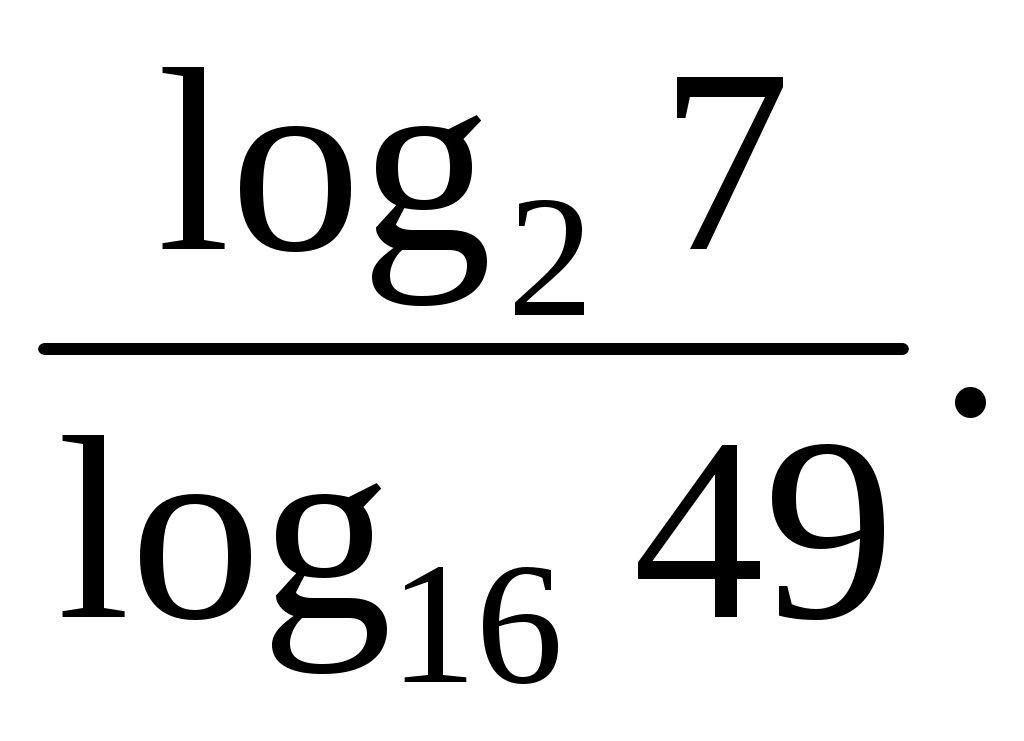
Решение:
Заметим, что в знаменателе стоит логарифм, основание и аргумент которого являются точными степенями: 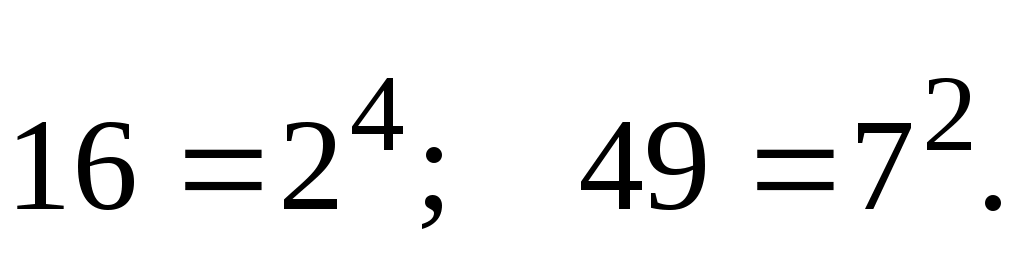 Имеем: Имеем:
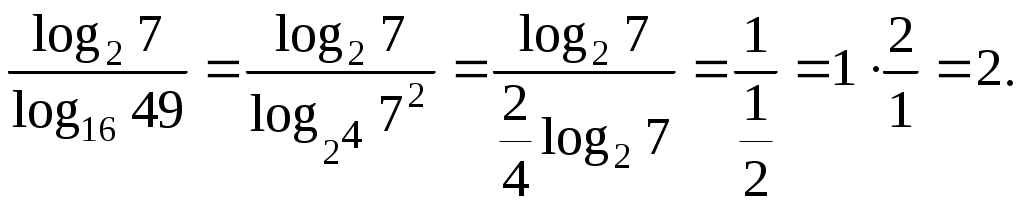
Ответ: 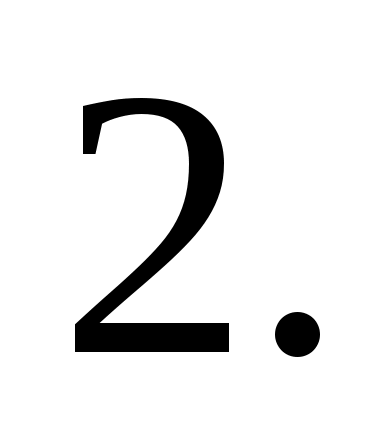
|
Задача
Найдите значение выражения: 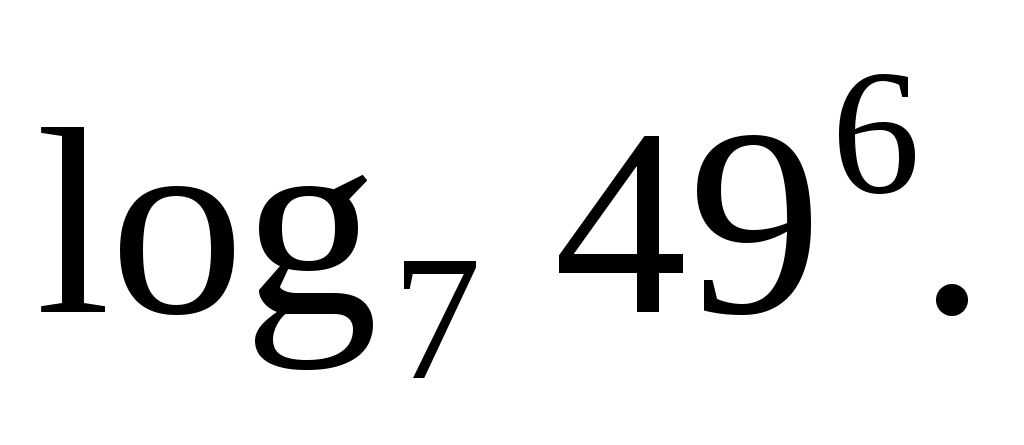
Решение:
Избавимся от степени в аргументе по пятой формуле:
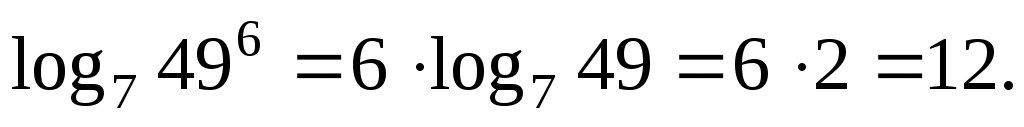
Ответ: 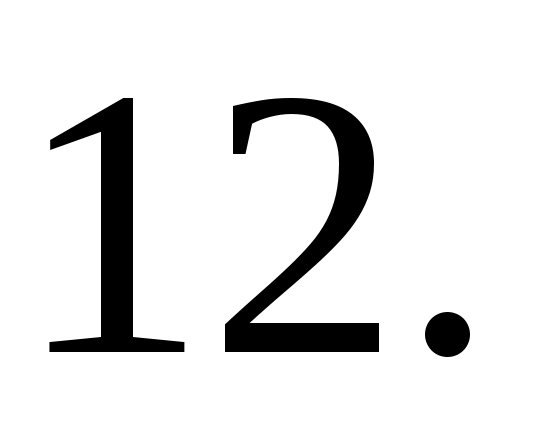
|
Задача
Найдите значение выражения: 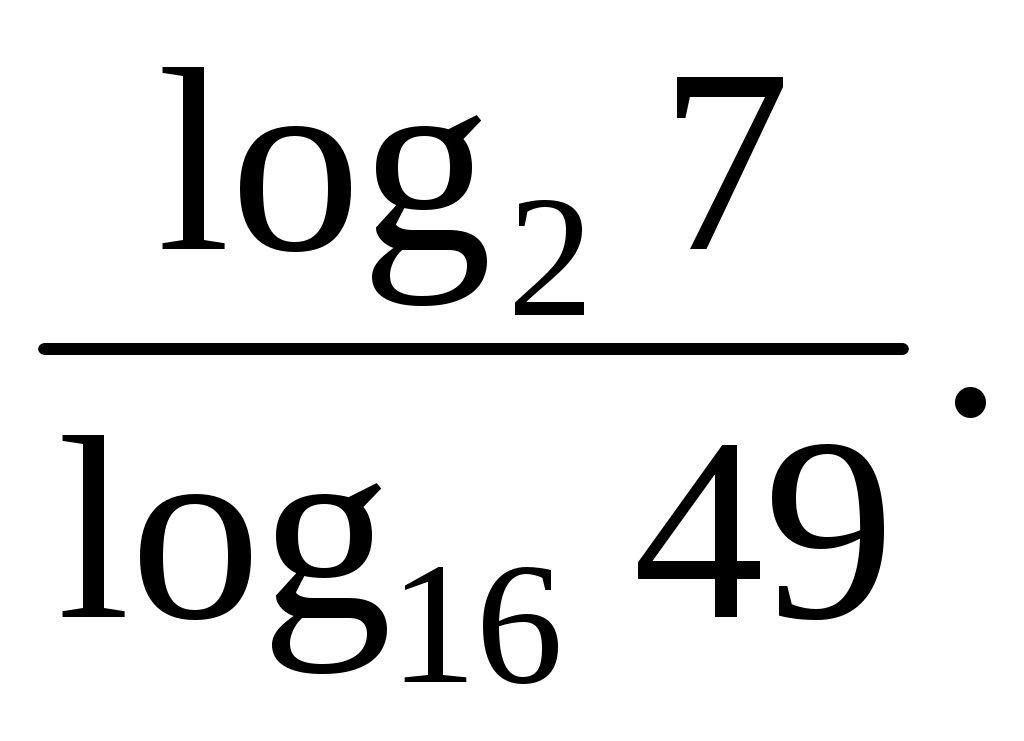
Решение:
Заметим, что в знаменателе стоит логарифм, основание и аргумент которого являются точными степенями: 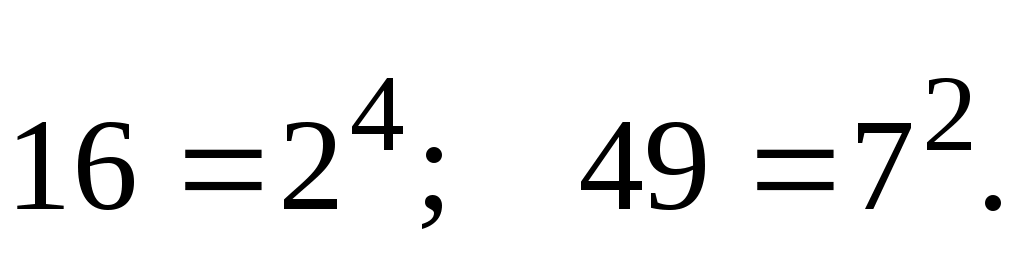 Имеем: Имеем:
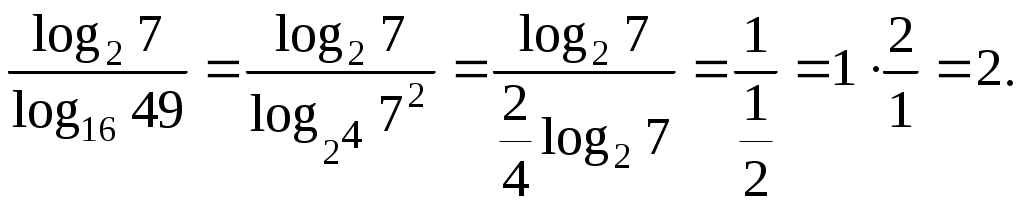
Ответ: 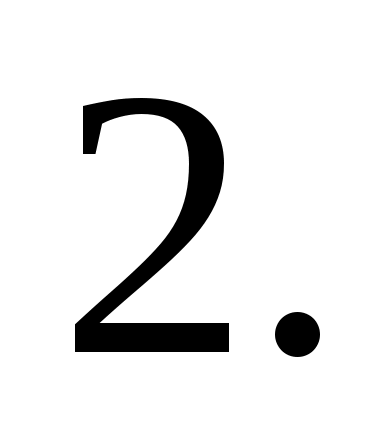
|
Переход к новому основанию
|
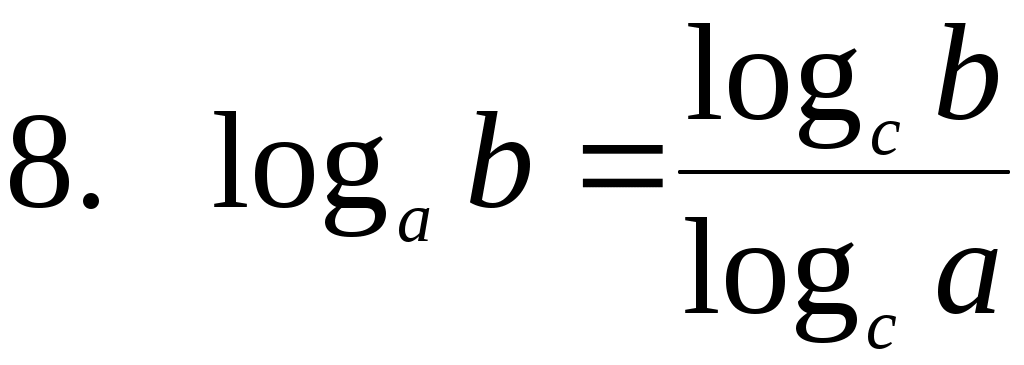
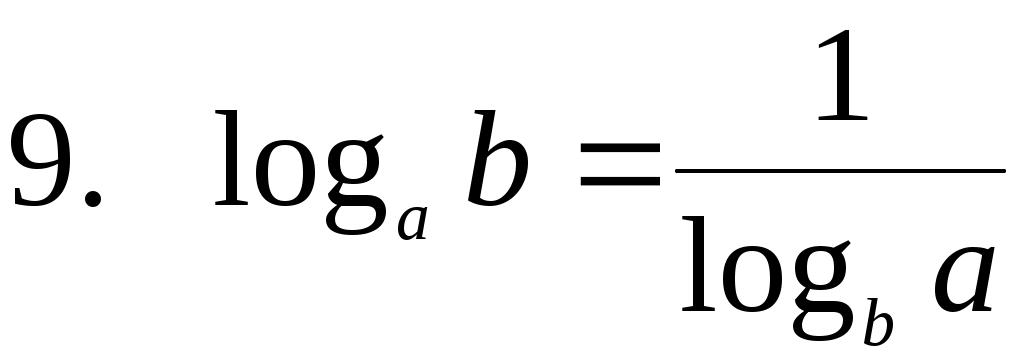
|
Из девятой формулы следует, что можно менять местами основание и аргумент логарифма, но при этом все выражение «переворачивается», т.е. логарифм оказывается в знаменателе.
|
Задача
Представьте 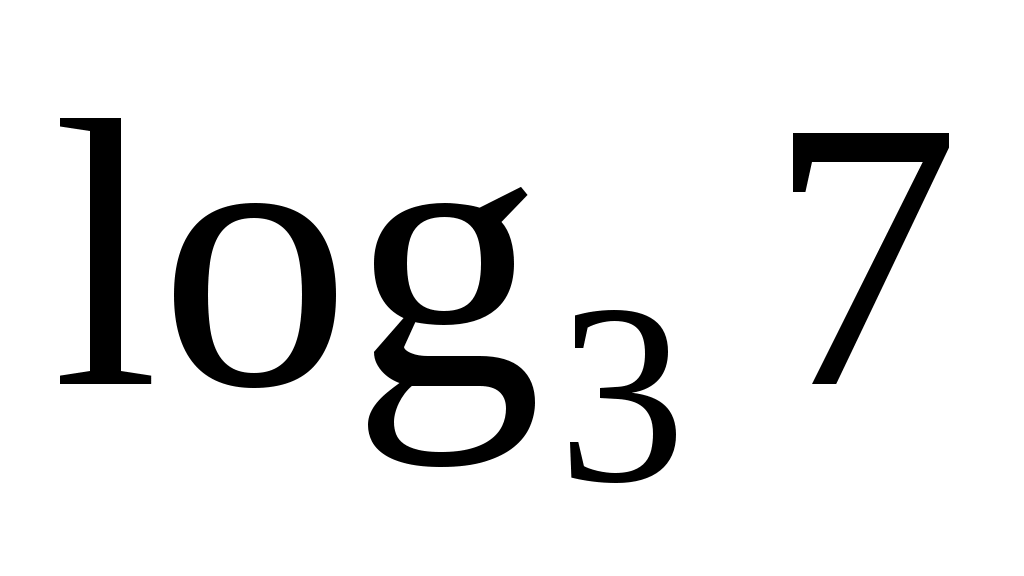 в виде логарифма с основанием 2. в виде логарифма с основанием 2.
Решение:
Воспользуемся восьмой формулой:
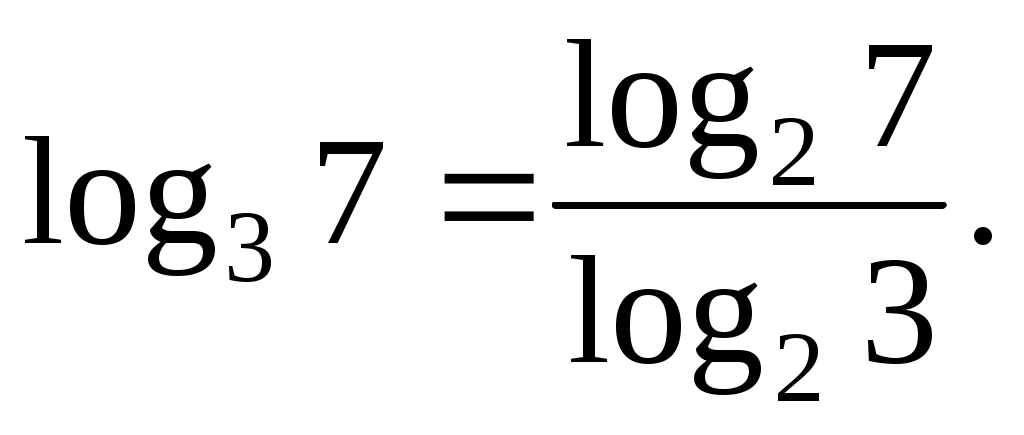
Ответ: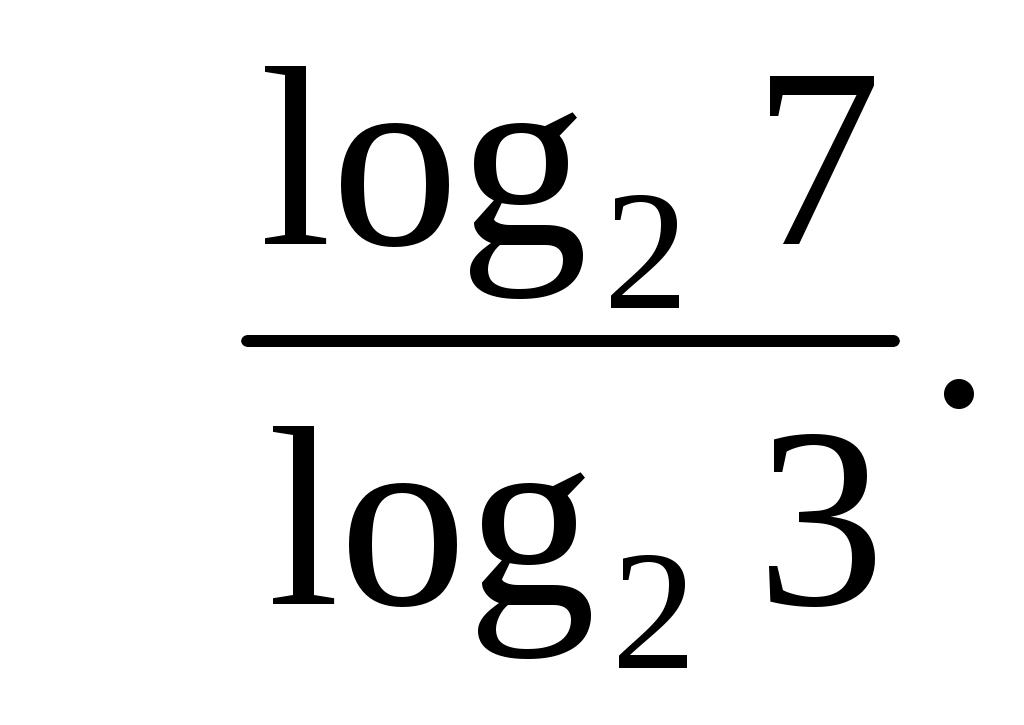
|
Задача
Представьте 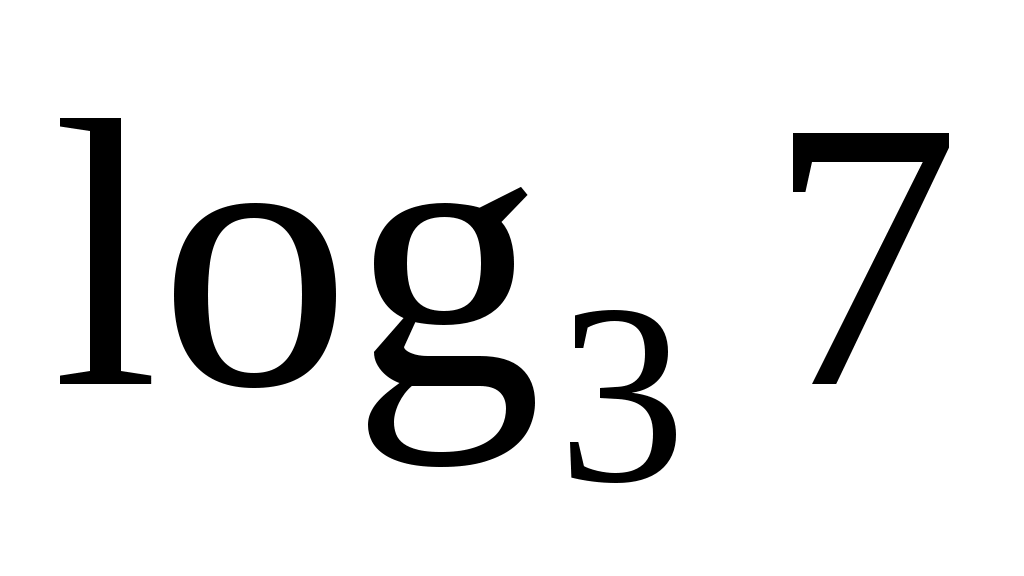 в виде логарифма с основанием 7. в виде логарифма с основанием 7.
Решение:
Воспользуемся девятой формулой:
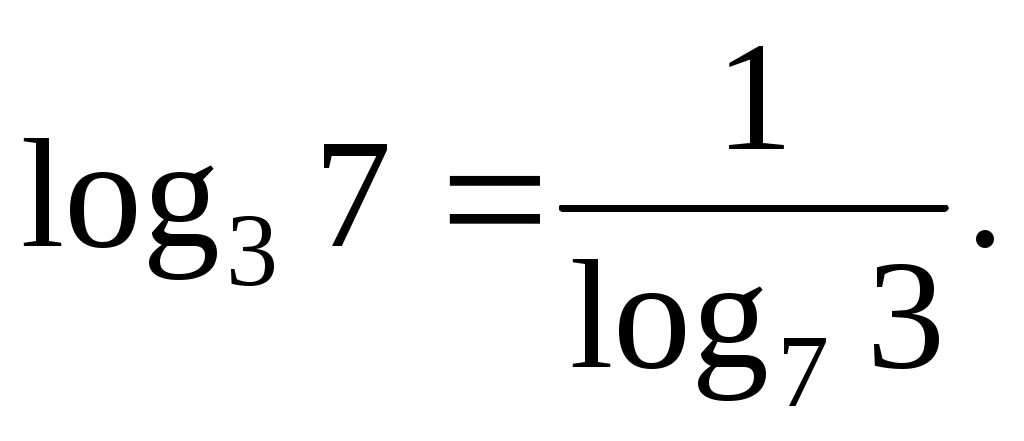
Ответ: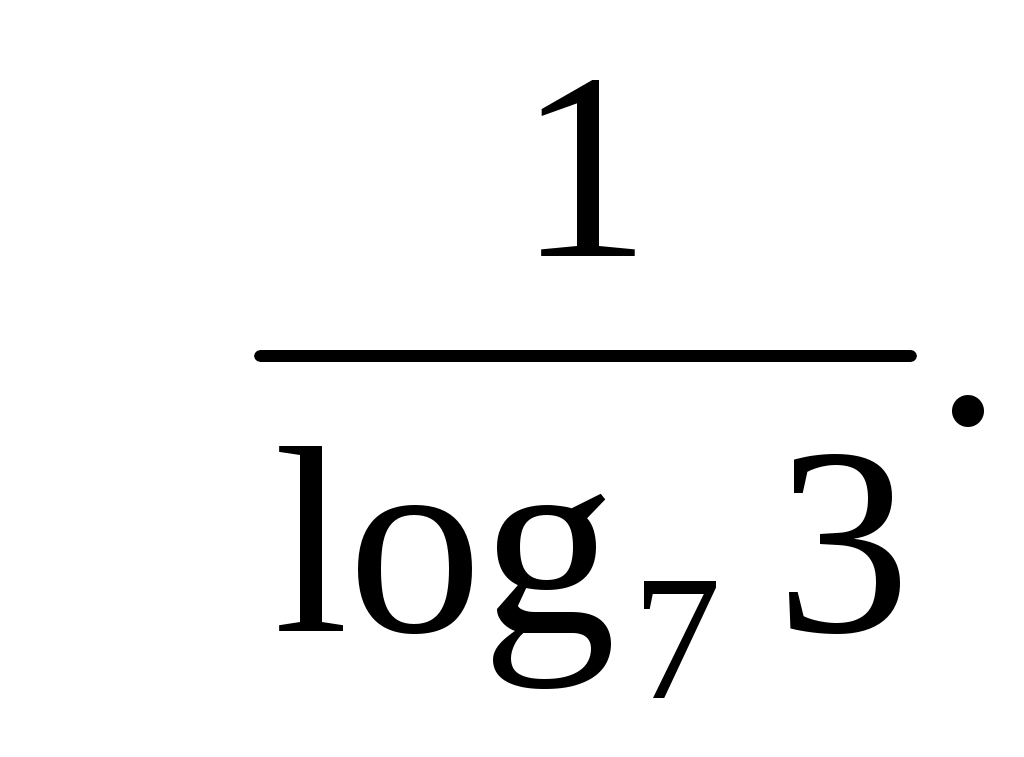
|
Задача
Найдите значение выражения: 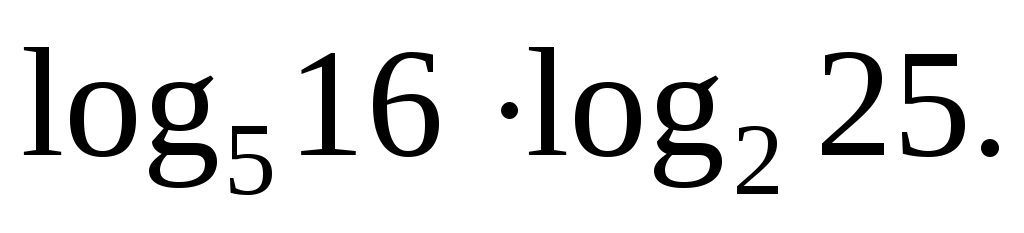
Решение:
Заметим, что в аргументах обоих логарифмов стоят точные степени. Вынесем показатели:
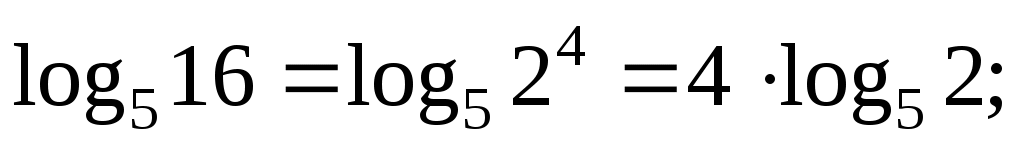
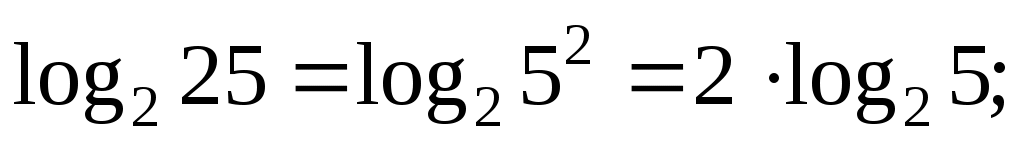
А теперь «перевернем» второй логарифм:
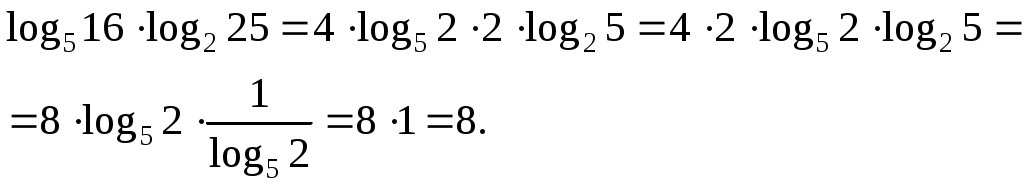
Поскольку от перестановки множителей произведение не меняется, мы спокойно перемножили четверку и двойку, а затем разобрались с логарифмами.
Ответ: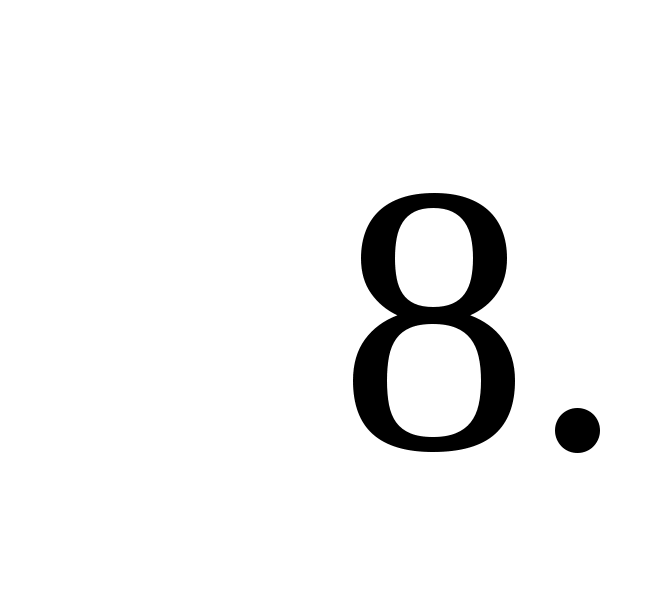
|
Задача
Найдите значение выражения: 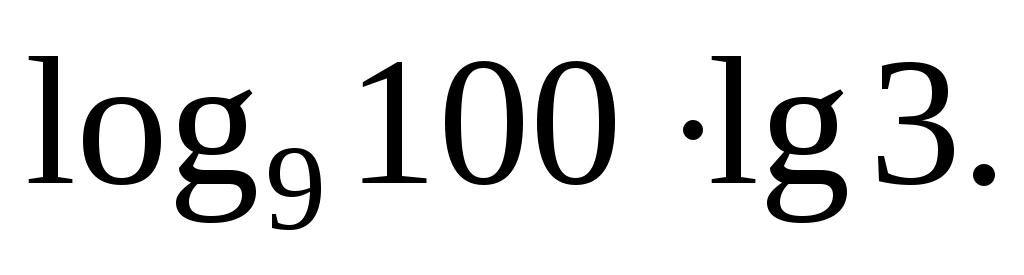
Решение:
Основание и аргумент первого логарифма — точные степени. Запишем это и избавимся от показателей:
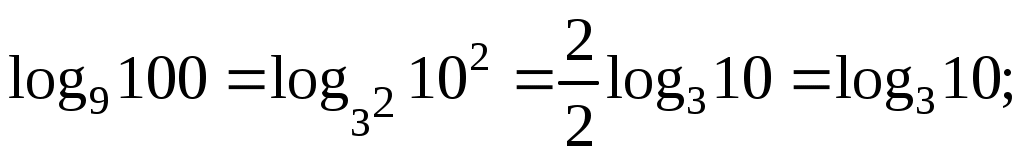
Теперь избавимся от десятичного логарифма, перейдя к новому основанию:
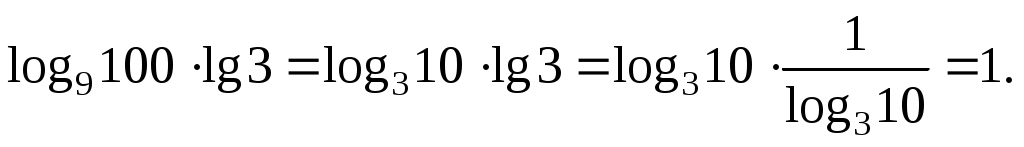
Ответ: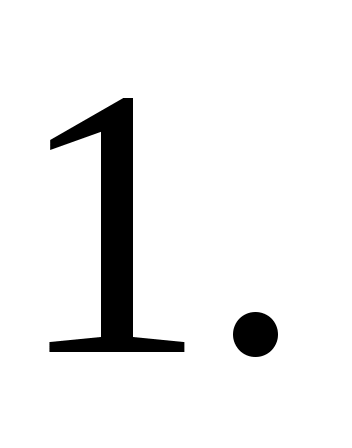
|
Основное логарифмическое тождество
|
Часто в процессе решения требуется представить число как логарифм по заданному основанию. В этом случае нам помогут формулы:
|
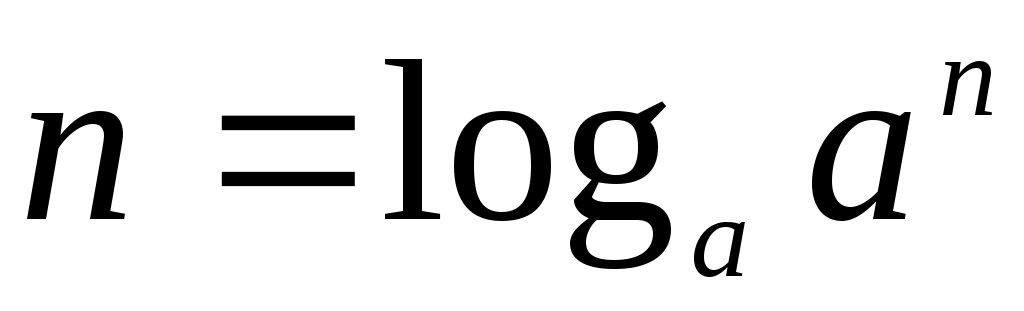
|
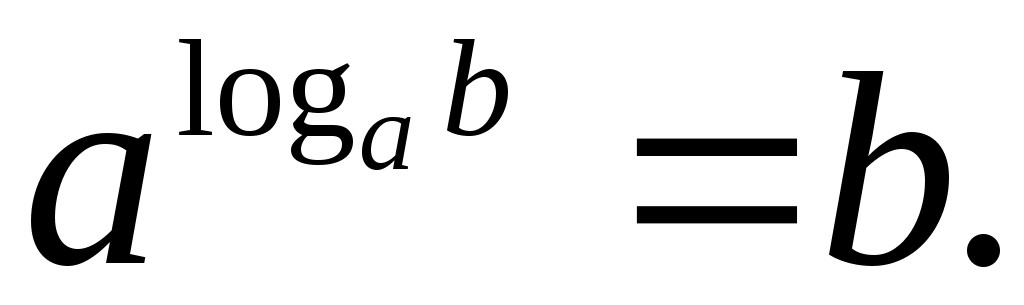
|
В первом случае число n становится показателем степени, стоящей в аргументе. Число n может быть абсолютно любым, ведь это просто значение логарифма
|
Вторая формула — это фактически перефразированное определение. Она так и называется: основное логарифмическое тождество
|
Задача
Найдите значение выражения: 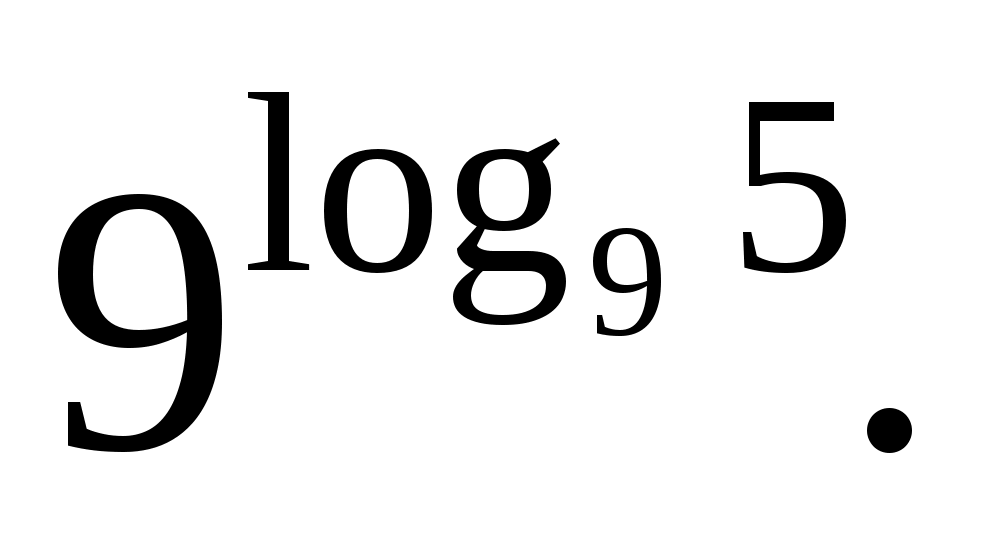
Решение:
Применяя основное логарифмическое тождество, получаем:
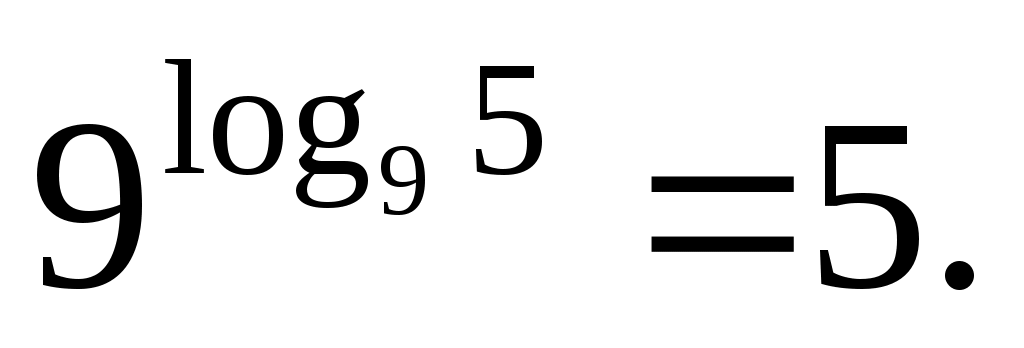
Ответ:
|
Задача
Найдите значение выражения: 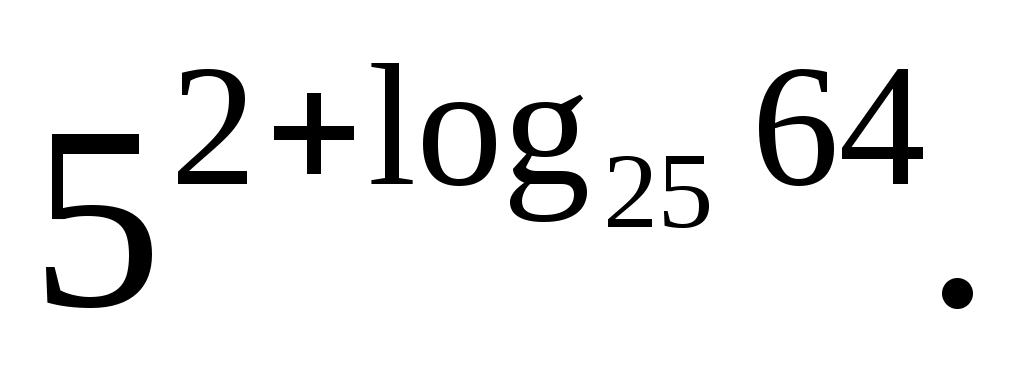
Решение:
Заметим, что 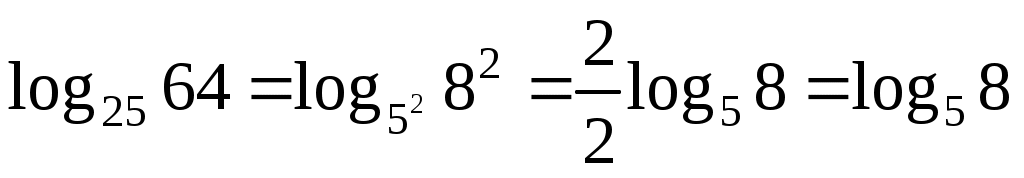 — просто вынесли квадрат из основания и аргумента логарифма. Учитывая правила умножения степеней с одинаковым основанием, получаем: — просто вынесли квадрат из основания и аргумента логарифма. Учитывая правила умножения степеней с одинаковым основанием, получаем:
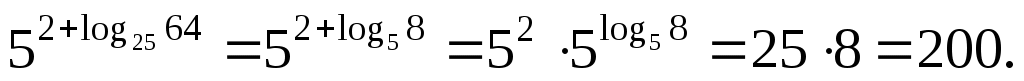
Ответ:
|
Историческая справка по теме.
«Зачем и где применяются логарифмы»
Знания логарифмов и основных логарифмических свойств необходимы для людей многих профессий: физиков, химиков, астрономов, психологов, географов и экологии.
Логарифмы по основанию 10 до изобретения калькуляторов широко применялись для вычислений. Неравномерная шкала десятичных логарифмов обычно наносится и на логарифмические линейки
Логарифмическая линейка хорошо знакома нашим родителям. Она позволяет выполнять умножение и деление чисел, возведение в степень и вычисление квадратных и кубических корней.
Шкала Рихтера - классификация силы землетрясений, созданная и представленная в 1935 г. геологом Чарльзом Рихтером. Шкала основана на принципе логарифма: каждое деление увеличивается в 10 раз, и его основанием является общая энергия, выделяемая при землетрясении.
В 1858 году немецкий физик и психолог Густав Фехнер доказал, основной психофизический закон, в котором говорится, что интенсивность воспринимаемого нами ощущения пропорциональна логарифму силы раздражения. Его формулируют так: «При изменении силы раздражителя в геометрической прогрессии, интенсивность ощущения меняется в арифметической прогрессии».
Логарифмы применяются и в психических явлениях. «Шкала Ландау» самый яркий пример. Знаменитый физик по ней оценивал заслуги своих коллег. Шкала была логарифмическая (классу 2 отвечали достижения в 10 раз меньше, чем для класса 1). Из физиков имел класс 0,5, Бор, Дирак, Гейзенберг имели класс 1
Астрономы измеряют «блеск» небесных светил в звездных величинах. Блеск в астрономии — величина пропорциональная логарифмусветового потока. Её направление обратное: чем больше значение звездной величины, тем слабее блеск объекта.
Химическая шкала кислотности очень близка к шкале звездных величин. Чем выше кислотность, тем ниже значение индекса, основанием логарифма служит число 10.
Играя на рояле, пианист играет на логарифмах. Ступени темперированной хроматической гаммы представляют логарифмы этих величин с основанием
Логарифмическая спираль часто встречается в природе. Впервые логарифмическая спираль описана Декартом, а потом была исследована Бернулли.
Паук Эпейра сплетая паутину, закручивает паутину, скручивая нити вокруг центра по логарифмической спирали.
Живые существа обычно растут во всех направлениях, сохраняя общее начертание своей формы. Раковины морских животных могут расти лишь в одном направлении. Чтобы не слишком вытягиваться в длину им приходится скручиваться.
Многие Галактики закручены по логарифмической спирали. Солнечная система, как одна из Галактик тоже закручена по такой спирали.
|
|
|
 Скачать 438.5 Kb.
Скачать 438.5 Kb.