АиГ. Ответы на экзамены
 Скачать 374.92 Kb. Скачать 374.92 Kb.
|
|
Ответы на экзамены: Множества и операции над ними. Множество – совокупность объектов выделяемых нами по каким-то признакам. (X) Элемент множества – объекты составляющие множество. (x) xX Отношение включения: Множество А содержится в множестве В, если каждый эл-т множества А является и элементом множества В. АВ Два множества называются равными (А=В), если выполняются 2 включения: АВ, ВА Подмножество множества А – любое множество содержащееся в А. АА В называется собственным подмножество А, если В содержится в А. Если В≠А, В – несобственное подмножество А. Операции над множествами: - Объединение множеств – такое множество, которое состоит из всех элементов, по крайней мере принадлежащих одному из множеств А и В. А В - Пересечение множеств – множество состоящее из элементов, принадлежащих и множ. А и множ. В. АВ - Пустое множество – если множество не содержит ни одного элемента. - Непересекающиеся множества – если их пересечение пустое множество. - Разность 2х множеств – множеств состоящее из эл-тов А, но не приналежащее множеству В. А\В - Дополнением к множеству А называется множество состоящее из элементов, не принадлежащих можеству А. СА - Произведением множеств Х и Y называется множество из упорядоченных пар (x,y), где х€Х, у€ Y. XY, XY≠ YX Свойства: 1) ССА=А 2) АВ= В А АВ= ВА 3) А(ВC)= (АВ)C А (ВC)= (АВ) C 4) А(ВC)= (АВ)(АC) А (ВC)= (АВ)(АC) Множества: N – множество натуральных чисел N={1, 2, 3…} Z – множество целых чисел {0, +-1,+-2…} R – множество действительных(вещественных) чисел NZR Отображения и их виды. Теорема о композиции отображений. Отображения Если между X и Y соответствие и элемент x сопоставляется y(x€X–>y€Y), то говорят, что задана ф-ция f, зависимости Х и Y(f:X–>Y или y=f(x)) f:X–>Y - сюръективное, если Yf=Y (f: отображ. множество Х на все множество Y) - инъективное, если x1≠x2 => f(x1)≠f(x2) (разные элементы множества Х не могут одновременно сопоставляться с одним и тем же элементом Y) - биективное, если оно одновременно является сюръективным и инъективным. f:X–>Y; АX тогда образом А при отображении f, называется множество ВY такое, что для любого элемента b€И существует a€A такой, что f(a)=b. f(A) – образ множества А f:X–>Y; ВY тогда прообразом В при отображении f, называется множество АХ такое, что любой элемент а€А имеет значение b=f(a)€B f-1(B) – прообраз множества В Обратные отображения. Теорема об обратном отображении. Обратное отображение: Пусть дано биективное отображение f:X->Y. Тогда по определению биекции для каждого y€Y существует в точности один x€X, такой что f(x) = y. Таким образом построена функция y€Y->x€X. Эта функция называется обратной к F и обозначается F −1 Для отображения f:x→y существует обратные отображение f – биэктивно. Если для отображения f:x→y, g:y→x выполнено fg = ex, gf = ey одновременно, то они g наз-ся обратным отображением к f. Лемма: Если для отображение f:x→y, g:y→x выполнено fg = ex, то f – инъективно, а g – сюръективно. Док-во: x,x’€X, f(x)=f(x‘) – образы равны x=ex (x) = fg(x)=g(f(x))=g(f(x’))=ex(x’)=x’ → f-инъекция: 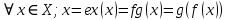 g-сюръективно g-сюръективноГеометрическое задание комплексных чисел. Плоскость комплексных чисел. Комплексные числа в алгебраической форме. Действия над ними. Алгебраическая форма комплексных чисел (рис. 5.1) Обозначения, терминология 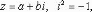 где i - мнимая единица; a - действительная часть: a = Re z; bi - мнимая часть: b = Im z; числа вида bi - чисто мнимые; плоскость Oxy - комплексная плоскость; ось Ох - действительная ось; ось Oy - мнимая ось;  - число, сопряженное числу z = a + bi; - число, сопряженное числу z = a + bi;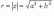 - модуль комплексного числа; - модуль комплексного числа; 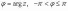 либо либо 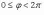 , - аргумент комплексного числа z (главное значение аргумента); , - аргумент комплексного числа z (главное значение аргумента);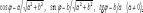 Arg z - множество аргументов числа z: 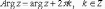  Действия над комплексными числами Если 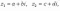 то: то: Геометрическая интерпретация комплексного числа. Тригонометрическая форма комплексного числа. Рассмотрим на плоскости декартову прямоугольную систему координат 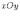 . Каждому комплексному числу . Каждому комплексному числу 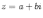 можно сопоставить точку с координатами можно сопоставить точку с координатами 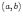 , и наоборот, каждой точке с координатами , и наоборот, каждой точке с координатами  можно сопоставить комплексное число можно сопоставить комплексное число 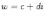 . Таким образом, между точками плоскости и множеством комплексных чисел устанавливается взаимно однозначное соответствие. Поэтому комплекные числа можно изображать как точки плоскости. Плоскость, на которой изображают комплексные числа, обычно называют комплексной плоскостью. . Таким образом, между точками плоскости и множеством комплексных чисел устанавливается взаимно однозначное соответствие. Поэтому комплекные числа можно изображать как точки плоскости. Плоскость, на которой изображают комплексные числа, обычно называют комплексной плоскостью. Пример 17.3 Изобразим на комплексной плоскости числа 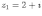 , ,  , , 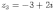 , ,  , , 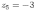 : : 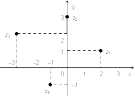 Рис.17.1.Изображение комплексных чисел точками плоскости Однако чаще комплексные числа изображают в виде вектора с началом в точке 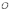 , а именно, комплексное число , а именно, комплексное число 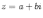 изображается радиус-вектором точки с координатами изображается радиус-вектором точки с координатами 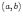 . В этом случае изображение комплексных чисел из предыдущего примера будет таким: . В этом случае изображение комплексных чисел из предыдущего примера будет таким: 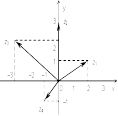 Рис.17.2.Изображение комплексных чисел векторами Отметим, что изображением суммы двух комплексных чисел  , ,  является вектор, равный сумме векторов, изображающих числа является вектор, равный сумме векторов, изображающих числа  и и  . Иными словами, при сложении комплексных чисел складываются и векторы, их изображающие (рис. 17.3). . Иными словами, при сложении комплексных чисел складываются и векторы, их изображающие (рис. 17.3). 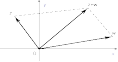 Рис.17.3.Изображение суммы комплексных чисел Сопряженные числа и их свойства. Тригонометрическая форма комплексного числа. Умножение и деление комплексных чисел в тригонометрической форме. Пусть 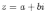 . Положим . Положим 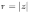 , , 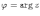 . Из рисунка 17.4 очевидно, что . Из рисунка 17.4 очевидно, что 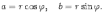 Тогда  . Это выражение запишем в виде . Это выражение запишем в виде 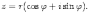 (17.8) (17.8)Последняя запись называется тригонометрической формой комплексного числа. В отличие от нее запись числа в виде 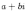 называют иногда алгебраической формой комплексного числа. называют иногда алгебраической формой комплексного числа. Отметим, что тригонометрическая форма -- это указание числа по двум его характеристикам: модулю и аргументу. Поэтому вместо формулы (17.8) можно было бы просто записывать пару 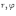 , но запись (17.8) принята в силу традиции. , но запись (17.8) принята в силу традиции. Формула Муавра. Формулы для синуса и косинуса кратного угла. Пусть  , ,  . Найдем произведение . Найдем произведение 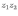 : :  Заметим, что во внутренних скобках стоят формулы косинуса и синуса суммы аргументов. Поэтому 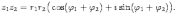 Последняя запись является тригонометрической формой комплексного числа 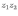 . Значит, . Значит, 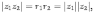 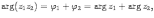 иными словами, при умножении комплексных чисел их модули перемножаются, а аргументы складываются. Аналогично можно доказать, что 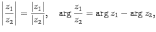 иными словами, при делении комплексных чисел их модули делятся один на другой, а аргументы вычитаются. Несложно проверить, что если 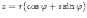 , то , то 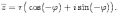 Используя правило умножения комплексных чисел в тригонометрической форме, получим формулу для возведения комплексного числа в степень  , где , где  -- натуральное число. -- натуральное число. Пусть 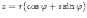 . Тогда . Тогда 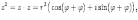 то есть 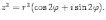 Далее находим 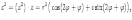 то есть  Продолжая умножения дальше, придем к формуле 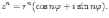 (17.9) (17.9)Эта формула называется формулой Муавра. Извлечение корня из комплексного числа. Определение. Корнем n-й степени из комплексного числа z (обозначают 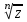 ) называется комплексное число w такое, что wn = z. Если z = 0, то ) называется комплексное число w такое, что wn = z. Если z = 0, то 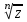 = 0. = 0.Пусть z 0, z = r(cos + isin). Обозначим w = (cos + sin), тогда уравнение wn = z запишем в cледующем виде n(cos(n·) + isin(n·)) = r(cos + isin). Отсюда n = r, n· = + 2k, k Z. Далее 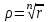 , , = 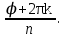  Таким образом, wk = 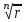 · ·  . .Среди этих значений ровно n различных. Поэтому k = 0, 1, 2, …, n – 1. На комплексной плоскос-ти эти точки являются вершинами правильного n-угольника, вписан-ного в окружность радиусом 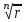 с центром в точке О. с центром в точке О.Извлечение корня n-й степени из единицы. 1 = cos0+i sin0 Корни расположены на окружности единичного радиуса и делят эту окружность на n равных частей. Теорема 1.Все значения корня n–той степени из комплексного числа z можно получить умножением одного из них на все корни из 1. Доказательство: Возьмём = 1, 2,…, n – так обозначим все корни Домножим каждый из корней 1,…, n на . Они разные, все являются корнями n–той степени из z, ибо (i)n = z и их Теорема доказана. Теорема 2. Произведение двух корней n–той степени из единицы есть корень степени n из единицы. Следствие. Степень корня n–той степени из единицы есть корень степени n из единицы. Все ли корни из 1 равноправны? n=4 ; 1, –1, i, –i — корни из единицы. i; –i — первообразные корни; если i возводить в степени 0, 1, 2, 3, то получим все корни. Определение 1. Корень n–той степени из 1 называется первообразным, если он не даёт единицу в степени меньше, чем n. Показательная форма комплексного числа. Действия над комплексными числами в показательной форме. Показательная и тригонометрические функции в области комплексных чисел связаны между собой формулой 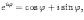 (17.10) (17.10)которая носит название формулы Эйлера. Обосновать ее можно с помощью теории степенных рядов. Эта теория будет изложена в курсе математического анализа. Пусть комплексное число  в тригонометрической форме имеет вид в тригонометрической форме имеет вид 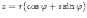 . На основании формулы Эйлера выражение в скобках можно заменить на показательное выражение. В результате получим . На основании формулы Эйлера выражение в скобках можно заменить на показательное выражение. В результате получим 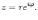 Эта запись называется показательной формой комплексного числа. Так же, как и в тригонометрической форме, здесь 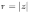 , , 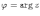 . .  13. Операции над многочленами и их свойства. |
