Ответы на вопросы по информатике Форма представления текстовых и числовых данных в компьютере

• Название: Ответы на вопросы по информатике Форма представления текстовых и числовых данных в компьютере
• Дата: 19.01.2022
• Размер: 1.05 Mb.
• Имя файла: Otvety_na_voprosy_po_informatike.docx
• Тип: Документы; #335794
• страница: 3 из 4

19.Примеры использования статистических функций

Формулы функций в Excel можно вводить вручную непосредственно в той ячейке, где планируется выполнить соответствующие расчеты. Это легко применимо к таким простым действиям, как сложение, вычитание, умножение и деление. Но запомнить формулы сложных функций уже непросто, поэтому проще воспользоваться специальным помощником, который встроен в программу.

Итак, чтобы вставить функцию в ячейку, выполняем одно из следующих действий:

1. Находясь в любой вкладке программы щелкаем по значку “Вставить функцию” (fx), которая находится с левой стороны от строки формул.

2. Переходим во вкладку “Формулы”, где видим в левом углу ленты инструментов кнопку “Вставить функцию”.

3. Используем сочетание клавиш Shift+F3.

4. Независимо от выбранного способа выше перед нами появится окно вставки функций. Щелкаем по текущей категории и из раскрывшегося списка выбираем пункт “Статистические”.

5. Далее будет предложен на выбор один из статистических операторов. Отмечаем нужный и жмем OK.

6. На экране отобразится окно с аргументами выбранной функции, которые нужно заполнить.

СРЗНАЧ

Оператор вычисляет среднее арифметическое значение из указанных значений (диапазона). Формула функции выглядит таким образом:

=СРЗНАЧ(число1;число2;…)

МАКС

Функция помогает определить максимальное значение из заданных чисел (диапазона). Формула оператора следующая:

=МАКС(число1;число2;…)

В аргументах функции, также, как и в случае с оператором СРЗНАЧ можно указать конкретные числа, ссылки на ячейки или диапазоны ячеек.

МИН

Функция находит минимальное число из указанных значений (диапазона ячеек). В общем виде синтаксис выглядит так:

=МИН(число1;число2;…)

Аргументы функции заполняются так же, как и для оператора МАКС.

СРЗНАЧЕСЛИ

Функция позволяет найти среднее арифметическое значение, но при выполнении заданного условия. Формула оператора:

=СРЗНАЧЕСЛИ(диапазон;условие;диапазон_усреднения)

В аргументах указываются:

· Диапазон ячеек – вручную или с помощью выделения в таблице;

· Условие отбора значений из заданного диапазона (больше, меньше, не равно) – в кавычках;

· Диапазон_усреднения – не является обязательным аргументом для заполнения.

МЕДИАНА

Оператор находит медиану заданного диапазона значений. Синтаксис функции:

=МЕДИАНА(число1;число2;…)

В аргументах указываются: конкретные числа, ссылки на ячейки или диапазоны элементов.

НАИБОЛЬШИЙ

Функция позволяет найти из указанного диапазона значений с заданной позицией (по убыванию). Формула оператора:

=НАИБОЛЬШИЙ(массив;k)

Аргумента функции два: массив и номер позиции – K.

НАИМЕНЬШИЙ

Функция также, как и оператор НАИБОЛЬШИЙ, выполняет поиск из указанного диапазона значений. Правда, в данном случае счет идет по возрастанию. Синтаксис оператора следующий:

=НАИМЕНЬШИЙ(массив;k)

МОДА.ОДН

Функция пришла на замену более старому оператору “МОДА” (теперь находится в категории “Полный алфавитный перечень”). Позволяет определять число, которое повторяется чаще остальных в выбранном диапазоне. Работает функция по формуле:

=МОДА.ОДН(число1;число2;…)

В значениях аргументов указываются конкретные числовые значения, отдельные ячейки или их диапазоны.

20. Примеры использования логических функций

Логическая функция — это такая функция, которая может принимать только одно из 2-х значений: 0 («ложь», «false») или 1 («истина», «true»).

Существует несколько операторов логических функций. Среди основных следует выделить такие:

· ИСТИНА;

· ЛОЖЬ;

· ЕСЛИ;

· ЕСЛИОШИБКА;

· ИЛИ;

· И;

· НЕ;

· ЕОШИБКА;

· ЕПУСТО.

Использование

Логические функции используют для проверки и анализа данных, а также в условных вычислениях. Логические функции в качестве аргументов используют логические выражения. Логические выражения используются для записи условий, в которых сравниваются числовые или текстовые значения.

Пример

Перед человеком поставлена цель осуществить переоценку товарных остатков. В случае хранения продукта в течение большего, чем 8 месяцев периода, необходимо снижать его стоимость в два раза. Изначально нужно сформировать такую таблицу.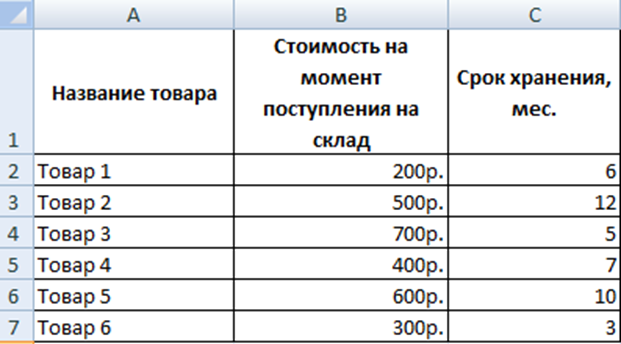



Для достижения поставленной цели необходимо использовать функцию ЕСЛИ. В случае с нашим примером будет так выглядеть эта формула: =ЕСЛИ(C2>=8;B2/2;B2)

Логическое выражение, содержащееся в первом аргументе функции, составлено с использованием операторов > и =. Простыми словами, изначально критерий следующий: при значении ячейки, большем или равном 8, выполняется формула, поставленная во втором аргументе. Выражаясь терминологическим языком, если первое условие оказывается истинным, то выполняется второй аргумент. Если же ложным – третий.

21. Типы диаграмм и графиков, способы их построения.

Диаграммы-линии или графики — это тип диаграмм, на которых полученные данные изображаются в виде точек, соединённых линиями. Точки могут быть как видимыми, так и невидимыми (ломаные линии). Также могут изображаться точки без линий (точечные диаграммы). Для построения диаграмм-линий применяют прямоугольную систему координат. Обычно по оси абсцисс откладывается время (годы, месяцы и т. д.), а по оси ординат — размеры изображаемых явлений или процессов. На осях наносят масштабы.

Диаграммы-линии целесообразно применять тогда, когда число размеров (уровней) в ряду велико. Кроме того, такие диаграммы удобно использовать, если требуется изобразить характер или общую тенденцию развития явления или явлений. Линии удобны и при изображении нескольких динамических рядов для их сравнения, когда требуется сравнение темпов роста. На одной диаграмме такого типа не рекомендуется помещать более трёх-четырёх кривых. Их большое количество может усложнить чертёж, и линейная диаграмма может потерять наглядность. Основной недостаток диаграмм-линий — равномерная шкала, позволяющая измерить и сравнить только абсолютные приросты или уменьшения показателей в течение периода исследований. Относительные изменения показателей искажаются при изображении их с равномерной вертикальной шкалой. Также в такой диаграмме может быть невозможным изображение рядов динамики с резкими скачками уровней, которые требуют уменьшения масштаба диаграммы, и показатели в ней динамики более «спокойного» объекта теряют свою точность. Вероятность присутствия в этих типах диаграмм резких изменений показателей возрастает с увеличением длительности периода времён на графике.

Диаграммы-области — это тип диаграмм, схожий с линейными диаграммами способом построения кривых линий. Отличается от них тем, что область под каждым графиком заполняется индивидуальным цветом или оттенком. Преимущество данного метода в том, что он позволяет оценивать вклад каждого элемента в рассматриваемый процесс. Недостаток это типа диаграмм также схож с недостатком обычных линейных диаграмм — искажение относительных изменений показателей динамики с равномерной шкалой ординат.

Построение столбчатой диаграммы заключается в изображении статистических данных в виде вертикальных прямоугольников или трёхмерных прямоугольных столбиков. Каждый столбик изображает величину уровня данного статистического ряда. Все сравниваемые показатели выражены одной единицей измерения, поэтому удаётся сравнить статистические показатели данного процесса.

Разновидностями столбчатых диаграмм являются полосовые диаграммы. Они отличаются горизонтальным расположением столбиков. Столбчатые и полосовые диаграммы взаимозаменяемы, рассматриваемые в них статистические показатели могут быть представлены как вертикальными, так и горизонтальными столбиками. В обоих случаях для изображения величины явления используется одно измерение каждого прямоугольника — высота или длина столбика. Поэтому и сфера применения этих двух диаграмм в основном одинакова.

Столбчатые диаграммы могут изображаться и группами (одновременно расположенными на одной горизонтальной оси с разной размерностью варьирующих признаков). Образующие поверхности столбчатых и полосовых диаграмм могут представлять собой не только прямоугольники, но также квадраты, треугольники, трапеции и т. д.

Круговые (секторные) диаграммы

Достаточно распространённым способом графического изображения структуры статистических совокупностей является секторная диаграмма, так как идея целого очень наглядно выражается кругом, который представляет всю совокупность. Относительная величина каждого значения изображается в виде сектора круга, площадь которого соответствует вкладу этого значения в сумму значений.

Радиальные (сетчатые) диаграммы

В отличие от линейных диаграмм, в радиальных или сетчатых диаграммах более двух осей. По каждой из них производится отсчёт от начала координат,

находящегося в центре. Для каждого типа полученных значений создаётся своя собственная ось, которая исходит из центра диаграммы. Радиальные диаграммы напоминают сетку или паутину, поэтому иногда их называют сетчатыми. Преимущество радиальных диаграмм в том, что они позволяют отображать одновременно несколько независимых величин, которые характеризуют общее состояние структуры статистических совокупностей. Если отсчёт производить не с центра круга, а с окружности, то такая диаграмма будет называться спиральной диаграммой. Картодиаграммы — это сочетания диаграмм с географическими картами или схемами. В качестве изобразительных знаков в картодиаграммах используются обычные диаграммы (гистограммы, круговые, линейные), которые размещаются на контурах географических карт или на схемах каких-либо объектов. Картодиаграммы дают возможность географически отразить более сложные статистико-географические построения, чем обычные типы диаграмм.

Недостатком картодиаграмм могут служить сложности в рисовании контуров карт, а также значительная разница в размерах областей географических карт и размеров диаграмм на них.

Биржевые диаграммы отражают наборы данных из нескольких значений (например: цена открытия биржи, цена закрытия, максимальная и минимальная цена определённого временного интервала). Применяются для отображения биржевых данных: котировок акций или валют, данных спроса и предложения.

22. Сортировка данных и способы ее осуществления (одноуровневая, многоуровневая).

Списки можно сортировать, чтобы изменить порядок следования записей. Сортировка может осуществляться по отдельным полям (одноуровневая сортировка), а при равенстве значений в полях — по другим полям (многоуровневая сортировка).

Одноуровневая сортировка

Для быстрой сортировки по отдельному полю следует выделить любую ячейку в столбце, по которому будет проводиться сортировка и на вкладке Данные в группе Сортировка и фильтр выполните одно из указанных ниже действий.

· Чтобы отсортировать значения по алфавиту в порядке возрастания, нажмите кнопку Сортировка от А до Я.

· Чтобы отсортировать значения по алфавиту в порядке убывания, нажмите кнопку Сортировка от Я до А.

Многоуровневая сортировка

Сортировку можно осуществлять по нескольким столбцам или строкам, чтобы сгруппировать данные с одинаковыми значениями в одном столбце или строке, а затем выполнить сортировку другого столбца или строки в этих группах с одинаковыми значениями.

Для многоуровневой сортировки необходимы следующие действия.

1. Выделите диапазон ячеек с двумя или более столбцами данных или убедитесь в том, что активная ячейка находится в таблице с двумя или более столбцами.

2. На вкладке Данные в группе Сортировка и фильтр нажмите кнопку Сортировка. Появится диалоговое окно Сортировка.

3. В группе Столбец в поле Сортировать по выберите первый столбец, который необходимо отсортировать.

4. В поле Сортировка выберите тип сортировки. Выполните одно из указанных ниже действий.

· Для сортировки по текстовым, числовым значениям или значениям даты и времени выберите пункт Значения.

· Для сортировки по типам форматирования выберите пункт Цвет ячейки, Цвет шрифта или Значок ячейки.

5. В группе Порядок выберите последовательность, в которой необходимо осуществлять сортировку. Выполните одно из указанных ниже действий.

· Для текстовых значений выберите пункт От А до Я или От Я до А.

· Для числовых значений выберите пункт По возрастанию или По убыванию.

· Для сортировки по датам и времени выберите пункт От старых к новым или От новых к старым.

· Для сортировки на основе настраиваемых списков выберите пункт Настраиваемый список.

6. Для добавления к сортировке следующего столбца нажмите кнопку Добавить уровень, а затем повторите шаги с третьего по пятый.

7. Чтобы изменить порядок сортировки столбцов, выделите запись нужного столбца и щелкните стрелку Вверх или Вниз.

23.Фильтры и их виды.

Фильтры- средство поиска данных, которое применяют для сужения списка с целью исключения из него (на время) ненужной информации

Фильтрация — это быстрый способ выделения из списка подмножества данных для последующей работы с ними.

Excel содержит два варианта фильтрации: автофильтр и усиленный фильтр.

Автофильтр осуществляет быструю фильтрацию списка в соответствии с содержимым ячеек или в соответствии с простым критерием поиска. Активизация автофильтра осуществляется командой Фильтр — Автофильтр меню Данные (указатель должен быть установлен внутри области списка). Заглавная строка списка в режиме автофильтра содержит в каждом столбце кнопку со стрелкой. Щелчок раскрывает списки, элементы которого участвуют в формировании критерия. Каждое поле (столбец) может использоваться в качестве критерия.

Расширенный фильтр предназначен для фильтрации списка в соответствии с заданными пользовательскими критериями. В отличие от автофильтра критерии расширенного фильтра формируются и располагаются в области рабочего листа. Преимуществами этого способа являются:

· возможность сохранения критериев и их многократного использования;

· возможность оперативного внесения изменений в критерии в соответствии с потребностями;

· возможность располагать результаты фильтрации в любой области рабочего листа.

Фильтрация списка с помощью усиленного фильтра выполняется командой Фильтр — Расширенный фильтр меню Данные. В окне команды Расширенный фильтр следует указать:

1) в поле ввода Исходный диапазон — диапазон ячеек, содержащих список; 2) в поле ввода Диапазон условий — диапазон ячеек, содержащих критерий отбора;

3) в поле ввода Поместить результат в диапазон — верхнюю левую ячейку области, начиная с которой будет выведен результат фильтрации;

4) с помощью переключателя Обработка определить расположение результатов фильтрации на рабочем листе:

o Фильтровать список на месте — означает, что список остается на месте, ненужные строки скрываются;

o Скопировать результаты в другое место — позволяет расположить результаты фильтрации в другой области рабочего листа.

5) Параметр Только уникальные записи — означает, что выборка должна содержать только уникальные записи в соответствии с критериями отбора.

24. Сущность сводных таблиц и способы их создания.

Сводные таблицы предназначены для удобного просмотра данных больших таблиц, т.к. обычными средствами делать это неудобно, а порой, практически невозможно.

Сводными называются таблицы, содержащие часть данных анализируемой таблицы, показанные так, чтобы связи между ними отображались наглядно. Сводная таблица создается на основе отформатированного списка значений. Поэтому, прежде чем создавать сводную таблицу, необходимо подготовить соответствующим образом данные.

При недостатке опыта работы со сводными таблицами или отсутствии знаний о них лучше воспользоваться автоматическими сводными таблицами. При использовании этой функции Excel определяет подходящий макет, сопоставляя данные с наиболее подходящими областями в сводной таблице. После создания базовой сводной таблицы и визуализации ее компонентов следует изучить различные ориентации и изменить порядок полей для получения нужных результатов.

1. Откройте книгу, в которой требуется создать сводную таблицу.

2. Щелкните ячейку в списке или таблице, которые содержат нужные данные.

3. На вкладке Данные в разделе Анализ нажмите кнопку Сводная таблица.

Excel создаст на новом листе сводную таблицу и отобразит конструктор сводных таблиц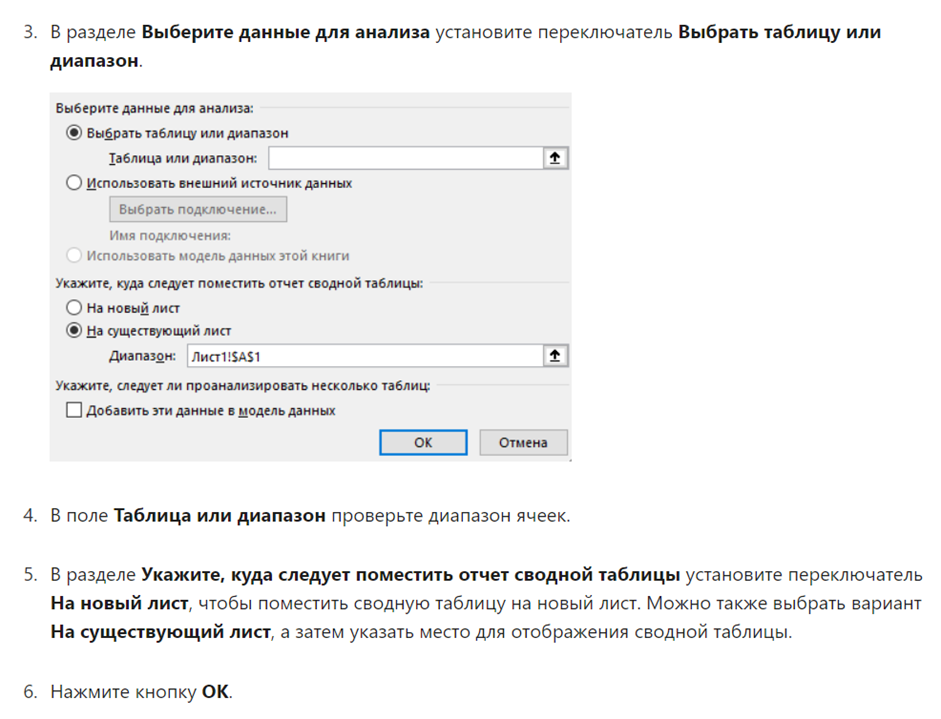





25.Назначение метода Подбор параметра.

Подбор параметра – способ поиска определенного значения ячейки путем изменения значения в другой ячейке. При подборе параметра приложение изменяет значение в одной конкретной в ячейке до тех пор, пока формула, зависящая от этой ячейки, не вернет требуемый результат. Команда Подбор параметра находит только одно решение, даже если задача имеет несколько решений, и только для одной ячейки. Перед применением рассматриваемого инструмента следует решить задачу средствами электронных таблиц с любыми исходными данными.

26.1)Назначение метода 2)Поиск решения.

· 1)Ме́тод в объектно-ориентированном программировании — это функция или процедура, принадлежащая какому-то классу или объекту. Как и процедура в процедурном программировании, метод состоит из некоторого количества операторов для выполнения какого-то действия и имеет набор входных аргументов.

Различают простые методы и статические методы (методы класса):

· простые методы имеют доступ к данным объекта (конкретного экземпляра данного класса),

· статические методы не имеют доступа к данным объекта, и для их использования не нужно создавать экземпляры (данного класса).

В зависимости от того, какой уровень доступа предоставляет тот или иной метод, выделяют:

· открытый (public) интерфейс — общий интерфейс для всех пользователей данного класса;

· защищённый (protected) интерфейс — внутренний интерфейс для всех наследников данного класса;

· закрытый (private) интерфейс — интерфейс, доступный только изнутри данного класса.

· 2)«Поиск решений» — функция Excel, которую используют для оптимизации параметров: прибыли, плана продаж, схемы доставки грузов, маркетингового бюджета или рентабельности. Она помогает составить расписание сотрудников, распределить расходы в бизнес-плане или инвестиционные вложения. Знание этой функции экономит много времени и сил. Рассказываем, как освоить функцию поиска решений.

Основные параметры поиска решений

Найти решение задачи можно тремя способами. Во-первых, вручную перебирать параметры, пока не найдется оптимальное соотношение. Во-вторых, составить уравнение с большим количеством неизвестных. В-третьих, вбить данные в Excel и использовать «Поиск решений». Последний способ самый быстрый и покажет максимально точное решение, если знать, как использовать функцию.

Итак, мы решаем задачу с помощью поиска решений в Excel и начинаем с математической модели. В ней четыре типа данных: константы, изменяемые ячейки, целевая функция и ограничения. К поиску решения вернемся чуть позже, а сейчас разберемся, что входит в каждый из этих типов: