Перебор последовательности целых чисел. Проверка делимости

• Название: Перебор последовательности целых чисел. Проверка делимости
• Дата: 26.09.2022
• Размер: 0.86 Mb.
• Имя файла: ege17.doc
• Тип: Документы; #698851
• страница: 1 из 10

© К. Поляков, 2018-2022

17 (повышенный уровень, время – 14 мин)

Тема: Перебор последовательности целых чисел. Проверка делимости

Что проверяется:

Умение создавать собственные программы (20–40 строк) для обработки целочисленной информации.

1.7.2. Основные конструкции языка программирования. Система программирования.

1.1.5. Умение создавать программы на языке программирования по их описанию.

Что нужно знать:

• 
  в известных задачах этого типа (не олимпиадных) нет ограничения на время выполнения, по крайней мере, оно несущественно для отрезков, заданных для перебора; поэтому можно использовать простой перебор без оптимизации;
  
• 
  задачи этого типа предлагается решать с помощью электронных таблиц или собственной программы; как правило, написать правильную программу значительно проще
  
• 
  пусть необходимо перебрать все целые числа на отрезке [a; b] и подсчитать, для скольких из них выполняется некоторое условие; общая структура цикла перебора записывается так (Python):
  

count = 0

for n in range(a, b+1):

if условие выполнено:

count += 1

print( count )

Pascal:

count := 0;

for n:=a to b do

if условие выполнено then

count := count + 1;

writeln(count);

C++:

int count = 0;

for(int n = a; n <= b; n++)

if( условие выполнено )

count += 1;

std::cout << count;

• 
  проверку условия удобно оформить в виде функции, возвращающей логическое значение (True/False), но можно этого и не делать
  
• 
  проверить делимость числа n на число d можно с помощью операции взятия остатка от деления n на d: если остаток равен 0, число n делится на d нацело
  
• 
  проверка на языке Python выглядит так:
  

if n % d == 0:

print("Делится")

else: print("Не делится")

• 
  тоже самое на Pascal
  

if n mod d = 0 then

writeln('Делится')

else writeln('Не делится')

• 
  то же самое на C++
  

if( n % d == 0 )

std::cout << "Делится";

else std::cout << "Не делится";

Пример задания:

Р-01 (демо-2021). Рассматривается множество целых чисел, принадлежащих числовому отрезку [1016; 7937], которые делятся на 3 и не делятся на 7, 17, 19, 27. Найдите количество таких чисел и максимальное из них. В ответе запишите два целых числа: сначала количество, затем максимальное число. Для выполнения этого задания можно написать программу или воспользоваться редактором электронных таблиц.

Решение (электронные таблицы Excel):

1. 
   введём начальное число в ячейку A1: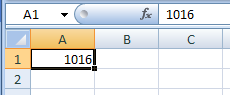
   

2. 
   заполним ряд натуральных чисел до конечного числа; на вкладке Главная выберем команду Прогрессия: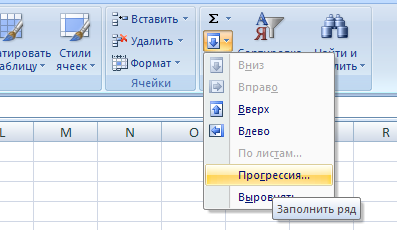
   

3. 
   введём шаг и конечное значение, заполнение по столбцам: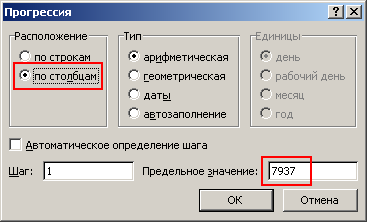
   

4. 
   в столбце определим логическое значение: истина, если остаток от деления числа в столбце A делится на 3: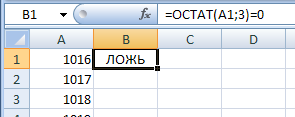
   

5. 
   двойным щелчком по маркеру заполнения скопируем формулу на весь столбец (пока не кончатся данные в столбце A)
   
6. 
   в столбце C выведем ИСТИНА, если соответствующее значение в столбце А не делится на 7: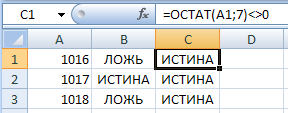
   

(Б.С. Михлин) Можно записать формулу чуть короче: =ОСТАТ(А1;7), т.к. численное значение, отличное от нуля рассматривается как ИСТИНА

7. 
   в столбцах D, E, F аналогично выведем ИСТИНА, если соответствующее значение в столбце А не делится на 17, 19 и 27: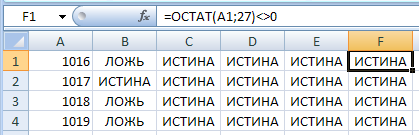
   

(Б.С. Михлин) аналогично п.6, «<>0» в формулах можно не писать.

8. 
   в столбце G используем функцию ЕСЛИ; если все значения ячеек в столбцах B-F в этой строке истинны, выводим число из А1, иначе – пустую строку: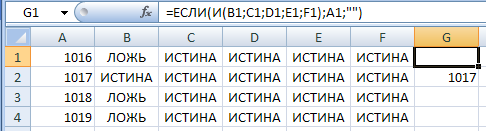
   

(Б.С. Михлин) Можно написать формулу чуть короче, используя диапазон в команде И: =ЕСЛИ(И(B1:F1);A1;"")

9. 
   теперь в столбце G мы видим только те числа, которые удовлетворяют условию задачи; прокрутив таблицу вниз, узнаем, что последняя строка имеет номер 6922, поэтому находим количество и максимум для диапазона G1:G6922 в любых свободных ячейках:
   

=СЧЁТ(G1:G6922)

=МАКС(G1:G6922) (это последнее число в столбце G)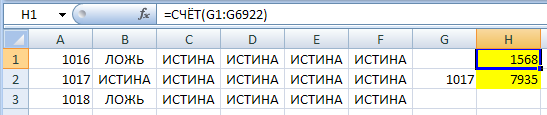

10. 
    Ответ: 1568 7935
    
11. 
    (И.В. Степанов) чтобы уменьшить таблицу в 3 раза, можно проверять только числа, кратные 3, с шагом 3; первое число на заданном отрезке, кратное 3 – это 1017 (сумма цифр делится на 3).
    

Решение (электронные таблицы LibreOffice Calc):

1. 
   введём начальное значение диапазона в ячейку A1
   
2. 
   подсчитаем количество чисел в диапазоне: 7937 – 1016 + 1 = 6922
   
3. 
   выделим диапазон A1:A6922, для этого введём его адрес в левом верхнем углу таблицы: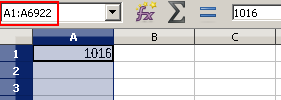
   

4. 
   заполним диапазон арифметической прогрессией, используя команду верхнего меню Правка – Заполнить – Ряды (в последних версиях Лист – Заполнить – Ряды):
   
5. 
   далее последовательность действий такая же, как при использовании Excel
   
6. 
   Ответ: 1568 7935
   

Решение (электронные таблицы OpenOffice Calc):

1. 
   последовательность действий такая же, как для LibreOffice Calc, но нужно использовать английские названия функций (слева записаны адреса ячеек, в которые эти формулы заносятся):
   

B1: =MOD(A1;3)=0

C1: =MOD(A1;7)<>0

D1: =MOD(A1;17)<>0

E1: =MOD(A1;19)<>0

F1: =MOD(A1;27)<>0

G1: =IF(AND(B1;C1;D1;E1;F1);A1;"")

H1: =COUNT(G1:G6922)

H2: =MAX(G1:G6922)

2. 
   Ответ: 1568 7935
   

Решение (простой перебор):

1. 
   поскольку заданный отрезок [1016; 7937] содержит не так много чисел, можно решать задачу простым перебором, особо не заботясь об эффективности вычислений
   
2. 
   условие будем понимать так: интересующие нас числа делятся на 3 и не делятся ни на одно из чисел 7, 17, 19 и 27
   
3. 
   нам выгоднее перебирать числа в порядке возрастания, тогда последнее найдённое число – это и есть искомое максимальное подходящее число (если требуется найти наименьшее подходящее число, удобнее перебирать числа в порядке убывания)
   
4. 
   полная программа на языке Python:
   

count = 0

maxGood = 0

for n in range(1016, 7937+1):

if (n % 3 == 0) and (n % 7 != 0) and \

(n % 17 != 0) and (n % 19 != 0) and (n % 27 != 0):

maxGood = n

count += 1

print(count, maxGood)

5. 
   ещё один вариант программы (с функцией):
   

def isGood(n):

return (n % 3 == 0) and (n % 7 != 0) and \

(n % 17 != 0) and (n % 19 != 0) and (n % 27 != 0)

count = 0

maxGood = 0

for n in range(1016, 7937+1):

if isGood(n):

maxGood = n

count += 1

print(count, maxGood)

6. 
   (Б.С. Михлин) на языке Python существует короткое решение, использующее генератор списка:
   

# В списке (массиве) "a" только нужные числа:

a = [n for n in range(1016,7937+1)

if (n%3==0 and n%7!=0 and n%17!=0 and

n%19!=0 and n%27!=0)]

print(len(a),max(a)) # max(a) можно заменить на a[-1]

# (последний элемент списка "a")

Используя идею И.В. Степанова (см. далее) и то, что числа отличные от нуля рассматриваются, как истина (True), можно программу написать еще короче:

a = [n for n in range(1017,7937+1,3)

if n%7 and n%17 and n%19 and n%27]

print(len(a),a[-1])

7. 
   Ответ: 1568 7935
   
8. 
   (И.В. Степанов) чтобы ускорить перебор в 3 раза можно проходить только числа, кратные 3, в цикле с шагом 3; первое число на заданном отрезке, кратное 3 – это 1017 (сумма цифр делится на 3), поэтому на Python получаем такую программу:
   

count = 0

maxGood = 0

for n in range(1017, 7937+1, 3):

if (n % 3 == 0) and (n % 7 != 0) and \

(n % 17 != 0) and (n % 19 != 0) and (n % 27 != 0):

maxGood = n

count += 1

print(count, maxGood)

очевидно, что проверку делимости на 3 делать уже не нужно.

Решение (программа на языке Pascal):

1. 
   аналогичная программа на языке Pascal:
   

var count, n, maxGood: integer;

begin

count:= 0;

maxGood:= 0;

for n:=1016 to 7937 do

if (n mod 3 = 0) and (n mod 7 <> 0) and

(n mod 17 <> 0) and (n mod 19 <> 0) and

(n mod 27 <> 0) then begin

maxGood:= n;

count := count + 1

end;

writeln(count, ' ', maxGood)

end.

2. 
   вариант с функцией:
   

var count, n, maxGood: integer;

function isGood(n: integer): boolean;

begin

isGood := (n mod 3 = 0) and (n mod 7 <> 0) and

(n mod 17 <> 0) and (n mod 19 <> 0) and

(n mod 27 <> 0);

end;

begin

count:= 0;

maxGood:= 0;

for n:=1016 to 7937 do

if isGood(n) then begin

maxGood:= n;

count:= count + 1

end;

writeln(count, ' ', maxGood)

end.

3. 
   Ответ: 1568 7935
   

Решение (программа на языке PascalABC.NET, А. Богданов):

1. 
   следующая программа получилась очень короткой, однако она использует некоторые нетривиальные возможности современных версий PascalABC.NET, например, лямбда-функцию и методы Where, DivsAny (версия 3.7.1+):
   

begin

var s := Range( 1017, 7937, 3)

.Where( i -> not i.DivsAny(7, 17, 19, 27) );

print( s.Count, s.Max );

end.

2. 
   Ответ: 1568 7935
   

Решение (программа на языке C++):

3. 
   аналогичная программа на языке C++:
   

#include

int main()

{

int count = 0;

int maxGood = 0;

for(int n=1016; n<=7937; n++)

if( (n % 3 == 0) and (n % 7 != 0) and

(n % 17 != 0) and (n % 19 != 0) and (n % 27 != 0) ) {

maxGood = n;

count += 1;

}

std::cout << count << " " << maxGood;

}

4. 
   ускоренный перебор (с шагом 3):
   

#include

int main()

{

int count = 0;

int maxGood = 0;

for(int n=1017; n<=7937; n+=3)

if( (n % 3 == 0) and (n % 7 != 0) and

(n % 17 != 0) and (n % 19 != 0) and (n % 27 != 0) ) {

maxGood = n;

count += 1;

}

std::cout << count << " " << maxGood;

}

5. 
   вариант с функцией:
   

#include

bool isGood( int n )

{

return (n % 3 == 0) and (n % 7 != 0) and

(n % 17 != 0) and (n % 19 != 0) and (n % 27 != 0);

}

int main()

{

int count = 0;

int maxGood = 0;

for(int n=1016; n<=7937; n++)

if( isGood(n) ) {

maxGood = n;

count += 1;

}

std::cout << count << " " << maxGood;

}

6. 
   ускоренный перебор (с функцией):
   

#include

bool isGood( int n )

{

return (n % 3 == 0) and (n % 7 != 0) and

(n % 17 != 0) and (n % 19 != 0) and (n % 27 != 0);

}

int main()

{

int count = 0;

int maxGood = 0;

for(int n=1017; n<=7937; n+=3)

if( isGood(n) ) {

maxGood = n;

count += 1;

}

std::cout << count << " " << maxGood;

}

7. 
   Ответ: 1568 7935
   

Ещё пример задания:

Р-00. Рассматривается множество целых чисел, принадлежащих отрезку [1033; 7737], которые делятся на 5 и не делятся на 11, 17, 19 и 23. Найдите количество таких чисел и максимальное из них. В ответе запишите два числа через пробел: сначала количество, затем максимальное число.

Решение (простой перебор):

9. 
   поскольку заданный отрезок [1033; 7737] содержит не так много чисел, можно решать задачу простым перебором, особо не заботясь об эффективности вычислений
   
10. 
    условие будем понимать так: интересующие нас числа делятся на 5 и не делятся ни на одно из чисел 11, 17, 19 и 23
    
11. 
    нам выгоднее перебирать числа в порядке возрастания, тогда последнее найдённое число – это и есть искомое максимальное подходящее число (если требуется найти наименьшее подходящее число, удобнее перебирать числа в порядке убывания)
    
12. 
    полная программа на языке Python:
    

count = 0

maxGood = 0

for n in range(1033, 7737+1):

if (n % 5 == 0) and (n % 11 != 0) and \

(n % 17 != 0) and (n % 19 != 0) and (n % 23 != 0):

maxGood = n

count += 1

print(count, maxGood)

13. 
    ещё один вариант программы (с функцией):
    

def isGood(n):

return (n % 5 == 0) and (n % 11 != 0) and \

(n % 17 != 0) and (n % 19 != 0) and (n % 23 != 0)

count = 0

maxGood = 0

for n in range(1033, 7737+1):

if isGood(n):

maxGood = n

count += 1

print(count, maxGood)

14. 
    (Б.С. Михлин) на языке Python существует короткое решение, использующее генератор списка:
    

# В списке (массиве) "a" только нужные числа:

a = [n for n in range(1033,7737+1)

if (n%5==0 and n%11!=0 and n%17!=0 and

n%19!=0 and n%23!=0)]

print(len(a),max(a)) # max(a) можно заменить на a[-1]

# (последний элемент списка "a")

15. 
    Ответ: 1040 7730
    

Решение (программа на языке Pascal):

3. 
   аналогичная программа на языке Pascal:
   

var count, n, maxGood: integer;

begin

count:= 0;

maxGood:= 0;

for n:=1033 to 7737 do

if (n mod 5 = 0) and (n mod 11 <> 0) and

(n mod 17 <> 0) and (n mod 19 <> 0) and

(n mod 23 <> 0) then begin

maxGood:= n;

count := count + 1

end;

writeln(count, ' ', maxGood)

end.

4. 
   вариант с функцией:
   

var count, n, maxGood: integer;

function isGood(n: integer): boolean;

begin

isGood := (n mod 5 = 0) and (n mod 11 <> 0) and

(n mod 17 <> 0) and (n mod 19 <> 0) and

(n mod 23 <> 0);

end;

begin

count:= 0;

maxGood:= 0;

for n:=1033 to 7737 do

if isGood(n) then begin

maxGood:= n;

count:= count + 1

end;

writeln(count, ' ', maxGood)

end.

5. 
   Ответ: 1040 7730
   

Решение (программа на языке C++):

1. 
   аналогичная программа на языке C++:
   

#include

int main()

{

int count = 0;

int maxGood = 0;

for(int n=1033; n<=7737; n++)

if( (n % 5 == 0) and (n % 11 != 0) and

(n % 17 != 0) and (n % 19 != 0) and (n % 23 != 0) ) {

maxGood = n;

count += 1;

}

std::cout << count << " " << maxGood;

}

2. 
   вариант с функцией:
   

#include

bool isGood( int n )

{

return (n % 5 == 0) and (n % 11 != 0) and

(n % 17 != 0) and (n % 19 != 0) and (n % 23 != 0);

}

int main()

{

int count = 0;

int maxGood = 0;

for(int n=1033; n<=7737; n++)

if( isGood(n) ) {

maxGood = n;

count += 1;

}

std::cout << count << " " << maxGood;

}

3. 
   Ответ: 1040 7730
   

Решение (электронные таблицы Excel, Б.С. Михлин):

1. 
   введём в ячейку A1 первое число в заданном интервале кратное пяти 1035: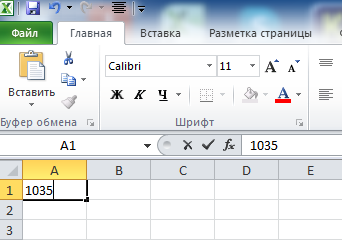
   

2. 
   заполним ряд натуральных чисел до конечного числа с шагом пять; на вкладке Главная выберем команду Прогрессия (используем идею И.В. Степанова):
   

3. 
   введём шаг равный пяти, заданное конечное значение 7737 (можно 7735) и отмечаем заполнение по столбцам (тип прогрессии арифметическая ‑ стоит по умолчанию):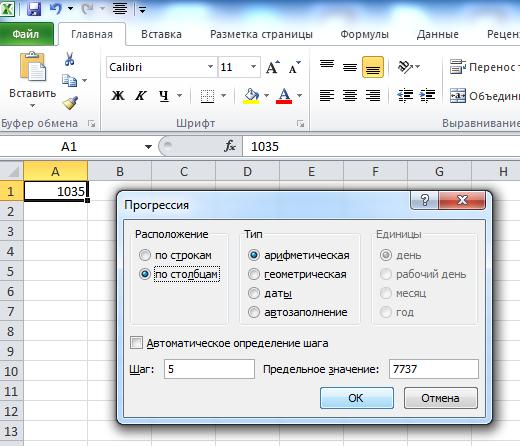
   

Колонка A заполнится арифметической прогрессией от 1035 до 7735 с шагом 5. Все эти числа кратны пяти и нам остается среди них отобрать в колонку B те числа, которые не кратны 11, 17, 19 и 23.

Примечание: Для быстрого перехода в начало (левый верхний угол) и в конец (правый нижний угол) заполненного блока ячеек удобно пользоваться комбинациями клавиш Ctrl+Home и Ctrl+End.

4. 
   в ячейку B1 введем следующую формулу: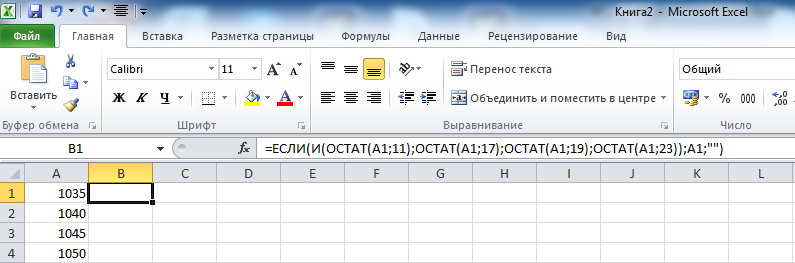
   

Если число в A1 не делятся на 11, 17, 19 и 23, то их остатки отличные от нуля будут рассматриваться логической операцией И, как ИСТИНА. Если все остатки будут отличны от нуля, то команда ЕСЛИ скопирует в ячейку колонки B число из колонки A. Если хотя бы один из остатков будет равен нулю, то он будет рассматриваться, как ЛОЖЬ и в ячейке колонки B будет пусто (пустая текстовая строка).

5. 
   двойным щелчком по маркеру заполнения (черный квадратик в правом нижнем углу ячейки B1) скопируем формулу на весь столбец B (пока не кончатся данные в столбце A).
   

Можно также взявшись за маркер заполнения B1 тащить (копировать) формулу вниз, но так будет гораздо дольше.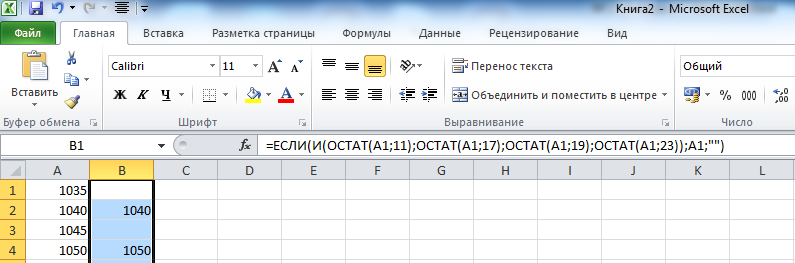

6. 
   в столбце B мы видим только те числа, которые удовлетворяют всем условиям задачи. Не снимая выделение с чисел колонки B, посчитаем их количество (команды Сумма (Σ) - Число):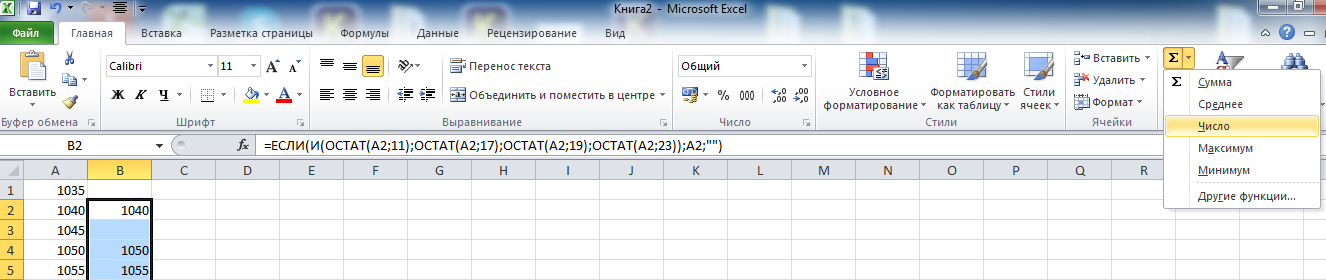
   

Переходим вниз чисел в колонке B (Ctrl+End) и видим количество чисел 1040 и максимальное число 7730.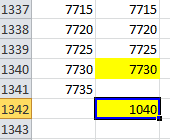

7. 
   Ответ: 1040 7730