Перегудов Ф. И., Тарасенко Ф. П
 Скачать 4.17 Mb. Скачать 4.17 Mb.
|
§ 3.7. ДИНАМИЧЕСКИЕ МОДЕЛИ СИСТЕМДо сих пор основное внимание было уделено понятию системы, ее составу и устройству. Были построены модели, которые являются как бы “фотографиями” системы, отображают ее в некоторый момент времени. В этом смысле рассмотренные варианты моделей “черного ящика”, состава, структуры и структурной схемы системы могут быть названы статическими моделями, что подчеркивает их неподвижный, как бы застывший характер. ОТОБРАЖЕНИЕ ДИНАМИКИ СИСТЕМЫ Следующий шаг в исследовании систем состоит в том, чтобы понять и описать, как система “работает”, что происходит с ней самой и с окружающей средой в ходе реализации поставленной цели. Очевидно, и подход к описанию, и степень подробности описания происходящих процессов могут быть различными. Однако общим при этом является то, что разрабатываемые модели должны отражать поведение систем, описывать происходящие с течением времени изменения, последовательность каких-то этапов, операций, действий, причинно-следственные связи. Системы, в которых происходят какие бы то ни было изменения со временем, будем называть динамическими, а модели, отображающие эти изменения, – динамическими моделями систем. Заметим, что термин “динамический” в русском языке неоднозначен; здесь он будет использован в самом широком смысле как обозначение любых изменений во времени. Для разных объектов и систем разработано большое количество динамических моделей, описывающих процессы с различной степенью детальности: от самого общего понятия динамики, движения вообще, до формальных математических моделей конкретных процессов типа уравнений движения в механике или волновых уравнений в теории поля. Развитие моделей происходит примерно в той последовательности, как это было изложено: от “черного ящика” к “белому”. Однако этот путь конкретизации моделей непрост и нелегок и для многих систем еще не закончен из-за недостаточности имеющихся знаний. ФУНКЦИОНИРОВАНИЕ И РАЗВИТИЕ Уже на этапе “черного ящика” различают два типа динамики системы: ее функционирование и развитие. Под функционированием подразумевают процессы, которые происходит в системе (и окружающей ее среде), стабильно реализующей фиксированную цель (функционируют, например, часы, городской транспорт, кинотеатр, канцелярия, радиоприемник, станок, школа и т.д.). Развитием называют то, что происходит с системой при изменении ее целей. Характерной чертой развития является тот факт, что существующая структура перестает соответствовать новой цели, и для обеспечения новой функции приходится изменять структуру, а иногда и состав системы, перестраивать всю систему*. Не следует считать, что система всегда находится либо в фазе развития, либо в состоянии функционирования. При реконструкции одного цеха остальные функционируют, завод в целом развивается. Даже при коренной перестройке системы какие-то элементы и даже подсистемы старой структуры могут продолжать функционировать в новой по-прежнему. Возможны и такие системы, для функционирования которых какие-то ее подсистемы должны быть постоянно в развитии. Следующий шаг в построении динамических моделей состоит в том, чтобы конкретнее отобразить происходящие изменения. Это означает, что следует различать части, этапы происходящего процесса, рассматривать их взаимосвязи. Иными словами, типы динамических моделей такие же, как и статических, только элементы этих моделей имеют временной характер. Например, динамический вариант “черного ящика” – указание начального (“вход”) и конечного (“выход”) состояний системы (например, как в пятилетнем плане). Модели состава соответствует перечень этапов в некоторой упорядоченной последовательности действий. Например, доказано, что любой алгоритм можно построить, используя всего три оператора: “выполнять последовательно”, “если... то...” и “выполнять, пока не удовлетворится условие”. Эти операторы можно рассматривать как модель минимального состава алгоритма, хотя не обязательно составлять алгоритм только из этих операторов. Динамический вариант “белого ящика” – это подробное описание происходящего или планируемого процесса. Например, на производстве широко используют так называемые сетевые графики – графы, имеющие сетевую структуру; их вершинами служат выполняемые производственные операции, а ребра указывают, какие операции не могут начаться, пока не окончатся предыдущие. Здесь же некоторым образом (например, с помощью задания длин или весов ребер) изображается длительность выполнения операций, что и позволяет находить на графе “критические” пути, т.е. последовательности операций, от которых главным образом зависит ритмичность всей работы. ТИПЫ ДИНАМИЧЕСКИХ МОДЕЛЕй Те же типы моделей прослеживаются и при более глубокой формализации динамических моделей [4]. При математическом моделирований некоторого процесса его конкретная реализация описывается в виде соответствия между элементами множества Х возможных “значений” х и элементов упорядоченного множества Т “моментов времени” t, т.е. в виде отображения TX: x(t) XT, tT. С помощью этих понятий можно строить математические модели систем. Рассматривая выход у(t) системы (это может быть вектор) как ее реакцию на управляемые u(t) и неуправляемые v(t) входы х(t) = { u(t), v(t) } (рис. 3.7), можно модель “черного ящика” выразить как совокупность двух процессов: ХT= {х(t)} и YT={у(t)}, tT. Если даже считать у(t) результатом некоторого преобразования процесса х(t), т.е. у(t) = (х(t)), то модель “черного ящика” предполагает, что это преобразование неизвестно. В том же случае, когда мы имеем дело с “белым ящиком”, соответствие между входом и выходом можно описать тем или иным способом. Какой именно способ – зависит от того, что нам известно, и в какой форме можно использовать эти знания.  3.7 ————— Динамическая модель “черного ящика”: задание процессов на входах и выходах системы Например, иногда бывает известно, что система мгновенно преобразует вход в выход, т.е. что у(t) является функцией только х(t) в тот же момент времени. Остается задать или найти эту функцию. На практике чаще всего известна лишь безынерционность системы и требуется, наблюдая входы и выходы, восстановить неизвестную функцию у = (х). По существу, это задача о переходе от модели “черного ящика” к модели “белого ящика” по наблюдениям входов и выходов при наличии информации о безынерционности системы. Даже в такой достаточно простой постановке задача имеет совсем не простые варианты, которые зависят от того, что известно о функции (в параметризованном случае принадлежит семейству функций, известных с точностью до параметров; в непараметризованном – вид функции неизвестен), и от наличия или отсутствия некоторых общих сведений о ее свойствах (непрерывности, гладкости, монотонности, симметричности и т.п.). Дополнительные варианты (и дополнительные трудности) возникают, если входы или выходы наблюдаются с помехами или искажениями. При этом разные предположения о природе этих помех приводят к принципиально отличающимся решениям задачи (например, в случае, когда распределение помехи известно точно, известно с точностью до числовых параметров или неизвестно совсем). Однако класс систем, которые можно считать безынерционными, весьма узок. Необходимо строить математические модели систем, выход которых определяется не только значением входа в данный момент времени, но и теми значениями, которые были на входе в предыдущие моменты. Более того, в самой системе с течением времени как под влиянием входных воздействий, так и независимо от них могут происходить изменения, что также следует отразить в модели. ОБЩАЯ МАТЕМАТИЧЕСКАЯ МОДЕЛЬ ДИНАМИКИ В наиболее общей модели [2; 4] это достигается введением понятия состояния системы как некоторой (внутренней) характеристики системы, значение которой в настоящий момент времени определяет текущее значение выходной величины. Состояние можно рассматривать как своего рода хранилище информации, необходимой для предсказания влияния настоящего на будущее [1, с. 12 – 13]. Обозначим это состояние через z(t). Все сказанное выше означает существование такого отображения : ZТY, что y(t) = (t, z(t)), tT. (1) Явная зависимость от t введена для учета возможности изменения зависимости выхода от состояния с течением времени. Это отображение называется отображением выхода. Для завершения построения модели нужно описать связь между входом и состоянием, т.е. ввести параметрическое семейство отображений t : ZX(·)Z, заданных для всех значений параметров tT, T и t. Это означает принятие аксиомы о том, что состояние в любой момент t > однозначно определяется состоянием z в момент и отрезком реализации входа х (·) от до t: z(t) = t(z?, x()) = ??(t; ?, z?, x()). (2) Такое отображение называют переходным отображением. Итак, математическая модель системы, соответствующая уровню “белого ящика”, – это задание множеств входов, состояний и выходов, и связей между ними: Конкретизируя множества Х, Z и Y и отображения и , можно перейти к моделям различных систем. Так, говорят о дискретных и непрерывных по времени системах в зависимости от того, дискретно или непрерывно множество Т. Далее, если множества Х, Z и Y дискретной по времени системы имеют конечное число элементов, то такую систему называют конечным автоматом. Это довольно простой класс систем в том смысле, что для исследования конечных автоматов необходимы лишь методы логики и алгебры; в то же время это широкий и практически важный класс, так как в него входят все дискретные (цифровые) измерительные, управляющие и вычислительные устройства, в том числе и ЭВМ. VERTEX вершина (графа) ARC дуга (графа) LINEAR линейный STATE состояние FUNCTION функция Объединив модели “черного ящика”, состава и структуры системы, мы получим самую полную (для наших целей), самую подробную (для нашего уровня знаний) модель системы – ее структурную схему. Модели, отображающие процессы, происходящие в системе с течением времени. называются динамическими моделями. Динамические модели включают те же типы, что и статические, но с явным выделением, подчеркиванием роли времени. Всякая реальная динамическая система подчинена принципу причинности: отклик не может появиться раньше стимула. Условия, при которых модель отражает этот принцип, называются условиями физической реализуемости модели; нахождение этих условий часто является нетривиальной задачей. Если Х, Z и Y – линейные пространства, а и – линейные операторы, то и система называется линейной*. Если к линейной системе дополнительно предъявить требования, состоящие в том, чтобы пространства имели топологическую структуру**, а и были бы непрерывны в этой топологии, то мы приходим к гладким системам. Этот класс систем имеет большое значение, так как оказалось [2], что для гладких систем переходное отображение является общим решением дифференциального уравнения а для дискретных систем – общим решением уравнения где х(·) – траектория для моментов времени ttk. Интенсивно исследовались стационарные системы, т.е. такие системы, свойства которых со временем не изменяются. Стационарность означает независимость от t функции и инвариантность функции к сдвигу во времени: гдеx(·) есть х(·), сдвинутое на время . —————————— * Основным свойством линейных систем является выполнение принципа суперпозиции, т. е. условия [х(t)=х1(t) + +х2(t)] [у(t)=у1(t)+у2(t)], где х1(t) и х2(t) – некоторые входные воздействия, а у1(t) и у2(t) – выходные отклики на каждый из них в отдельности. ** Не вдаваясь в математические подробности, отметим, что задание топологической структуры множества позволяет строго определить основные понятия анализа на этом множестве, например сходимость последовательностей на нем, а также вводить метрику (меру близости между элементами пространства). Конкретизация моделей динамических систем на этом, конечно, не заканчивается; приведенные модели скорее всего являются просто примерами, которые можно рассматривать отдельно. Но на одном свойстве реальных динамических систем следует остановиться. Речь идет о подчиненности реальных систем принципу причинности. Согласно этому принципу, отклик системы на некоторое воздействие не может начаться раньше самого воздействия. Это условие, очевидное для реальных систем, совсем не автоматически выполняется в рамках их математических моделей. При этом модель, в которой нарушается принцип причинности, не обязательно является “плохой”, бесполезной. Примером служит модель фильтра с конечной полосой пропускания: отклик такой системы на короткий импульс имеет вид sin0t/(0t), т.е. начинается в минус бесконечности. Несмотря на явное нарушение принципа причинности, такую модель широко используют в радиотехнике. Однако, как только возникает вопрос о практической реализации такого фильтра, становится ясно, что она невозможна в точном смысле, хотя допустимы различные приближения. В связи с этим одна из проблем теории динамических систем состоит в выяснении условий физической реализуемости теоретических моделей, т.е. конкретных ограничений, которые приходится накладывать на модель при соблюдении принципа причинности.
ЗАКЛЮЧЕНИЕОказывается, что при всем невообразимом многообразии реальных систем принципиально различных типов моделей систем очень немного: модель типа “черный ящик”, модель состава, модель структуры, а также их разумные сочетания и прежде всего объединение всех трех моделей, т.е. структурная схема системы. Это относится как к статическим моделям, отображающим фиксированное состояние системы (рис. 3.8, а), так и к динамическим моделям, отображающим характер временных процессов, которые происходят с системой (рис. 3.8, б). Рис. 3.8 иллюстрирует общность типов статических и динамических моделей. Можно сказать, что структурная схема (“белый ящик”) получается как результат “суммирования” моделей “черного ящика”, состава и структуры системы. Все указанные типы моделей являются формальными, относящимися к любым системам и, следовательно, не относящимися ни к одной конкретной системе. Чтобы получить модель заданной системы, нужно придать формальной модели конкретное содержание, т.е. решить, какие аспекты реальной системы включать как элементы модели избранного типа, а какие – нет, считая их несущественными. Этот процесс, как было показано, обычно неформализуем, поскольку признаки существенности или несущественности в очень редком случае удается формализовать (к таким случаям относится, например, возможность принять в качестве признака существенности частоту встречаемости данного элемента в различных подобных, т. е. одинаково классифицируемых, системах). Столь же слабо формализованными являются признаки элементарности и признаки разграничения между подсистемами. В силу указанных причин, процесс построения содержательных моделей является процессом интеллектуальным, творческим. Тем не менее интуиции эксперта, разрабатывающего содержательную модель, немало помогают формальная модель и рекомендации по ее наполнению конкретным содержанием. Формальная модель является “окном”, через которое эксперт смотрит на реальную систему, строя содержательную модель. В процессе построения содержательных моделей систем отчетливо прослеживается необходимость использования диалектики. В этом процессе главной является задача создания полной модели. Общие рекомендации по достижению полноты вытекают из основных положений диалектики: 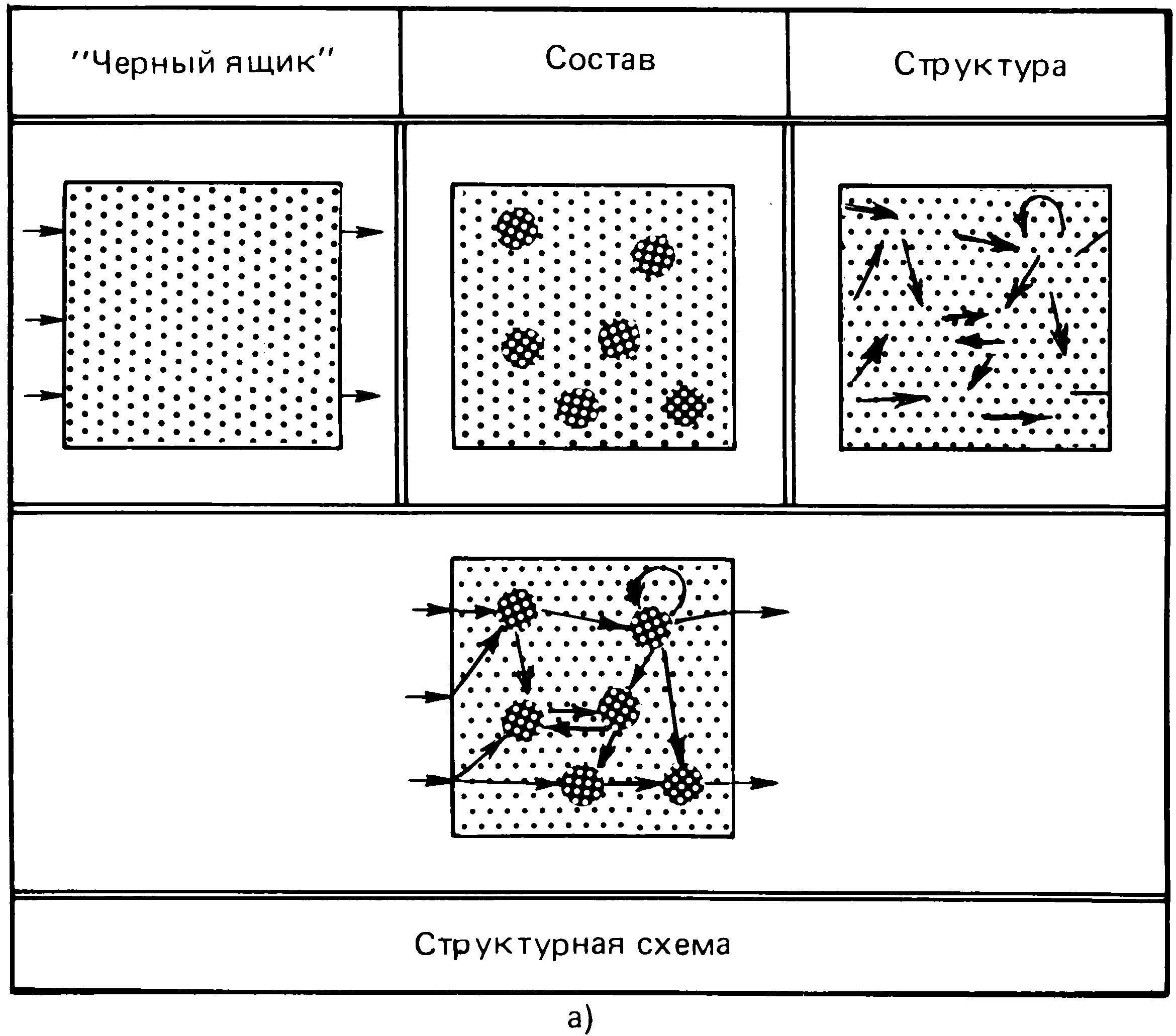 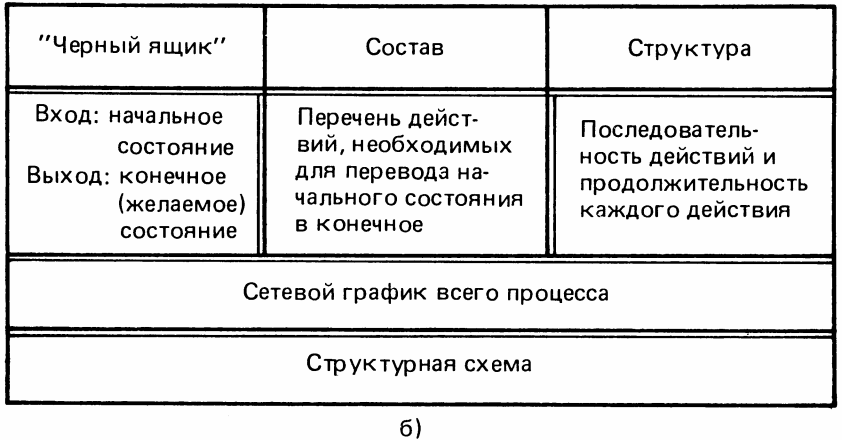 3.8 ————— Типы моделей: а) статический вариант; б) динамический вариант необходимо стремиться учесть все существенные факторы, влияющие на рассматриваемое явление; поскольку такая существенность не всегда очевидна, лучше включить в модель несущественный элемент, чем не включить существенный; одним из необходимых признаков полноты модели является наличие в ней противоречивых элементов; следует уделить специальное внимание этому моменту: например, при перечислении выходов надо включать в перечень не только желательные целевые выходы (связи, продукцию и т.п.), но и нежелательные (отходы, брак, и т.п.); как бы ни были обширны наши знания о данном явлении, реальность богаче моделей – в ней всегда есть неизвестные факторы; чтобы не упустить из виду возможность чего-то существенного, но пока неизвестного, рекомендуется включать в модель неявные “запасные”, неконкретизированные элементы (типа “все остальное”, “что-то еще”) и на различных стадиях системного анализа обращаться к этим элементам, как бы ставя перед собой вопрос: не пора ли дополнить модель еще одним явным элементом? Эти рекомендации, конечно, не исчерпывают всех возможностей: в арсенал искусства моделирования входит много научно обоснованных методов и эмпирических эвристик (см., например, [1; 3; 9]). ЛИТЕРАТУРА
УПРАЖНЕНИЯ3.2
а) системы, которая предназначена для выполнения определенной цели, но которую можно использовать и для других целей; б) системы, спроектированной специально для реализации одновременно нескольких различных целей; в) разных систем, предназначенных для одной и той же цели.
§ 3.3
§ 3.4
§ 3.5
§ 3.6
§ 3.7
Вопросы |
Искусственные | Глава четвертая |
