|
|
Перегудов Ф. И., Тарасенко Ф. П
§ 3.6. ВТОРОЕ ОПРЕДЕЛЕНИЕ СИСТЕМЫ.
СТРУКТУРНАЯ СХЕМА СИСТЕМЫ
Объединяя все изложенное в предыдущих параграфах, можно сформулировать второе определение системы: система есть совокупность взаимосвязанных элементов, обособленная от среды и взаимодействующая с ней как целое.
СТРУКТУРНАЯ СХЕМА КАК СОЕДИНЕНИЕ МОДЕЛЕЙ
Очевидно, что это определение охватывает модели “черного ящика”, состава и структуры. Все вместе они образуют еще одну модель, которую будем называть структурной схемой системы; в литературе встречаются также термины “белый ящик”, “прозрачный ящик”, подчеркивающие ее отличие от модели “черного ящика”, а также термин “конструкция системы”, который мы будем использовать для обозначения материальной реализации структурной схемы системы. В структурной схеме указываются все элементы системы, все связи между элементами внутри системы и связи определенных элементов с окружающей средой (входы и выходы системы).
Пример 1. Структурная схема системы “синхронизируемые часы” приведена на рис. 3.3. Элементы системы изображены в виде прямоугольников; связи 1 – 3 между элементами описаны в примере 3 § 3.5; вход 4 изображает поступление энергии извне; вход 5 соответствует регулировке индикатора; выход 6 – показание часов.

3.3
—————
Структурная схема часов
Все структурные схемы имеют нечто общее, и это побудило математиков рассматривать их как особый объект математических исследований. Для этого пришлось абстрагироваться от содержательной стороны структурных схем, оставив в рассматриваемой модели только общее для каждой схемы. В результате получилась схема, в которой обозначается только наличие элементов и связей между ними, а также (в случае необходимости) разница между элементами и между связями. Такая схема называется графом. Следовательно, граф состоит из обозначений элементов произвольной природы, называемых вершинами, и обозначений связей между ними, называемых ребрами (иногда дугами). На рис. 3.4 изображен граф: вершины обозначены в виде кружков, ребра – в виде линий. Часто бывает необходимо отразить несимметричность некоторых связей; в таких случаях линию, изображающую ребро, снабжают стрелкой. Если направления связей не обозначаются, то граф называется неориентированным, при наличии стрелок – ориентированным (полностью или частично). Данная пара вершин может быть соединена любым количеством ребер; вершина может быть соединена сама с собой (тогда ребро называется петлей). Если в графе требуется отразить другие различия между элементами или связями, то либо приписывают разным ребрам различные веса (взвешенные графы), либо раскрашивают вершины или ребра (раскрашенные графы).
Оказалось, что для графов может быть построена интересная и содержательная теория, имеющая многочисленные приложения. Разнообразные задачи этой теории связаны с различными преобразованиями графов, а также с возможностью рассмотрения различных отношений на графах: весов, рангов, цветов, вероятностных характеристик (стохастические графы) и т.д. В связи с тем что множества вершин и ребер формально можно поменять местами, получается два разных представления системы в виде вершинного или в виде реберного графа. Оказывается, что в одних задачах удобнее использовать вершинный, а в других – реберный граф [6].
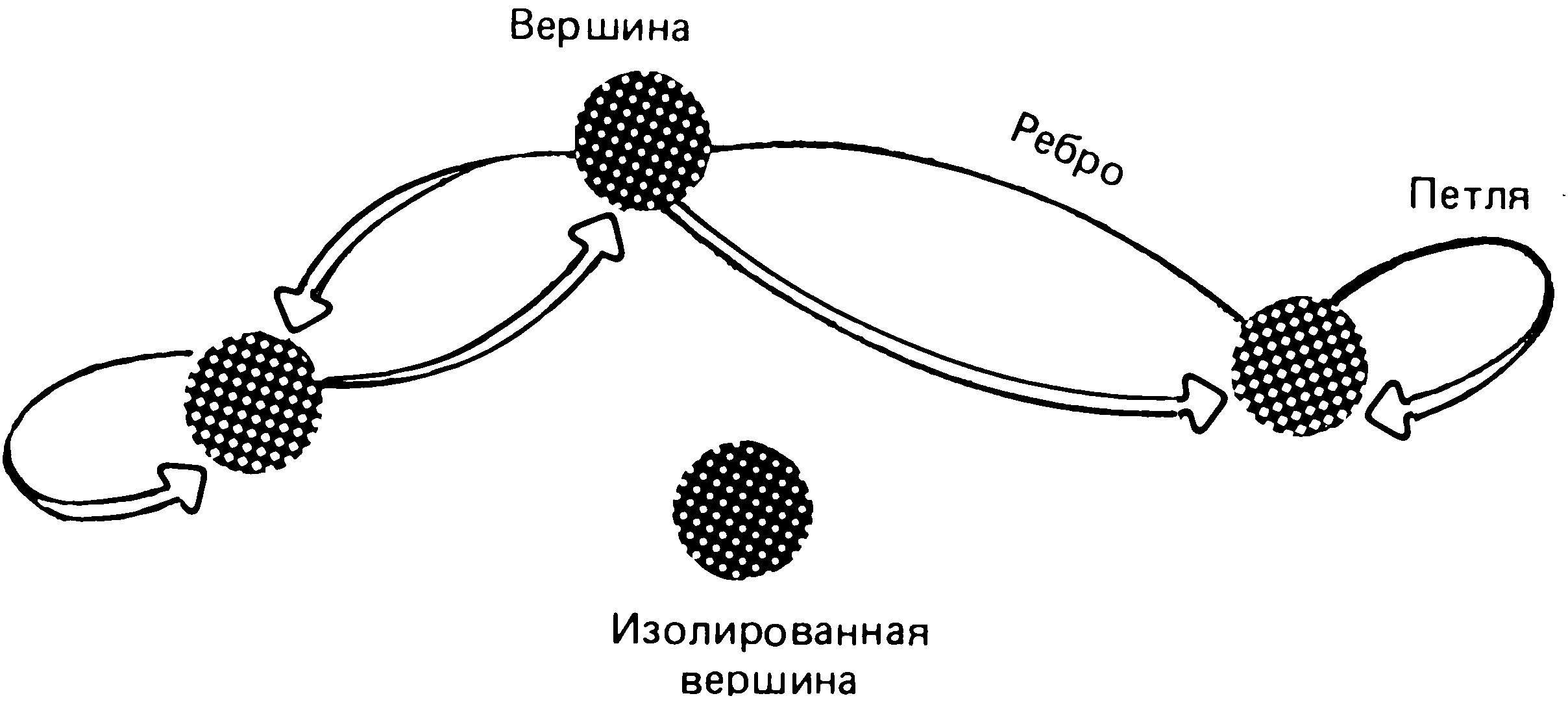
3.4
—————
Пример графа
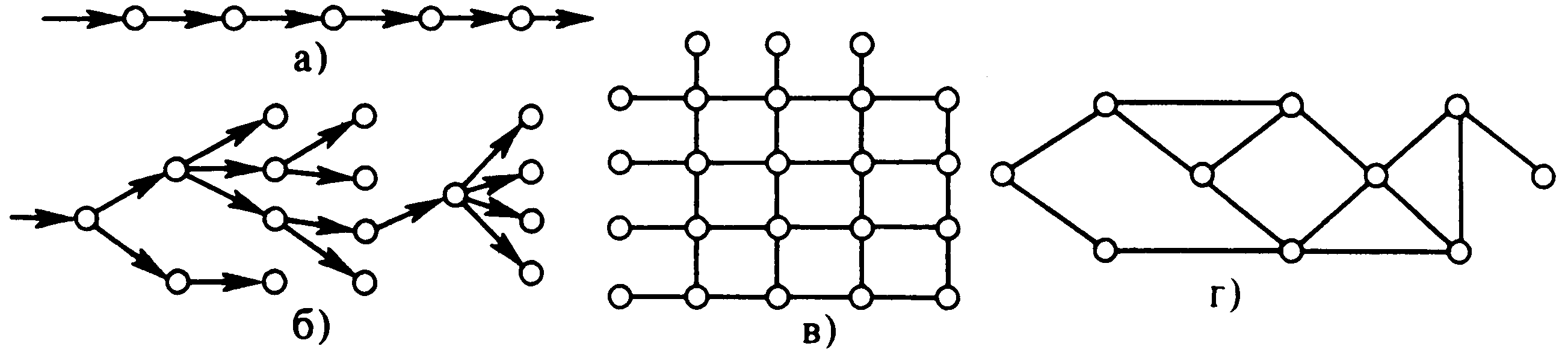
3.5
—————
Графы, соответствующие различным структурам: а) линейная структура; б) древовидная структура; в) матричная структура; г) сетевая структура
Графы могут изображать любые структуры, если не накладывать ограничений на пересекаемость ребер. Некоторые типы структур имеют особенности, важные для практики, они выделены из других и получили специальные названия. Так, в организационных системах часто встречаются линейные, древовидные (иерархические) и матричные структуры; в технических системах чаще встречаются сетевые структуры (рис. 3.5); особое место в теории систем занимают структуры с обратными связями, которые соответствуют кольцевым путям в ориентированных графах (такие структуры будут рассмотрены отдельно).
Пример 2. Структурная схема ЭВМ пятого поколения, с помощью которой пользователь, не умеющий программировать, может решать достаточно сложные задачи [7], приведена на рис. 3.6. Отметим, что в этой схеме имеются и иерархические, и линейные, и обратные связи.
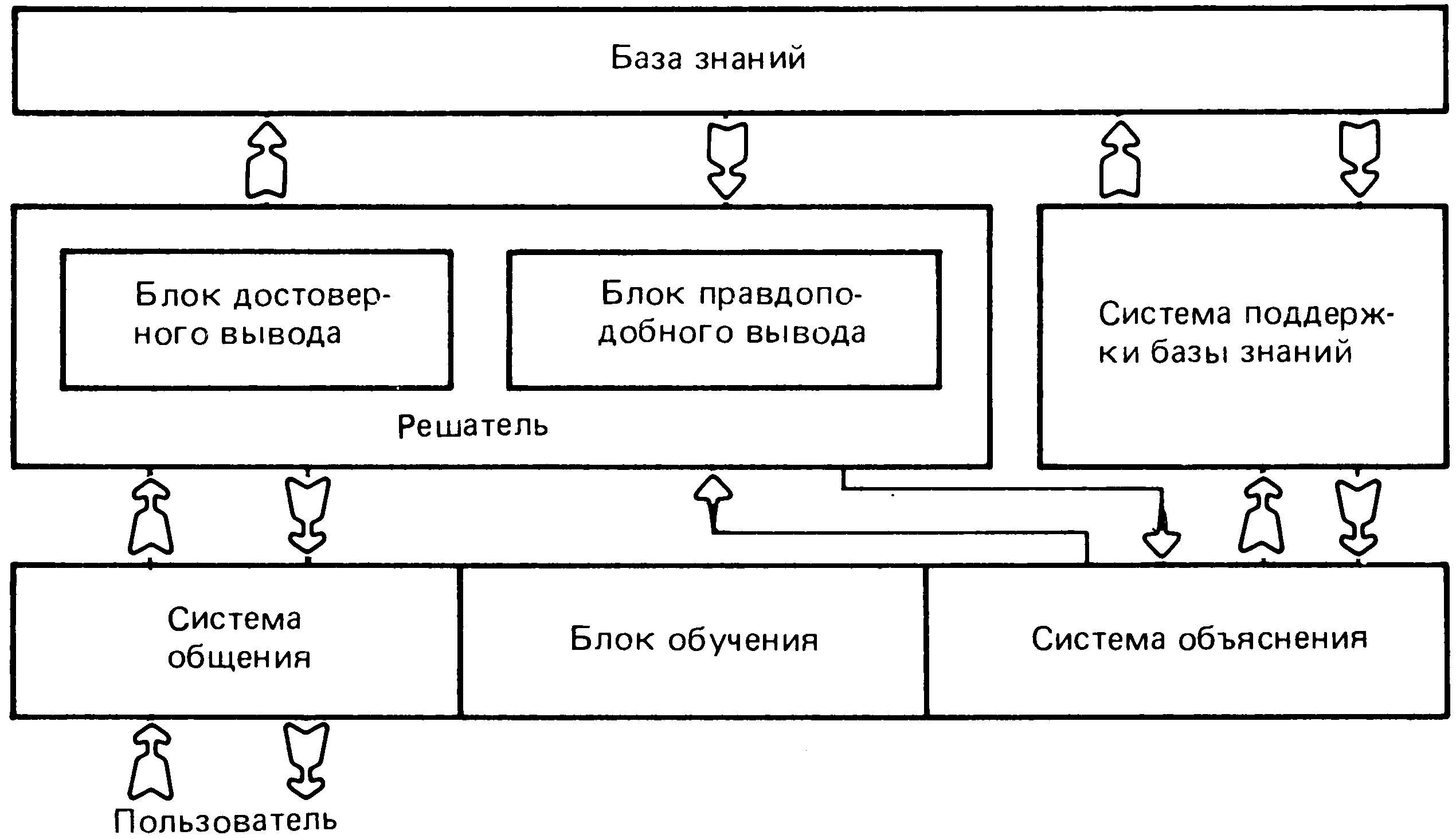
3.6
—————
Структурная схема ЭВМ пятого поколения
Одной структурной информации, которая содержится в графах, для ряда исследований недостаточно. В таких случаях методы теории графов становятся вспомогательными, а главным является рассмотрение конкретных функциональных связей между входными, внутренними и выходными переменными системы.
Подведем итог
Структурная схема системы является наиболее подробной и полной моделью любой системы на данном этапе нашего познания. При этом остается актуальным вопрос об адекватности этой модели, разрешаемый только на практике.
|
Summary
The structural scheme of a system is the most detailed and exhaustive model of any system at a given stage of our knowledge. The problem of the adequacy of the model still exists, and can be solved only in practice.
| |
|
|
 Скачать 4.17 Mb.
Скачать 4.17 Mb.



